यूक्लिड की ज्यामिति का परिचय कक्षा 9 गणित
MOTIVATION
हैलो बच्चों !
स्वागत है आप सभी का कक्षा -9 वीं के पाँचवें अध्याय यूक्लिड की ज्यामिति का परिचय में।
मैं आशा करता हूँ कि इन notes को पढ़कर आपको मजा आएगा और साथ ही साथ आपके सभी Concept भी clear हो जायेंगे।
इन notes में उन सभी concept को आसान भाषा में समझाया गया है जिनका प्रयोग आपको परीक्षा में प्रश्नों को हल करने में करना होगा
साथ ही साथ इस अध्याय के concepts का प्रयोग आपको class-10 में भी करना होगा, इसलिए सभी बिंदुओं को आप बहुत ध्यान से पढ़ें और उनसे संबंधित प्रश्नों को हल करे।
भूमिका
बच्चों, शब्द 'ज्यामिति' (geometry) यूनानी भाषा के शब्दों 'जियो' (geo) और 'मीट्रीन' (metrein) से मिल कर बना है। जियो का अर्थ है 'पृथ्वी' या 'भूमि' और मीट्रीन का अर्थ है 'मापना'। इससे ऐसा प्रतीत होता है कि ज्यामिति का उद्गम भूमि मापने की आवश्यकता के कारण हुआ है। विभिन्न देशों के लोगों को अनेक व्यावहारिक समस्याओं का सामना करना पड़ा जिनमें ज्यामिति के विकास की विभिन्न प्रकार से आवश्यकता पड़ी।
उदाहरण के तौर पर, जब भी नील नदी में बाढ़ आती थी, तो विभिन्न भूमि स्वामियों के संलग्न खेतों के बीच की परिसीमाओं (boundaries) को अपने साथ बहा ले जाती थी। इन बाढ़ों के बाद, इन परिसीमाओं को पुनः बनाया जाता था। इस कार्य के लिए, मिस्रवासियों ने सरल क्षेत्रफल परिकलित करने के साथ ही सरल रचनाएँ करने के लिए, अनेक ज्यामितीय तकनीकें और नियम विकसित किए। उन्होंने ज्यामिति के ज्ञान का उपयोग अन्नभण्डारों के आयतन निकालने तथा नहरों और पिरामिडों (pyramids) के निर्माण करने में किया। वे एक कटे हुए पिरामिड (truncated pyramid) आकृति 5.1 : कटा हुआ पिरामिड (देखिए आकृति 5.1) का आयतन ज्ञात करने का सूत्र भी जानते थे | हम जानते हैं कि पिरामिड एक ऐसी ठोस आकृति होती है , जिसका आधार एक त्रिभुज या वर्ग या कोई अन्य बहुभुज होता है और पार्श्व फलक ऊपर एक ही बिन्दु पर मिलने वाले त्रिभुज होते हैं |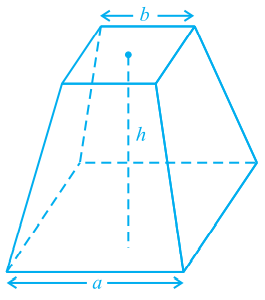
एक यूनानी गणितज्ञ थेल्स (Thales) को श्रेय जाता है कि उन्होंने सबसे पहली ज्ञात उपपत्ति (proof) प्रदान की। यह उपपत्ति इस कथन की थी कि वृत्त का व्यास वृत्त को समद्विभाजित (अर्थात् दो बराबर भागों में विभाजित) करता है। थेल्स का एक सबसे प्रसिद्ध शिष्य पाइथागोरस था, जिसका नाम आपने अवश्य सुना होगा। पाइथागोरस और उसके साथियों ने अनेक ज्यामितीय गुणों की खोज की और ज्यामिति के सिद्धांतों का अत्याधिक विकास किया। यह प्रक्रिया 300 ई०पू० तक जारी रही। इसी समय मिस्र में अलेक्जेंड्रिया के एक गणित के शिक्षक यूक्लिड (Euclid) ने उस समय तक ज्ञात गणित के सभी ज्ञान को एकत्रित किया और एलीमेंट्स (Elements) नामक अपने प्रसिद्ध ग्रंथ के रूप में उसे व्यवस्थित किया। उन्होंने एलीमेंट्स को 13 अध्यायों में विभाजित किया, जिनमें से प्रत्येक को 'पुस्तिका' माना जाता है।
यूक्लिड इन पुस्तिकाओं ने समस्त विश्व की ज्यामिति संबंधी समझ को आने वाली पीढ़ियों तक प्रभावित किया।
इस अध्याय में, हम ज्यामिति के प्रति यूक्लिड के दृष्टिकोण की चर्चा करेंगे और ज्यामिति के वर्तमान स्वरूप से इसे जोड़ने का प्रयत्न करेंगे।
यूक्लिड की परिभाषाएँ
आकाश और उनके आस-पास के ठोसों के अध्ययनों के आधार पर , एक ठोस वस्तु की सिद्धांतीय ज्यामिति अवधारणा विकसित की गई | यूक्लिड ने गहन अध्ययन करके इन ठोसों से सम्बन्धित कुछ परिभाषाएं दीं जो ठोस आकृति से सम्बन्धित थीं | क्योंकि एक ठोस का आकार होता है , माप और स्थिति होती है तथा उसे एक स्थान से दूसरे स्थान पर ले जाया जा सकता है | ठोस की परिसीमाएँ पृष्ठ (Surface) कहलाती हैं |
ज्यामिति से सम्बन्धित यूक्लिड ने निम्न तथ्य दिए
यूक्लिड की परिभाषाएँ:
यूक्लिड की अभिधारणाएँ एवं अभिगृहीत
यूक्लिड ने कुछ गुणों को बिना सिद्ध किए सत्य कथन मानने की कल्पना की। ये कल्पनाएँ वास्तव में 'स्पष्टतः सर्वव्यापी सत्य' थे।
यूक्लिड ने सामान्यतः इनको दो वर्गों अभिगृहीत (axioms) और अभिधारणाएँ (postulates) में विभाजित किया, जो निम्न हैं
अभिगृहीत (axioms)
अभिगृहीत (axioms) वे कल्पनाएँ थीं जिन्हें निरंतर गणित में प्रयोग किया गया और जिनका केवल ज्यामिति से ही विशेष संबंध नहीं था। इन्हे सामान्य अभिधारणाएँ भी कहते हैंअभिधारणाएँ (postulates)
अभिधारणा शब्द का प्रयोग उन कल्पनाओं के लिए किया जो विशिष्ट रूप से ज्यामिति से संबंधित थीं।अभिगृहीत
वे कल्पनाएँ, जिन्हें निरंतर गणित में प्रयोग किया गया और जिनका केवल ज्यामिति से ही विशेष संबंध नहीं था, अभिगृहीत होती हैं। इन्हे सामान्य अभिधारणाएँ भी कहते हैं
ये निम्नलिखित हैं
अभिधारणा : 1
एक बिंदु से एक अन्य बिंदु तक एक सीधी रेखा खींची जा सकती है।
यह अभिधारणा हमें बताती है कि दो भिन्न (distinct) बिंदुओं से होकर कम से कम एक रेखा अवश्य खींची जा सकती है, परन्तु इससे यह नहीं ज्ञात होता कि ऐसी एक से अधिक सीधी रेखाएँ नहीं हो सकतीं, अर्थात दो भिन्न बिंदुओं से एक अद्वितीय (unique) रेखा ही खींची जा सकती है। हम इस परिणाम को निम्न अभिगृहीत से समझ सकते हैं
अभिगृहीत 5.1
दिए हुए दो भिन्न बिंदुओं से होकर एक अद्वितीय रेखा खींची जा सकती है।
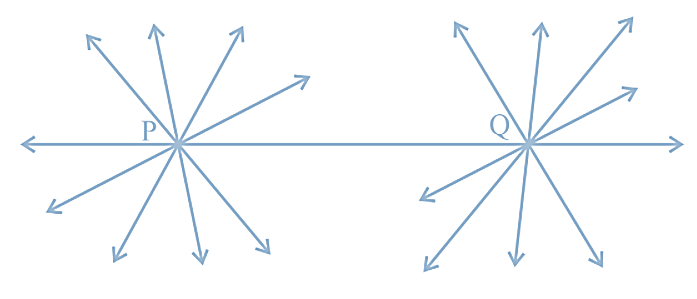
यहाँ चित्र मे देखिए दो बिन्दु P व Q है अगर इन बिन्दुओ से भिन्न दिशाओ मे भिन्न भिन्न रेखाये गुजारी जाए तो देखो की ऐसी कितनी रेखाएँ है जो बिंदु P से होकर खींची जा सकती हैं जो बिंदु Q से होकर भी जाती हों।
इसे आप किसी कागज मे भी करके देख सकते है।
आप पाएंगे की केवल एक रेखा PQ है, जो बिंदु P व Q दोनों से होकर जाती है और यह संयोग नहीं है ऐसा हर बार होगा जितने भी बार आप रेखायें खिचने का प्रयास करेंगे।
अतः हम कह सकते है की दिए हुए दो भिन्न बिंदुओं से होकर एक अद्वितीय रेखा खींची जा सकती है।
अभिधारणा : 2
एक सांत रेखा (terminated line) को अनिश्चित रूप से बढ़ाया जा सकता है
चूंकि जिसको हम वर्तमान में रेखाखंड (line segment) कहते हैं, उसे यूक्लिड ने सांत रेखा कहा था। अतः, दूसरी अभिधारणा यह कहती है कि एक रेखाखंड को दोनों ओर विस्तृत करके एक रेखा बनाई जा सकती है

अभिधारणा : 3
किसी बिंदु को केंद्र मानकर किसी त्रिज्या से एक वृत्त खींचा जा सकता है।
इसे समझने के लिए आप एक कागज ले जिस पर एक केंद्र बिन्दु ले अब इस पर अपना प्रकार की नोंक रखे अब किसी भी माप की त्रिज्या लेने के लिए प्रकार की नोंक और पेंसिल वाले भाग को फैला दें। माना 4 cm की त्रिज्या आप ले रहे है अब इस त्रिज्या से आप प्रकार की सहायता से एक वृत्त खिच सकते है परन्तु इसमे खास यह है की आप इस प्रकार का केवल एक वृत्त ही खिच पाएंगे।
अभिधारणा : 4
सभी समकोण (right angles) बराबर होते हैं।
जैसा की हम जानते है किन्ही दो लम्बवत रेखाओ के मध्य बना कोण समकोण कहलाता है, जिसका मान 90∘ होता है आप इसके बारे मे अगले अध्याय मे विस्तार से पढ़ेंगे। यहाँ से समझ आता है की चूंकि समकोण का मान 90∘ के बराबर होता है अतः सभी समकोण का मान आपस मे समान होता है।
अभिधारणा : 5
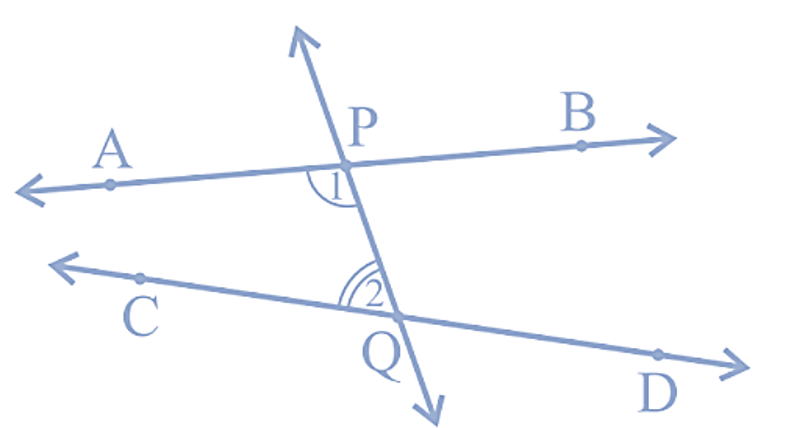
यदि एक सीधी रेखा दो सीधी रेखाओं पर इस प्रकार गिरे कि उसके एक ही ओर के दो अंतः कोणों (interior anglen) का योग दो समकोण (180∘) से कम हो, तो दोनों सीधी रेखाओं को अनिश्चित रूप से बढ़ाए जाने पर वे उसी ओर मिलती है जिस ओर दो कोणो का योग दो समकोणों से कम होता है।
इस अभिधारणा को निम्न उदहारण से समझ सकते हैं ,
रेखा PQ, रेखाओं AB और CD पर इस प्रकार गिरती है कि अंत: कोणों 1 और 2 का योग, जो PQ के बाईं ओर स्थित हैं, 180° से कम है। अत:, रेखाएँ AB और CD अंतत: PQ के बाईं ओर प्रतिच्छेद करेंगी।
OMR (One Minute Revision)
प्रमेय या साध्य
यूक्लिड ने अपनी अभिधारणाएँ और अभिगृहीतों को देने के बाद, इनका प्रयोग अन्य परिणामों को सिद्ध करने में किया। फिर इन परिणामों का प्रयोग करके, उन्होंने निगमनिक तर्कण (deductive reasoning) द्वारा कुछ और परिणामों को सिद्ध किया। जिन कथनों को सिद्ध किया वे साध्य (propositions) या प्रमेय (theorems) कहलाती थीं।
यहाँ से हम समझ सकते है की प्रमेय या साध्य ऐसे कथन होते है जो पूर्व मे सिद्ध किए जा चुके है।
अब हम एक प्रमेय सिद्ध करेंगे जो विभिन्न परिणामों में अनेक बार प्रयोग की जाती है।
प्रमेय 5.1
दो भिन्न रेखाओं में एक से अधिक बिंदु उभयनिष्ठ नहीं हो सकता।
यहाँ, हमें दो रेखाएँ l और m दी हुई हैं। हमें यह सिद्ध करना है कि l और m में केवल एक बिंदु उभयनिष्ठ है।
इसे हम विरोधाभास मानकर सिद्ध कर सकते हैं अर्थात मान लीजिए कि ये दो रेखाएँ दो भिन्न बिंदुओं P और Q पर प्रतिच्छेद करती हैं।
इस प्रकार, दो भिन्न बिंदुओं P और Q से होकर जाने वाली आपके पास दो रेखाएँ l और m हो जाती हैं परन्तु यह कथन अभिगृहीत 5.1 के विरुद्ध है, जिसके अनुसार दो भिन्न I बिंदुओं से होकर एक अद्वितीय रेखा खींची जा सकती है। अतः, हम जिस कल्पना से चले थे कि दो रेखाएँ दो भिन्न बिंदुओं से होकर जाती हैं गलत है।
इससे निष्कर्ष निकाल सकते हैं कि दो भिन्न रेखाओं में एक से अधिक बिंदु उभयनिष्ठ नहीं होगा।
उदाहरण 1
नीचे दिए पद की परिभाषा दें । क्या इनमें कुछ ऐसे पद हैं । जिन्हे परिभाषित करने की आवश्यकता हैं ? वे क्या हैं और आप इन्हें कैसे परिभाषित कर सकते हैं ?
(i) न्यूनकोण
(ii) आयत
न्यूनकोण - वह कोण जिसका माप समकोण से कम हैं ।
अपरिभाषित पद -
(a) माप
(b) समकोण से कम
(ii) आयत - चार रेखाओं से बना आकृति जिसके चारों कोण बराबर हों आयत कहलाता हैं ।
अपरिभाषित पद :
(a) चार रेखाओं से बना आकृति
(b) कोण
(c) बराबर
उदाहरण 2
सिद्ध कीजिए कि एक दिए हुए रेखाखंड पर एक समबाहु त्रिभुज की रचना की जा सकती हैं ।
माना कि एक दी हुई लम्बाई का एक रेखाखंड AB हैं ।
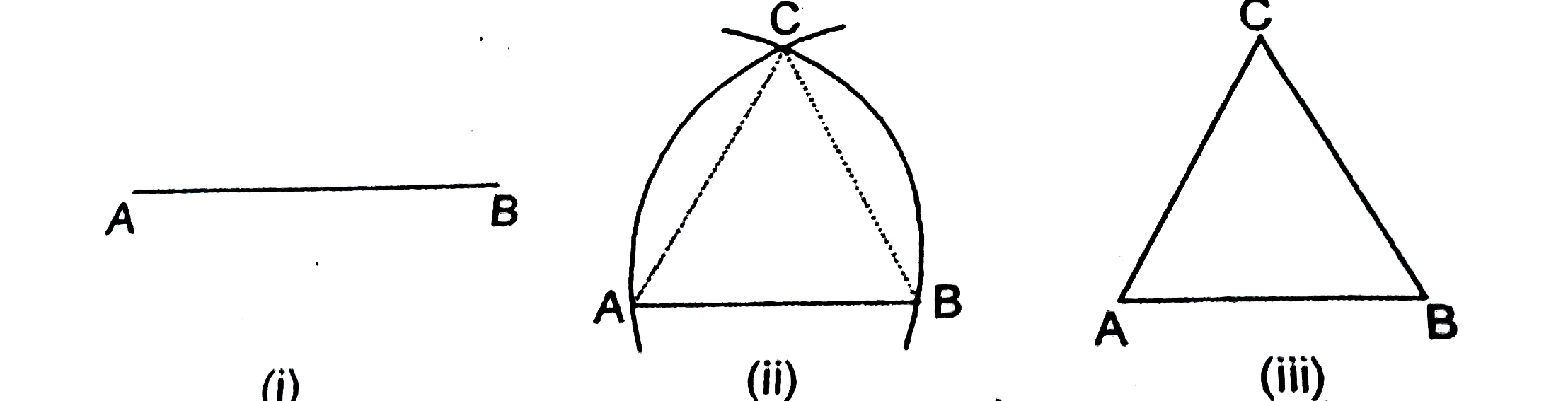
अतः यूक्लिड की अभिधारणा (3) से -
हम बिंदु A को केंद्र और AB त्रिज्या लेकर एक वृत्त खींच सकते हैं । इसी प्रकार , B को केंद्र मानकर और BA त्रिज्या लेकर एक अन्य वृत्त खींचा जा सकता हैं । माना कि ये दोनों वृत्त बिंदु C पर मिलते हैं ।
अब रेखाखंड AC और BC खींचकर △ABC बनाएँ ।
अब हमें यह सिद्ध करना हैं कि यह त्रिभुज एक समबाहु त्रिभुज हैं ,
अर्थात् AB = AC = BC
अब , AB = AC , क्योंकि ये एक वृत्त की त्रिज्याएँ हैं ।......(i)
इसी प्रकार ,
AB = BC , ...(ii)
(i) और (ii) से और यूक्लिड के पहले अभिगृहीत (वे वस्तुएँ जो एक ही वस्तु के बराबर होती हैं एक - दूसरे के बराबर होती हैं ) से
AB = BC = AC
अतः △ABC एक समबाहु त्रिभुज हैं ।
Note : यहाँ यूक्लिड ने , बिना कहीं बताए , यह मान लिया गया हैं कि केंद्रों A और B को लेकर खींचे गए वृत्त परस्पर एक बिंदु पर मिलेंगे ।
उदाहरण 3
यदि AC = BD हैं , तो सिद्ध कीजिए कि AB = CD हैं ।

AC = BD
[दिया हुआ हैं ] ....(i)
AC = AB + BC
[ बिंदु B, बिंदुओं A और C के बीच स्थिति हैं ] ...(ii)
BD = BC + CD
[ बिंदु C , बिंदुओ B और D के बीच स्थिति हैं ] ... (iii)
(ii) और (iii) से (i) में AC तथा BD का मान रखने पर हमें मिलता हैं ,
AB + BC = BC + CD
अतः AB = CD
[ दोनों तरफ से BC घटाने पर , (बराबरों में से बराबरों को घटाने पर ) ]
उदाहरण 4
यदि A, B और C एक रेखा पर स्थित तीन बिंदु हैं और B बिंदुओं A और C के बीच में स्थित है ( देखिए आकृति 5.7 ), तो सिद्ध कीजिए कि AB + BC = AC है |

AB + BC के साथ AC संपाती हैं ।
साथ ही , यूक्लिड का अभिगृहीत (4) के अनुसार वे वस्तुएँ जो परस्पर संपाती हों एक - दूसरे के बराबर होती हैं ।
अतः
AB + BC = AC
Note : यहाँ यह मान लिया गया हैं कि दो बिंदुओं से होकर एक अव्दितीय रेखा खींची जा सकती है ।
OMR (One Minute Revision)
यूक्लिड की पाँचवी अभिधारणा के दो समतुल्य (equal) रूपांतरण:
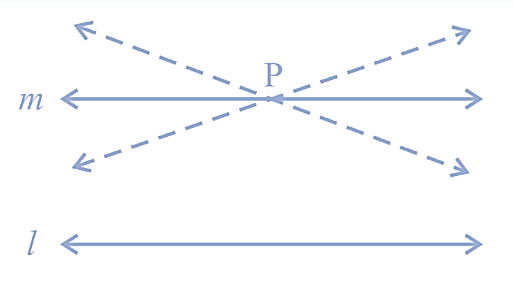
उदाहरण 5
निम्न कथन पर विचार कीजिए :
सीधी रेखाओं के एक ऐसे युग्म का अस्तित्व है, जो एक दूसरे से प्रत्येक स्थान पर समदूरस्थ होती है। क्या यह कथन यूक्लिड की पाँचवी अभिधारणा का एक प्रत्यक्ष (सीधा) परिणाम है ? स्पष्ट कीजिए।
एक रेखा l लीजिए और एक बिंदु ऐसा लीजिए जो रेखा l पर स्थित न हो। तब, प्लेफेयर अभिगृहित से, जो यूक्लिड की पाँचवी अभिधारणा के समतुल्य है, हम जानते है कि P से होकर जाती हुई एक अद्वितीय रेखा m है जो l के समांतर है।
अब, एक बिंदु की एक रेखा से दूरी उस बिंदु से रेखा पर डाले गए लम्ब की लम्बाई होती है। m पर स्थित किसी बिंदु से रेखा l की दूरी और l पर स्थित किसी बिंदु से रेखा m की दूरी सदैव समान होगी। अतः ये दोनों रेखाएँ l और m प्रत्येक स्थान पर एक दूसरे से समदूरस्थ है।
सारांश
अभिगृहीत
वे कल्पनाएँ, जिन्हें निरंतर गणित में प्रयोग किया गया और जिनका केवल ज्यामिति से ही विशेष संबंध नहीं था, अभिगृहीत होती हैं। इन्हे सामान्य अभिधारणाएँ भी कहते हैं
ये निम्नलिखित हैं
अभिधारणा
(ii)दो भिन्न प्रतिच्छेदी रेखाएँ (intersecting lines) कभी भी एक ही रेखा के समांतर नहीं हो सकती।
