रेखाएँ और कोण कक्षा 9 गणित
MOTIVATION
"उठो, जागो और तब तक मत रुको ,
जब तक मंजिल प्राप्त न हो जाये !!
- Swami Vivekananda
हेलो दोस्तों !
स्वागत है आप सभी का Doubtnut के Teacher's Special Notes में।
अब हम शुरू करने जा रहे आपके कक्षा -9 वीं का अध्याय -6 (रेखाएं एवं कोण)
इस अध्याय में हम निम्न बिंदुओं को क्रम से पढ़ेंगे।
भूमिका
दोस्तों यूक्लिड की ज्यामिति से निम्न लिखित महत्वपूर्ण निष्कर्ष निकल कर सामने आये
1 . एक बिंदु से एक अन्य बिंदु तक एक सीधी रेखा खींची जा सकती है।
2 . दिए हुए दो भिन्न बिंदुओं से एक अद्वितीय रेखा खींची जा सकती है।
3.एक शांत रेखा को दोनो छोरों से अनिश्चित रूप से बढ़ाया जा सकता है।
इस अध्याय में हम प्रतिच्छेदी रेखाओं के विषय में जानेगे तथा उनके मध्य बनने वाले कोणों के गुणों का अध्ययन करेंगे
साथ ही हम ऐसे कोणों का भी अध्ययन करेंगे जो दो समांतर रेखाओं को एक तीसरी रेखा द्वारा प्रतिच्छेद करने पर बनते है।
आधारभूत पद और परिभाषाएँ
रेखा-किन्ही दो बिंदुओं को मिलाने वाली अनंत लम्बाई तथा शून्य चौड़ाई वाली ज्यामिति रेखा कहलाती है।
रेखा खंड- रेखा का वह भाग जिसके दो अंत बिंदु हो एक रेखा खंड कहलाता है।
किरण - रेखा का वह भाग जिसका एक अंत बिंदु हो किरण कहलाता है।
संरेख बिंदु -यदि तीन या तीन से अधिक बिंदु एक ही रेखा पर स्थित हो तो वे संरेख बिंदु कहलाते है।
कोण -यदि कोई रेखा अपने एक सिरे को स्थिर रखकर घूमती हुई अपनी स्थिति में परिवर्तन करती है, तो रेखा के परिक्रमण की माप को कोण कहते है।
या जब दो किरणे एक ही अंत बिंदु से प्रारम्भ होते है तो एक कोण बनता है, और दोनों किरणे कोण की भुजाएँ कहलाती है। दोनों किरणों का उभय निष्ठ अंत बिंदु कोण का शीर्ष कहलाता है। कोई भी कोण परिक्रामी रेखा (Revolving Line) द्वारा दो प्रकार से अनुरेखित किया जा सकता है -
(1). यदि परिक्रामी रेखा वामावर्त (Anti Clock Wise) दिशा घूमकर कोण बनाती है तो इस प्रकार से बना कोण धनात्मक (Positive) होता है।
(2). यदि परिक्रामी रेखा दक्षिणावर्त(Clock Wise) दिशा घूमकर कोण बनाती है तो इस प्रकार से बना कोण ऋणात्मक (Nagative) होता है।
(3)धन एवं ऋण कोणों को उनकी राशियों के आगे '+' या '-' का चिह्न लगाकर प्रदर्शित किया जाता है।
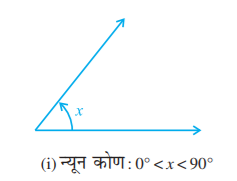
कोणों के प्रकार:(1)-न्यूनकोण:- जिस कोण का मान 0° से बड़ा और 90°से छोटा हो। उसे न्यूनकोण कहते हैं।
2:- समकोण:- जिस कोण का मान 90° होता है। उसे समकोण कहते हैं।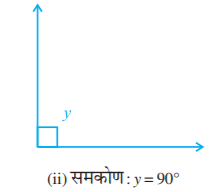
3:- अधिककोण:- जिस कोण का मान 90° से बड़ा और 180° से छोटा हो।उसे अधिककोण कहते हैं।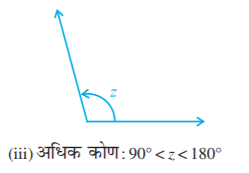
4:ऋजुरेखीय कोण:- जिस कोण का मान 180° हो। उसे ऋजुरेखीय कोण कहते हैं।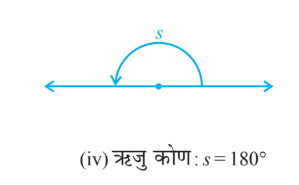
5. वृहत्तकोण या प्रतिवर्ती कोण:- जिस कोण का मान 180° से बड़ा और 360° से छोटा हो। उसे वृहत्तकोण या प्रतिवर्ती कोण कहते हैं।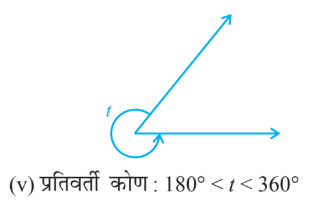
कोणों के युग्म
1.कोटिपुरक कोण या पूरक कोण:-दो कोणों का योगफल 90° हो, तो उन्हें कोटिपुरक कोण कहते हैं।
2.:-सम्पूरक कोण:- दो कोणों का योगफल 180° हो, तो उन्हें सम्पूरक कोण कहते हैं।
3.आसन्न कोण -दो कोण आसन्न कोण कहलाते है यदि उनमे एक उभय निष्ठ शीर्ष हो ,एक उभयनिष्ट भुजा हो तथा जो भुजाएं उभयनिष्ठ न हो वह उभयनिष्ठ भुजा के विपरीत ओर स्थित हो।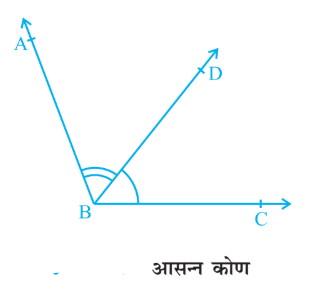
अभिगृहीत- 6.1
यदि एक किरण एक रेखा पर खड़ी हो तो इस प्रकार बने दोनों आसन्न कोणों का योग 180∘होता है।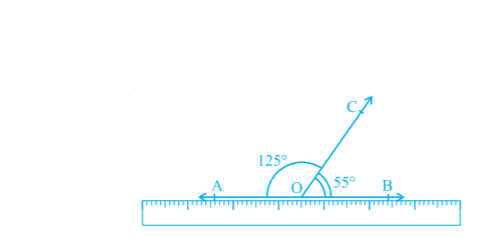
याद कीजिए कि जब दो आसन्न कोणों का योग 180° हो, तो वे कोणों का एक रैखिक युग्म बनाते हैं।
अभिगृहीत 6.1 में यह दिया है कि 'एक किरण एक रेखा पर खड़ी हो'। इस दिए हुए से, हमने निष्कर्ष निकाला कि इस प्रकार बने दोनों आसन्न कोणों का योग 180∘ होता है।
क्या हम अभिगृहीत 6.1 को एक विपरीत प्रकार से लिख सकते हैं?
अर्थात् अभिगृहीत 6.1 के निष्कर्ष को दिया हुआ मानें और उसके दिए हुए को निष्कर्ष मानें। तब हमें यह प्राप्त होगाः
(A) यदि दो आसन्न कोणों का योग 180° है, तो एक किरण एक रेखा पर खड़ी होती है (अर्थात् उभयनिष्ठ भुजाएँ एक ही रेखा में हैं)।
अब आप देखते हैं कि अभिगृहीत 6.1 और कथन (A) एक दूसरे के विपरीत हैं। हम इनमें से प्रत्येक को दूसरे का विलोम (converse) कहते हैं।
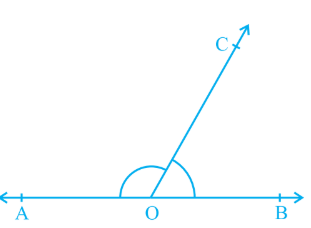
हम यह नहीं जानते कि कथन (A) सत्य है या नहीं। आइए इसकी जाँच करें। विभिन्न मापों के, आकृति 6.7 में दर्शाए अनुसार, आसन्न कोण खींचिए।
प्रत्येक स्थिति में, अउभयनिष्ठ भुजाओं में से एक भुजा के अनुदिश एक पटरी (ruler) रखिए। क्या दूसरी भुजा भी इस पटरी के अनुदिश स्थित है ?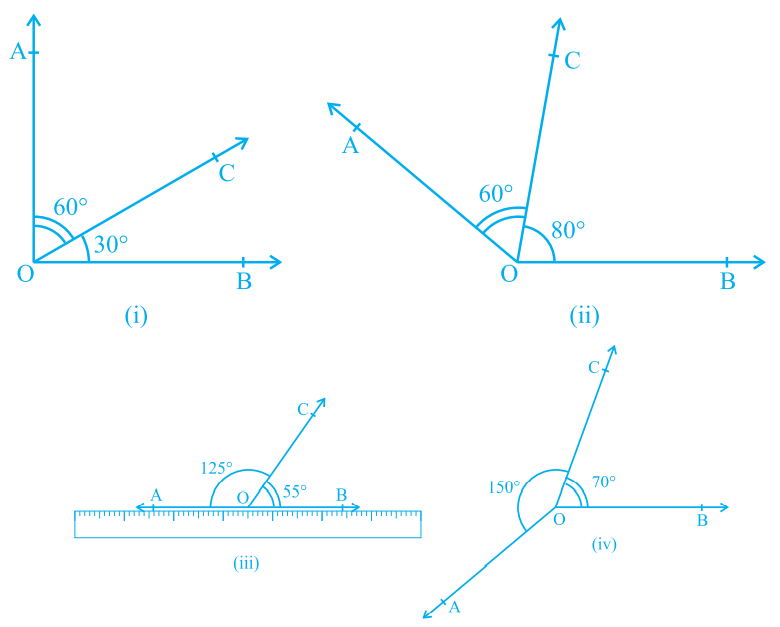
आप पाएंगे कि केवल आकृति 6.7 (iii) में ही दोनों अउभयनिष्ठ भुजाएँ पटरी के अनुदिश हैं, अर्थात् A, O और B एक ही रेखा पर स्थित हैं और किरण OC इस रेखा पर खड़ी है। साथ ही, यह भी देखिए कि ∠AOC+∠COB=125∘+55∘=180∘ है।
अभिगृहीत- 6.2
यदि दो आसन्न कोणों का योग 180∘ है तो उनकी उभयनिष्ठ भुजाएँ एक रेखा बनाती है।
आइए अब उस स्थिति की जाँच करें जब दो रेखाएँ प्रतिच्छेद करती हैं। पिछली कक्षाओं से आपको याद होगा कि यदि दो रेखाएँ परस्पर प्रतिच्छेद करें, तो शीर्षाभिमुख कोण बराबर होते हैं।
OMR (One Minute Revision)
दोस्तों यदि हम इन दोनों अभिग्रहितियों को मिला दे तो हम इसे रैखिक युग्म अभिगृहीत के नाम से भी जानते है।
प्रतिच्छेदी रेखाएँ और अप्रतिच्छेदी रेखाएँ
प्रतिच्छेदी रेखाएँ- दो रेखाएँ जो किसी बिंदु पर प्रतिच्छेद करती है प्रतिच्छेदी रेखाएँ कहलाती है। 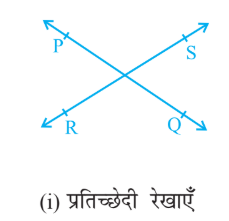
प्रमेय-6.1
यदि दो रेखाएं परस्पर प्रतिच्छेद करती है तो शीर्षाभिमुख कोण बराबर होते है।
दिया है : दो रेखाए परस्पर प्रतिच्छेद करती हैं।
मान लीजिए कि AB और CD दो रेखाएँ हैं जो परस्पर बिंदु O पर प्रतिच्छेद करती हैं,जैसा कि आकृति में दर्शाया गया है।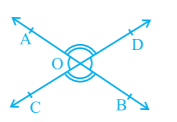
इससे हमें शीर्षांभिमुख कोणों के निम्न दो युग्म प्राप्त होते हैं :
(i)∠AOC और ∠BOD
(ii)∠AOD और ∠BOC हमें सिद्ध करना है कि ∠AOC=∠BOD है और ∠AOD=∠BOC है।
अब किरण OA रेखा CD पर खड़ी है।
अत:,∠AOC+∠AOD=180∘.......(1)
∠AOD+∠BOD=180∘.................(2)
(1)और (2)से,हम लिख सकते हैं किः
∠AOC+∠AOD=∠AOD+∠BOD
इससे निष्कर्ष निकलता है कि ∠AOC=∠BOD
इसी प्रकार,सिद्ध किया जा सकता है कि ∠AOD=∠BOC है।
उदाहरण 1
आकृति में, रेखाएँ AB और CD बिंदु O पर प्रतिच्छेद करती हैं। यदि ∠AOC+∠BOE=70∘ है और ∠BOD=40∘ है, तो ∠BOEऔर प्रतिवर्ती ∠COE ज्ञात कीजिए।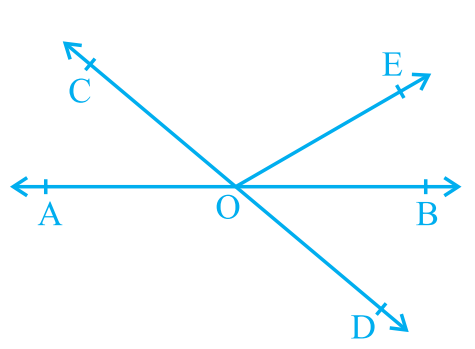
दिया है: रेखाएँ AB और CD बिंदु O पर प्रतिच्छेद करती हैं तथा ∠BOD=40∘ और ∠AOC+∠BOE=70∘
∠AOC=∠BOD [ शीर्षाभिमुख कोण]
अतः, ∠AOC=40∘ [∠BOD=40∘]
इसलिए, समीकरण (1) से,
40∘+∠BOE=70∘
∠BOE=70∘−40∘=30∘
यहाँ, ∠AOC+∠BOE+∠COE=180∘ [ AOB एक रेखा है]
70∘+∠COE=180∘ [समीकरण (1) से]
∠COE=180∘−70∘=110∘
तथा प्रतिवर्ती ∠COE=360∘−∠COE=360∘−110∘=250∘
उदाहरण 2
आकृति में, यदि x+y=w+z है, तो सिद्ध कीजिए कि AOB एक रेखा है।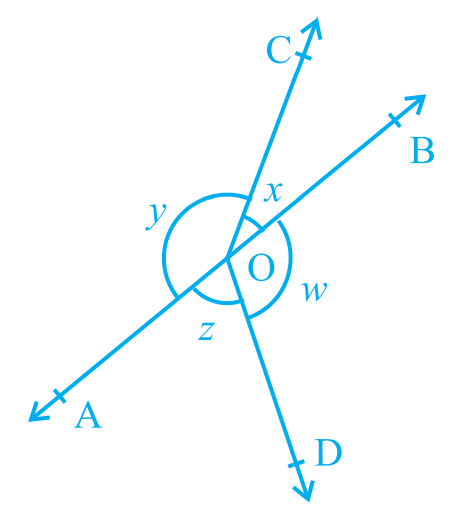
हम जानते हैं कि किसी बिंदु के चरों ओर बने कोणों का योग 360∘ होता है। अतः x+y+w+z=360∘
⇒(x+y)+(w+z)=360∘
⇒(x+y)+(x+y)=360∘ [ दिया है, x+y=w+z]
⇒2(x+y)=360∘
⇒(x+y)=360∘2
x+y=180∘
∠AOC और ∠COB एक रैखिक युग्म बनाते हैं। अतः AOB एक रेखा है।
उदाहरण 3
आकृति में, रेखाएँ XY और MN बिंदु O पर प्रतिच्छेद करती हैं। यदि ∠POY=90∘ और a:b=2:3 है, तो c ज्ञात कीजिए।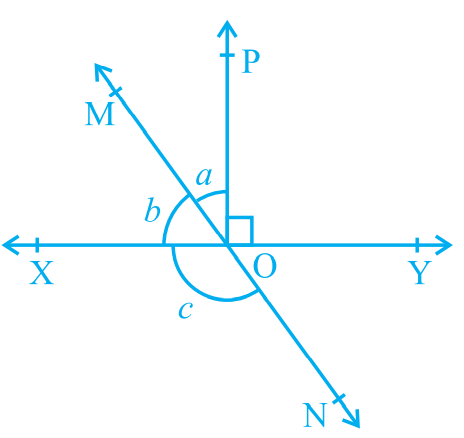
दिया है: रेखाएँ XY और MN बिंदु O पर प्रतिच्छेद करती हैं तथा ∠POY=90∘ और a:b=2:3
माना, a=2x इसलिए b=3x
यहाँ, ∠XOM+∠POM+∠POY=180∘ [XOY एक रेखा है।
3x+2x+90∘=180∘[POY=90∘]
⇒5x+90∘=180∘
5x=180∘−90∘=90∘
x=90∘5=18
अतः, ∠XOM=3x=3×18∘=54∘
और ∠POM=2x=2×18∘=36∘
यहाँ, ∠XON=∠MOY
⇒c=∠POM+∠POY
⇒c=36∘+90∘=126∘ [ शीर्षाभिमुख कोण] [∠XON=c , ∠MOY=∠POM+∠POY]
OMR (One Minute Revision)
यदि दो रेखाएं परस्पर प्रतिच्छेद करती है तो शीर्षाभिमुख कोण बराबर होते है।
समांतर रेखाएँ और तिर्यक रेखा
समान्तर रेखाएँ :दो रेखाएं जो एक दूसरे को कभी प्रतिच्छेद नहीं करती अप्रतिच्छेदी रेखाएँ कहलाती है , इन रेखाओं को हम समांतर रेखाएं भी कहते है क्योंकि इनके बीच की दूरी सदैव एक समान रहती है।
तिर्यक रेखाएँ :वह रेखा जो दो या दो से अधिक रेखाओं को भिन्न-भिन्न बिंदुओं पर प्रतिच्छेद करती है तिर्यक रेखा कहलाती है। 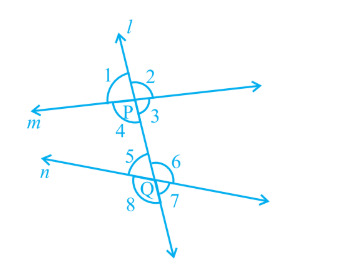
चित्र में रेखा l,रेखाओं m तथा n को दो भिन्न बिंदुओं P तथा Q पर प्रतिच्छेद करती है।इसलिए यहाँ रेखा l तिर्यक रेखा है |
अभिगृहीत- 6.3
यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे , तो संगत कोणों का प्रत्येक युग्म बराबर होता है |
अभिगृहीत 6.3 को संगत कोण अभिगृहीत भी कहा जाता है। आइए अब इस अभिगृहीत के विलोम (converse) की चर्चा करें, जो निम्न है: यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि संगत कोणों का एक युग्म बराबर हो, तो दोनों रेखाएँ समांतर होती हैं। क्या यह कथन सत्य है?
इसकी जाँच निम्न प्रकार की जा सकती है : एक रेखा AD खींचिए और उस पर दो बिंदु B और C अंकित कीजिए। 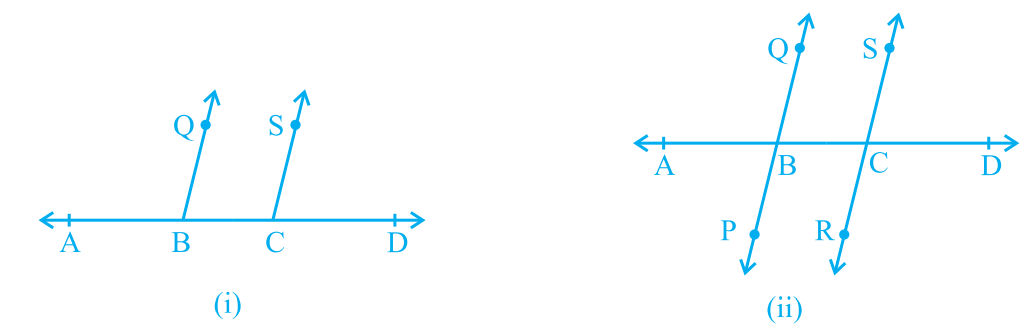
B और C पर क्रमशः ∠ABQ और ∠BCS की रचना कीजिए जो परस्पर बराबर हों, जैसा कि आकृति में दर्शाया गया QB और SC को AD के दूसरी ओर बढ़ाकर रेखाएँ PQ और RS प्राप्त कीजिए, जैसा कि आकृति में दर्शाया गया है।
आप देख सकते हैं कि ये रेखाएँ परस्पर प्रतिच्छेद नहीं करतीं। आप दोनों रेखाओं PO और RS के विभिन्न बिंदओं पर उभयनिष्ठ लम्ब खींच कर और उनकी लम्बाइयाँ माप कर देख सकते हैं कि ये लंबाइयाँ प्रत्येक स्थान पर बराबर हैं।
अतः आप निष्कर्ष निकाल सकते हैं कि ये रेखाएँ समांतर हैं।
अभिगृहीत- 6.4
यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि तिर्यक रेखा के एक ही ओर के संगत कोणों का एक युग्म बराबर हो, तो दोनों रेखायें परस्पर समांतर होती है
क्या हम एक तिर्यक रेखा द्वारा दो समांतर रेखाओं को प्रतिच्छेद करने से बने एकांतर अंतः कोणों के बीच कोई संबंध ज्ञात करने के लिए संगत कोण अभिगृहीत का प्रयोग कर सकते हैं? 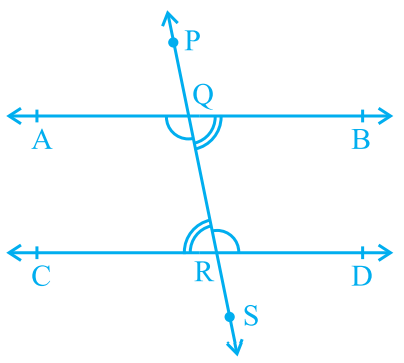
आकृति में, तिर्यक रेखा PS समांतर रेखाओं AB और CD को क्रमशः बिंदुओं Q और R पर प्रतिच्छेद करती है।
क्या ∠BQR=∠QRC और ∠AQR=∠QRD हैं ?
आप जानते हैं कि ∠PQA=∠QRC...... (1) (संगत कोण अभिगृहीत)
क्या ∠PQA=∠BQR है ? ......(2)
हाँ!
इसलिए (1) और (2) से, हम निष्कर्ष निकाल सकते हैं कि ∠BQR=∠QRC
इसी प्रकार,∠AQR=∠QRD
OMR (One Minute Revision)
तिर्यक रेखा द्वारा बनने वाले कोण तथा कोण युग्म 
वाह्य कोण - ∠1,∠2,∠7,∠8 वाह्य कोण कहलाते है।
अन्तः कोण -कोण ∠3,∠4,∠5,∠6 अन्तः कोण है।
संगत कोण -(i)∠1 तथा ∠5
(ii)∠2 तथा ∠6
(iii)∠3 तथा ∠7
(iv)∠4 तथा ∠8
एकान्तर अन्तः कोण- (i)∠4 तथा ∠6
(ii)∠3 तथा ∠5
एकान्तर वाह्य कोण -(i)∠1 तथा ∠7
(ii)∠2 तथा ∠8
तिर्यक रेखा के एक ही ओर के अन्तः कोण (i)∠4 तथा ∠5
(ii)∠3 तथा ∠6
प्रमेय-6.2
यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे तो एकांतर अन्तः कोणों का प्रत्येक युग्म बराबर होता है |
दिया है : दो समांतर रेखाओं l व m है तथा एक तिर्यक रेखा n है |
सिद्ध करना है : ∠3=∠5 तथा ∠4=∠6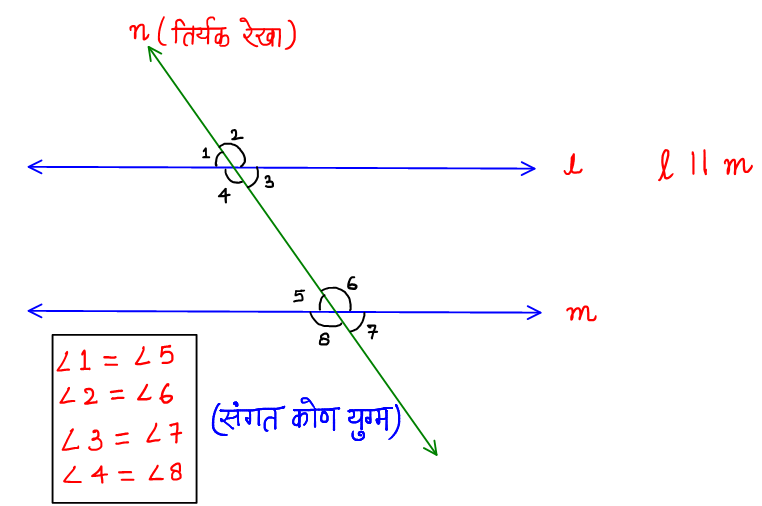
उपपत्ति : ∠3=∠1 (शीर्षाभिमुख कोण)
∠1=∠5
∴∠3=∠5
तथा ∠6=∠8(शीर्षाभिमुख कोण)
∠4=∠8(संगत कोण)
∴∠4=∠6
प्रमेय-6.3
यदि एक तिर्यक रेखा दो समांतर रेखाओं को इस प्रकार प्रतिच्छेद करे कि एकान्तर अन्तः कोणों का युग्म बराबर है, तो दोनों रेखायें परस्पर समांतर होती हैं |
दिया है : दो रेखाएँ P व Q है तथा एक तिर्यक रेखा l इस प्रकार है कि
∠2=∠7
सिद्ध करना है : P∣∣Q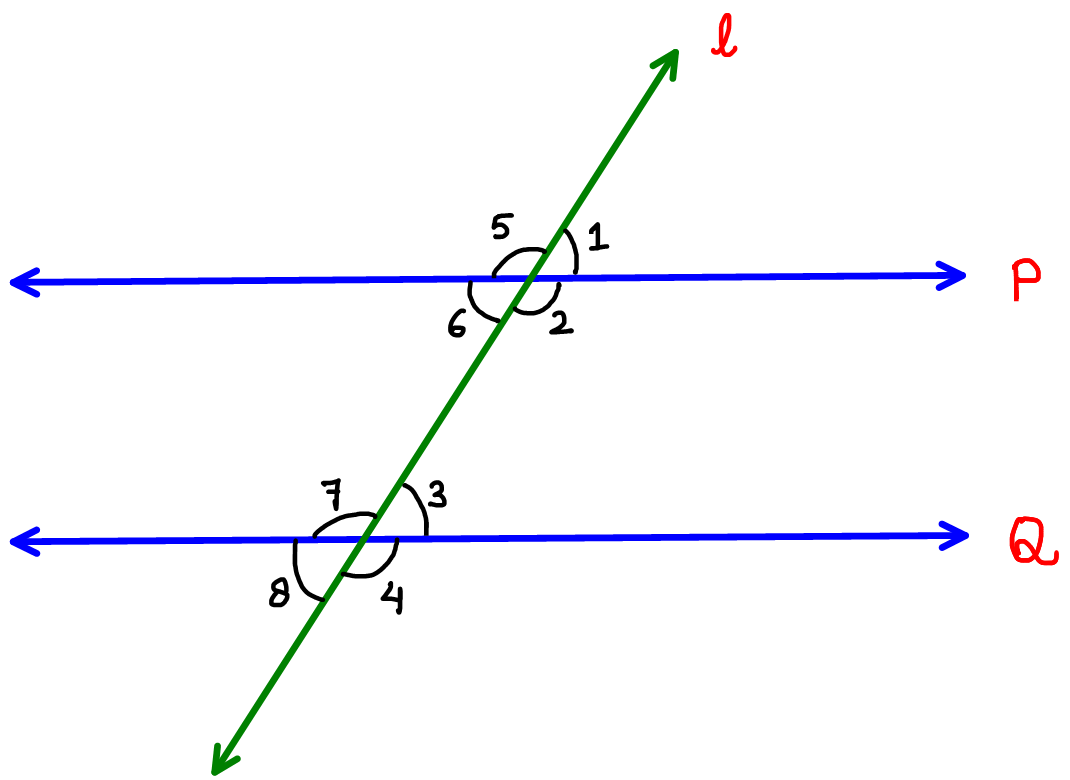
उपपत्ति : ∠2=∠7 (दिया है)
∠7=∠4
∴∠2=∠4(अभिगृहीत 6.4 से )
P∣∣Q
प्रमेय-6.4
यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे तो तिर्यक रेखा के एक ही ओर के अन्तः कोणों का प्रत्येक युग्म सम्पूरक होता है।
दिया है : दो समांतर रेखाओं P व Q है जिन्हे एक तिर्यक रेखा l भिन्न - भिन्न बिंदुओं पर प्रतिच्छेद करती है |
सिद्ध करना है : ∠2+∠3=180∘ तथा ∠6+∠7=180∘
उपपत्ति : ∠1+∠2=180∘ (रैखिक युग्म कोण)
∠1=∠3(संगत कोण)
∴∠2+∠3=180∘
∠5+∠6=180∘ (रैखिक युग्म कोण)
∠5=∠7(संगत कोण)
∴∠6+∠7=180∘
प्रमेय-6.5
यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि तिर्यक रेखा के एक ही ओर के अन्तः कोणों का एक युग्म संपूरक है , तो दोनों रेखायें परस्पर समांतर होती है
दिया है : दो रेखाएँ P व Q है तथा एक तिर्यक रेखा l इस प्रकार है कि ∠2 और ∠7संपूरक कोण है ,
अर्थात ∠2+∠3=180∘
सिद्ध करना है : P∣∣Q
उपपत्ति : ∠2+∠3=180∘ (दिया है)
∠1+∠2=180∘ (रैखिक युग्म कोण)
∴∠2+∠3=∠1+∠2
∠1=∠3
अभिगृहीत 6.4 से ,
P∣∣Q
एक ही रेखा के समांतर रेखाएँ
अब देखिये यदि कोई रेखा किसी दूसरी रेखा के समांतर है तथा दूसरी रेखा किसी अन्य तीसरी रेखा के समांतर है तो पहली रेखा स्वयं तीसरी रेखा के समांतर होगी |
चित्र देखिये -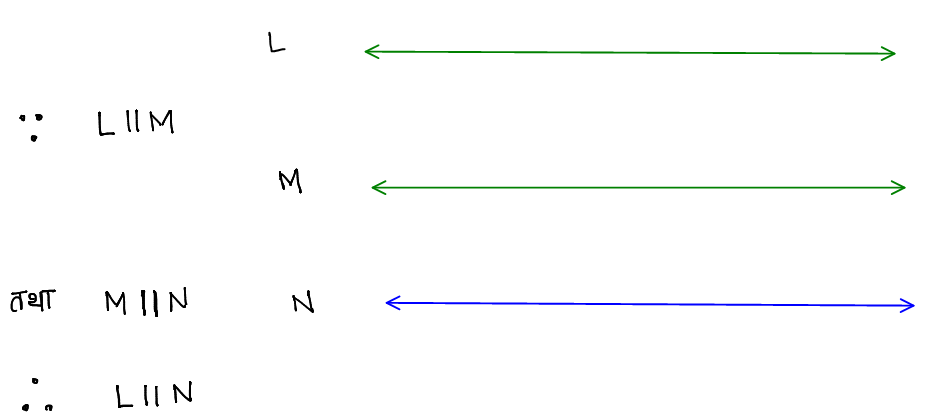
प्रमेय-6.6
वे रेखायें जो एक ही रेखा के समांतर हो परस्पर समांतर होती है |
दिया है : l∣∣m तथा l∣∣n
सिद्ध करना है : m∣∣n
रचना : एक तिर्यक रेखा p खींची |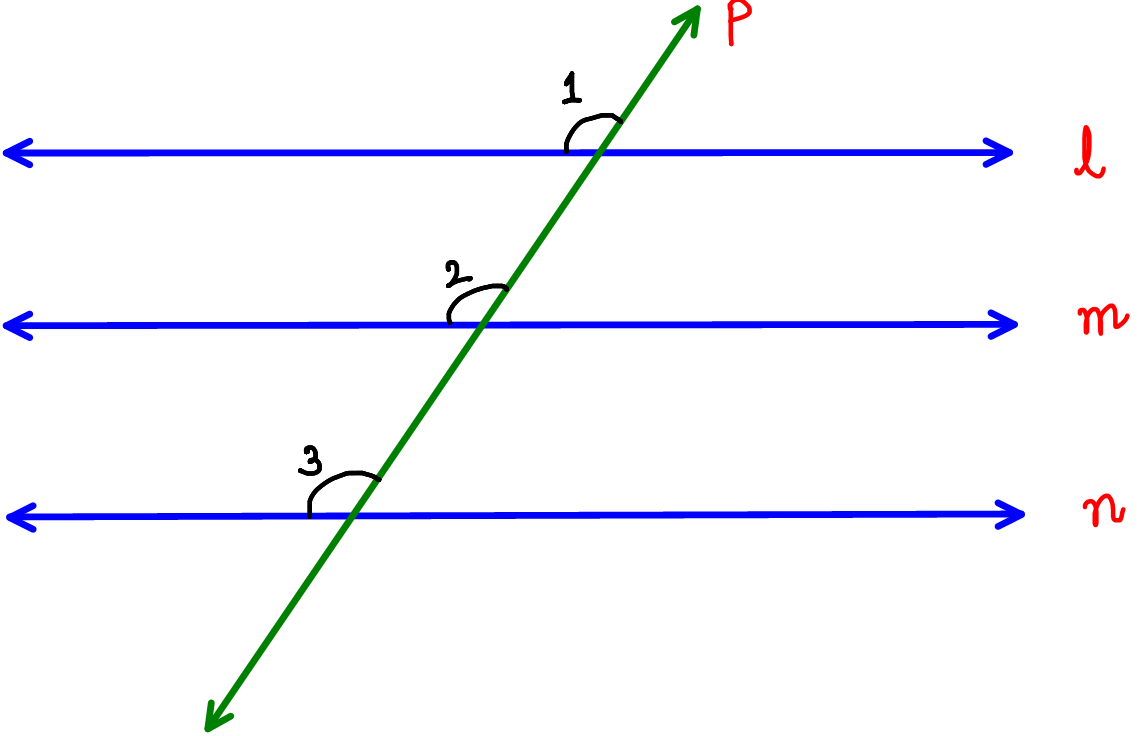
उपपत्ति : l∣∣m
∠2=∠3 (संगत कोण अभिगृहीत )
l∣∣n
∠1=∠2 (संगत कों अभिगृहीत )
:.∠1=∠3
अभिगृहीत 6.4 से ,
m∣∣n
उदाहरण 4
आकृति में यदि PQ∣∣RS,∠MXQ=135∘ और ∠MYR=40∘ है तो XMY ज्ञात कीजिए |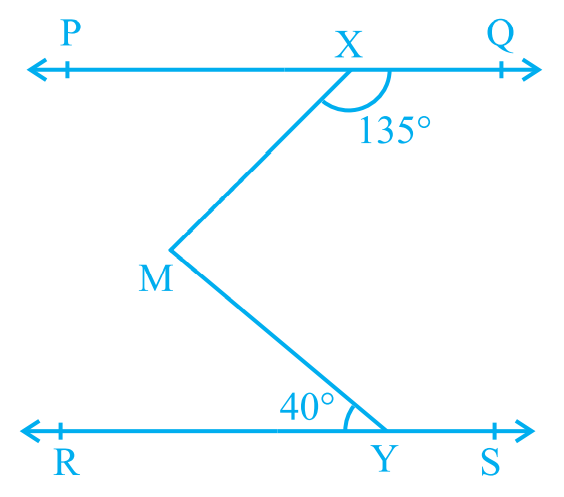
यहाँ हमें m से होकर, रेखा PQ के समांतर एक रेखा AB खींचने की आवश्यकता है, जैसा कि आकृति में दिखाया गया है। अब, AB∣∣PQ और PQ∣∣RS है।
अतः, AB∣∣RS है। (क्यों?)
अब, ∠QXM+∠XMB=180∘
(AB∣∣PQ, तिर्यक रेखा XM के एक ही ओर के अंतः कोण)
∠QXM=135∘ है।
इसलिए, 135∘+∠XMB=180∘
अतः, ∠XMB=45∘........(1)
∠BMY=∠MYR (AB∣∣RS, एकांतर कोण)
∠BMY=40∘ ......(2)
(1) और (2) को जोड़ने पर,
∠XMB+∠BMY=45∘+40∘
अर्थात,∠XMY=85∘
उदाहरण 5
आकृति में, x और y के मान ज्ञात कीजिए और फिर दर्शाइए कि AB || CD है।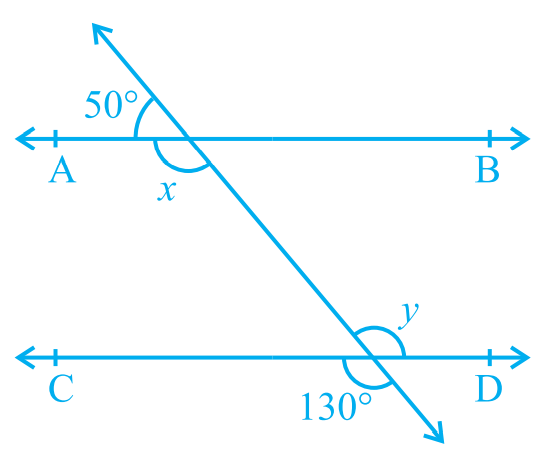
50∘+x=180∘ [ रैखिक युग्म]
x=180∘–50∘=130∘
और y=130∘ [शीर्षाभिमुख कोण]
अतः, x=y=130∘ यहाँ, एकांतर कोणों का एक युग्म बराबर है, अतः AB∣∣CD है।
उदाहरण 6
आकृति में, यदि AB∣∣CD, ∠APQ=50∘ और ∠PRD=127∘ है, तो x और y ज्ञात कीजिए।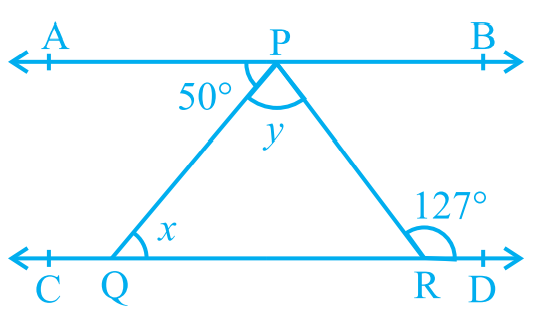
दिया है: PQ∣∣ST,
इसलिए ∠PQR=∠APQ[एकांतर कोण ]
x=50∘
∠APR=∠PRD [एकांतर कोण]
∠APQ+∠QPR=127∘
50∘+y=127∘
y=127∘−50∘=77∘
OMR (One Minute Revision)
वे रेखायें जो एक ही रेखा के समांतर हो परस्पर समांतर होती है |
त्रिभुज का कोण योग गुण
तो बच्चों त्रिभुज का कोण योग गुण उस त्रिभुज के तीनो कोणों से सम्बंधित है इसके अनुसार त्रिभुज के तीनो कोणों का योग 180∘ होता है |
इसका मतलब ये हुआ की त्रिभुज के तीनो कोणों को जोड़ने पर हमे 180∘ मिलता है |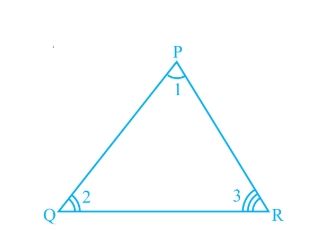
∠1+∠2+∠3=180∘
प्रमेय-6.7
किसी त्रिभुज के कोणों का योग 180∘ है |
दिया है -
एक त्रिभुज ΔPQR है जिसके कोण ∠1,∠2 तथा ∠3 है।
सिद्ध करना है -∠1+∠2+∠3=180∘
रचना -भुजा QR के समांतर उसके सम्मुख शीर्ष P से होकर एक रेखा XPY खींचें,जैसा कि आकृति दर्शाया गया है। 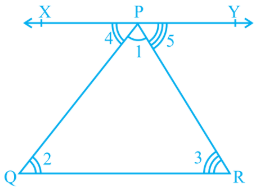
समांतर रेखाओं से सम्बंधित गुणों का प्रयोग करने पर
चूँकि XPY एक रेखा है। अतः ∠4+∠1+∠5=180∘..........(i) है।
परन्तु XPY∣∣QR तथा PQ और PR तियंक रेखाएँ हैं।
इसलिए,∠4=∠2 और ∠5=∠3 (एकांतर कोणों के युग्म)
∠4 और ∠5 के ये मान (i) में रखने पर हमें प्राप्त होता है:
∠2+∠1+∠3=180∘अर्थात ∠1+∠2+∠3=180∘है।
प्रमेय-6.8
यदि एक त्रिभुज की एक भुजा बढ़ाई जाये तो इस प्रकार बना बहिष्कोण दोनों अन्तः अभिमुख (विपरीत) कोणों के योग के बराबर होता है।
दिया है - 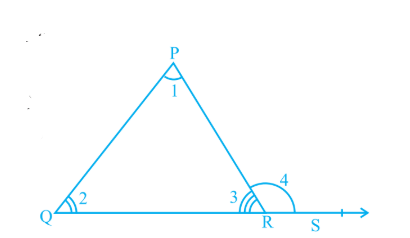
एक त्रिभुज ΔPQRके तीन अन्तः कोण ∠1,∠2 तथा ∠3है।
∠PRS या ∠4 त्रिभुज PQR का एक बहिष्कोण (exterior angle) है।
सिद्ध करना है - ∠4=∠1+∠2
चूँकि ∠3 तथा ∠4 रैखिक कोण युग्म है।
अतः ∠3+∠4=180∘ (1)
चूँकि ∠1,∠2 तथा ∠3 त्रिभुज ΔPQR के तीन अन्तः कोण है
अतः ∠1+∠2+∠3=180∘ (2)
(1) और (2) से,
∠3+∠4=∠1+∠2+∠3
अतः ∠4=∠1+∠2
उदाहरण 7
आकृति में, △PQR की भुजाओं PQ और RQ को क्रमशः बिंदुओं S और T तक बढ़ाया गया है। यदि ∠SPR = 135∘ है और ∠PQT = 110∘ है, तो ∠PRQ ज्ञात कीजिए।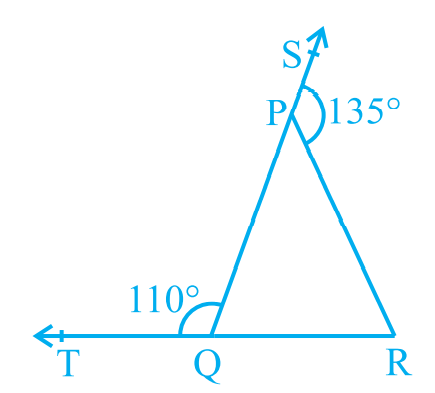
∠PQT + ∠PQR = 180∘[ रैखिक युग्म]
110∘+∠PQR=180∘
∠POR=180∘−110∘=70∘
∠SPR + ∠QPR = 180∘ [रैखिक युग्म]
135∘+ ∠QPR = 180∘
∠QPR = 180∘–135∘=45∘
△PQR में , ∠QPR + ∠PQR + ∠R = 180∘
70∘+45∘+ ∠R = 180∘
115∘+∠R = 180∘
∠R = 180∘−115∘=65∘
उदाहरण 8
आकृति में, यदि AB∣∣DE, ∠BAC=35∘ और ∠CDE=53∘ है, तो ∠DCE ज्ञात कीजिए।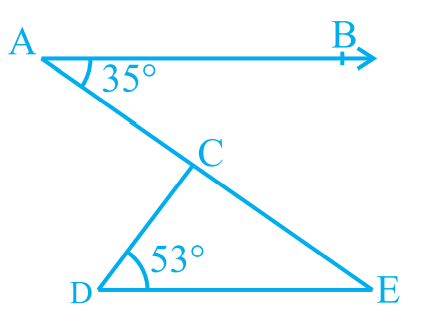
दिया है: AB∣∣DE,
इसलिए ∠CED=∠BAC [एकांतर कोण]
∠CED=35∘
△CDE में,
∠CED+∠CDE+∠DCE=180∘
35∘+53∘+∠DCE=180∘
88∘+∠DCE=180∘
∠DCE=180∘−88∘=92∘
उदाहरण 9
आकृति में, यदि PQ⊥PS,PQ∣∣SR,∠SQR=28∘ और ∠QRT=65∘ है, तो x और y के मान ज्ञात कीजिए।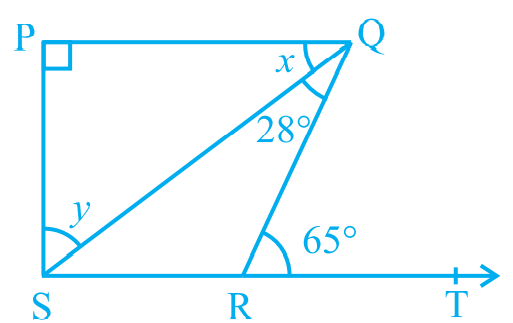
दिया है: PQ⊥PS,
PQ∣∣SR,∠SQR=28∘ और ∠QRT=65∘
∠PQR=∠QR [ एकांतर कोण]
∠RQS+∠PQS=65∘ =
28∘+x=65∘
x=65∘−28∘=37∘
त्रिभुज PQS में,
∠P+∠PQS+∠PSQ=180∘
90∘+37∘+y=180∘
127∘+y=180∘
y=180∘–127∘=53∘
OMR (One Minute Revision)
त्रिभुज के तीनों अन्तः कोणों का योग 180∘ होता है |
सारांश
इस अध्याय में हमने जिन महत्वपूर्ण बिंदुओं पर चर्चा की वह निम्न है :
# दो अन्त्य बिंदु वाला रेखा का भाग रेखाखंड कहलाता है।
# एक अन्त्य बिंदु वाला रेखा का भाग किरण कहलाता है।
# यदि तीन या तीन से अधिक बिंदु एक ही रेखा पर स्थित हो तो वे संरेख बिंदु कहलाते है।
# यदि कोई रेखा अपने एक सिरे को स्थिर रखकर घूमती हुई अपनी स्थिति में परिवर्तन करती है, तो रेखा के परिक्रमण की माप को कोण कहते है।
# दो कोणों का योगफल 90° हो, तो उन्हें कोटिपुरक कोण कहते हैं।
# दो कोणों का योगफल 180° हो, तो उन्हें सम्पूरक कोण कहते हैं।
# दो कोण आसन्न कोण कहलाते है यदि उनमे एक उभय निष्ठ शीर्ष हो ,एक उभयनिष्ट भुजा हो तथा जो भुजाएं उभयनिष्ठ न हो वह उभयनिष्ठ भुजा के विपरीत ओर स्थित हो।
# यदि एक किरण एक रेखा पर खड़ी हो तो इसप्रकार बने दोनों आसन्न कोणों का योग 180∘होता है।
#यदि दो आसन्न कोणों का योग 180∘ है तो उनके अउभयनिष्ठ भुजाएँ एक रेखा बनाती है।
# यदि दो रेखाएं परस्पर प्रतिच्छेद करती है तो शीर्षाभिमुख कोण बराबर होते है।
# वह रेखा जो दो या दो से अधिक रेखाओं को भिन्न भिन्न बिंदुओं पर प्रतिच्छेद करती है तिर्यक रेखा कहलाती है।
# यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे संगत कोणों का प्रत्येक युग्म बराबर होता है।
# यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे की संगत कोणों का एक युग्म बराबर होतो दोनों रेखाएं समांतर होंगी।
#यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करे तो एकान्तर अन्तः कोणों का प्रत्येक युग्म बराबर होता है।
#यदि एक तिर्यक रेखा दो समांतर रेखाओं को प्रतिच्छेद करती है तो क्रमागत अन्तः कोणों का प्रत्येक युग्म सम्पूरक होता है।
# यदि दो समांतर रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करती है तो एकान्तर अन्तः कोणों के किसी भी युग्म की अर्द्धक रेखाएं समांतर होती है।
# यदि एक रेखा दो दी गयी समांतर रेखाओं में से किसी एक पर लम्ब होती है तो वह दूसरी रेखा पर भी लम्ब होती है।
# त्रिभुज के तीनो कोणों का योग 180∘ होता है।
# यदि एक त्रिभुज की एक भुजा बढ़ाई जाये तो इस प्रकार बना बहिष्कोण दोनों अन्तः अभिमुख (विपरीत) कोणों के योग के बराबर होता है।