प्रायिकता कक्षा 9 गणित

Table Of Contents

भूमिका

अध्याय के शीर्षक के अनुसार इस अध्याय मे हम प्रायिकता (Probability) का अध्ययन करेंगे। गणित की वह शाखा, जिसमे घटनाओं के घटित होने या न होने की संभावनाओं का संख्यात्मक अध्ययन किया जाता है, प्रायिकता कहलाता है। पिछली कक्षाओं में हमने प्रायिकता का आभास कुछ प्रयोग जैसे - सिक्के उछालना, पासा फेंकना आदि में कर चुके हैं और उनके परिणाम (outcome) देख चुके हैं। अब इस अध्याय में हम देखेंगे कि एक प्रयोग में एक विशेष परिणाम के घटने का संयोग (chance) किस प्रकार मापा जाता है।

आइये जानते है प्रायिकता (Probability) को और करीब से....

बच्चों! हमे अपने दैनिक जीवन में इस प्रकार के कथन सुनने को मिलते रहते हैं:

1. संभवतः आज वर्षा होगी।
2. मुझे संदेह है कि वह इस परीक्षा में उत्तीर्ण होगा।
3. वार्षिक परीक्षा में कविता के प्रथम आने की संभावना सबसे अधिक है।
4. आज के मैच में भारत के टॉस जीतने का संयोग $50 - 50$ हैं।
5. संभवतः पेट्रोल की कीमत घटेगा।
6. यात्रीगण कृपया ध्यान दें, नौचंदी एक्सप्रेस के यहाँ 12 बजकर 15 मिनट पर प्लेटफार्म संख्या 4 पर आने की संभावना है।

यहाँ ऊपर कथनों में प्रयुक्त संभवतः, संयोग, संदेह, संभावना आदि शब्दों का प्रयोग हुआ है जो किसी बात की अनिश्चित्ता को दर्शाती है।

जैसे:- संभवतः पेट्रोल की कीमत घटेगा का अर्थ है, पेट्रोल की कीमत घट भी सकता है और नहीं भी घट सकता है, पेट्रोल की कीमत घटेगा या नहीं इसकी माप पिछले अनुभवों के अधार पर किया जा सकता है। जब हम यह कहते हैं कि अधिक संभावना है कि आज वर्षा होगी तो इससे यह ज्ञात नहीं होता है कि वर्षा होने की संभावना कितनी है।

प्रायिकता (Probability) के अंतर्गत इस प्रकार के कथनों की निश्चित्ता तथा अनिश्चित्ता की माप का अध्ययन संख्याओं के रूप में किया जाता है।

प्रायिकता : एक पुनरावलोकन (Revision):

संयोग (Chance) : जब एक जैसी कुछ घटना होती है या दो या उससे अधिक घटना या अन्य वस्तु या कहानी का योग होता है, उसे संयोग कहते हैं।

जैसे:- कल दिया हुआ मेरा यह सिक्का संयोग से वापस मेरे ही पास आ गया।

यादृच्छिक परीक्षण (Random Experiment): किसी परीक्षण के यादृच्छिक होने का अर्थ है कि परीक्षण के एक से अधिक संभव परिणाम हैं और निश्चित रूप से यह पूर्वानुमान (prediction) लगाना संभव नहीं है कि वह परिणाम क्या होगा ?

जैसे:- एक सिक्के को उछालने के परीक्षण में, यह पूर्वानुमान तो निश्चित रूप से लगाया जा सकता है कि सिक्का या तो चित (head) होगा या पट (tail) होगा लेकिन यह निश्चित रूप से ज्ञात नहीं है कि चित या पट में से क्या होगा? यदि किसी पासे को एक बार फेंका जाए, तो छः संख्याओं, अर्थात् 1, 2, 3, 4, 5, 6 में से कोई भी एक संख्या प्राप्त हो सकती है, परन्तु यह निश्चित नहीं है कि कौन-सी संख्या प्राप्त होगी।

परिणाम (Outcomes) : किसी घटना के लिए हमारे पास निष्कर्ष के रूप में जितनी भी संभावनायें हैं उसे परिणाम कहा जाता है।

जैसे:- किसी विद्यार्थी की परीक्षा का निष्कर्ष दो में से कोई एक ही होगा या तो पास या फिर फेल। इन्हें हम परीक्षा परिणाम भी कहते हैं।

सम संभावित परिणाम (Equally Likely Outcomes): कुछ प्रयोग ऐसे होते हैं जिनमें प्रत्येक परिणाम के प्राप्त होने की संभावना समान यानि एक जैसी (बराबर) होती है, इस प्रकार के परिणामों को सम संभावित परिणाम कहा जाता हैं।

घटना (Event) : किसी प्रयोग के एक या अधिक परिणामों से एक घटना बनती है।

जैसे:- जब एक पासे को फेंका जाता है तो उस पर कोई सम संख्या प्राप्त करना, एक घटना ही है क्योंकि सम संख्या के लिए हमारे पास संभावित परिणाम 2, 4, 6 हैं।

संयोग को प्रायिकता से जोड़ना (Linking Chances to Probability) : अब हम संयोग और प्रायिकता को एक साथ समझने की कोशिश करते हैं। एक सिक्के को उछालने पर दो परिणाम हो सकते हैं, चित और पट।
ocr_image

लेकिन आपको तो इन दोनों मे से कोई एक ही परिणाम मिलेगा, या तो चित या फिर पट। दोनों एक साथ तो कभी नहीं मिल सकते। अब इसी बात को ऐसे भी कह सकते हैं कि एक सिक्के को उछालने पर चित या पट आने के संयोग (chance) बराबर है। एक चित प्राप्त करने की संभावना 2 परिणामों (चित या पट) में से 1 है अर्थात

\frac{1}{2}

है। दूसरे शब्दों में, हम कहते हैं कि एक चित या एक पट प्राप्त करने की प्रायिकता (Prabability)

\frac{1}{2}

है।

अभिप्रयोग (trial): एक क्रिया है जिससे एक या अधिक परिणाम प्राप्त होते हैं।

जैसे:- पासे को फेंकना अभिप्रयोग हैं और पासे को फेंकने पर 1, 2, 3, 4, 5, 6, जो भी आए ये परिणाम होगा।

Note: अपने अभिप्रयोगों के परिणामों को सीधे देखने पर हम प्रायोगिक (experimental) या आनुभविक (empirical) प्रायिकता प्राप्त करते हैं।

प्रायिकता : एक प्रायोगिक दृष्टिकोण

यहाँ हम देखेंगे कि एक प्रयोग में एक विशेष परिणाम के घटने का संयोग (Chance) किस प्रकार मापा जाता है।

किसी प्रयोग को करने पर कुछ परिणाम प्राप्त होते हैं। प्रयोग के करने पर कुल संभव परिणामों और किसी खास परिणाम के घटने के लिए संभव परिणामों की संख्या के आधार पर उस खास परिणाम के घटने की संभावना (संयोग) का माप किया जाता है।

आनुभविक प्रायिकता (Empirical Probability) : माना की हम लोग एक प्रयोग करते हैं, तथा इसमें कुल अभिप्रयोगों (Trials) की संख्या $n$ है जिसमें से अभिप्रयोगों में घटना $E$ घटित होती है।
अतः किसी घटना (Event) $E$ के घटने की आनुभविक (प्रायोगिक) प्रायिकता (Empirical Probability) निम्न प्रकार से परिभाषित की जाती है:

$P (E) =$
अभिप्रयोगों की संख्या जिनमें घटना घटी है / अभिप्रयोगों की कुल संख्या

अभिप्रयोगों के परिणामों को सीधे देखने पर हम प्रायोगिक (experimental) या आनुभविक (empirical) प्रायिकता प्राप्त करते हैं।

Note:- इस अध्याय में, हम आनुभविक प्रायिकता ज्ञात करेंगे तथा सुविधा के लिए आनुभविक प्रायिकता के स्थान पर केवल प्रायिकता का प्रयोग करेंगे।

जैसे:- एक पासे को

500

बार उछाला एवं उसके ऊपरी सतह पर

2

80

बार आया।
यहाँ कुल अभिप्रयोगों की संख्या

= 500

माना की

E

पासे पर

2

के आने की घटना है।

अत: पासे को फेंकने पर ऊपर

2

के आने की प्रायिकता

P (E) =

अभिप्रयोगों की संख्या जिनमें घटना घटी है अभिप्रयोगों की कुल संख्या

= \frac{80}{500}

= \frac{4}{25} = 0.16

महत्वपूर्ण बिन्दु:-

प्रत्येक घटना की प्रायिकता

0

और

1

के बीच (जिसमें

0

और

1

सम्मिलित हैं) होती है।

0 $\leq$ P(E) $\leq$ 1

सभी प्रायिकताओं का योगफल 1 होता है:

P (E_{1}) + P (E_{2}) + P (E_{3}) +

... ... ... ... ... ...

P (E_{n}) = 1

यदि किसी घटना के घटित होने की प्रायिकता

P (E)

हैं, तो घटना के नहीं घटित होने की प्रायिकता

1 - P (E)

होगा।
जैसे:- यदि किसी घटना के घटित होने की प्रायिकता

\frac{2}{3}

हैं, तो उस घटना के घटना के घटित न होने की प्रायिकता

= 1 - \frac{2}{3} = \frac{1}{3}

होगा।

उदाहरण 1

एक सिक्के को $1000$ बार उछालने पर निम्नलिखित बारंबारताएँ प्राप्त होती है:
चित $= 455$ , पट $= 545$
प्रत्येक घटना की प्रायिकता ज्ञात कीजिए।

यहाँ एक सिक्के को $1000$ बार उछाला गया है, इसलिए अभिप्रयोगों की कुल संख्या $= 1000$

माना की एक चित के आने की घटना E और एक पट के आने की घटना $F$ हैं।

अतः $E$ के घटने की संख्या, अर्थात् चित के आने की संख्या $455$ है।

इसलिए, $E$ की प्रायिकता $=$

चितों के आने की संख्या अभिप्रयोगों की कुल संख्या

\Rightarrow P (E) = \frac{455}{1000} = 0.455

F

के घटने की संख्या, अर्थात् पट के आने की संख्या

545

है।

इसलिए,

F

की प्रायिकता

=

पटों के आने की संख्या अभिप्रयोगों की कुल संख्या

\Rightarrow P (E) = \frac{545}{1000} = 0.545

Note:- यहाँ $P (E) + P (F) = 0.455 + 0.545 = 1$ है, तथा प्रत्येक अभिप्रयोग में $E$ और $F$ ही केवल दो संभव परिणाम हैं।

Learn more

उदाहरण 2

एक पासे को $1000$ बार फेंकने पर प्राप्त परिणामों $1$ , $2$ , $3$ , $4$ , $5$ और $6$ की बारंबारताएँ सारणी में दी गई हैं:

प्रत्येक परिणाम के प्राप्त होने की प्रायिकता ज्ञात कीजिए।

माना की परिणाम 1, 2, 3, 4, 5 तथा 6 प्राप्त करने की घटनाएँ क्रमशः $E_{1}, E_{2}, E_{3}, E_{4}, E_{5}$ तथा $E_{6}$ है।

हम जानते हैं कि, किसी घटना $E$ के घटने की प्रायिकता
$P (E) =$

अभिप्रयोगों की संख्या जिनमें घटना घटी है अभिप्रयोगों की कुल संख्या

यहाँ एक पासे को

1000

बार फेंका गया है, इसलिए अभिप्रयोगों की कुल संख्या (पासा फेंकने की कुल संख्या)

= 1000

परिणाम

1

प्राप्त करने की प्रायिकता

P (E_{1}) =

1

की बारंबारता पासा फेंकने की कुल संख्या

\Rightarrow P (E_{1}) = \frac{179}{1000} = 0.179

इसी प्रकार,

परिणाम

2

प्राप्त करने की प्रायिकता

P (E_{2}) =

2

की बारंबारता पासा फेंकने की कुल संख्या

\Rightarrow P (E_{2}) = \frac{150}{1000} = 0.150

परिणाम

3

प्राप्त करने की प्रायिकता

P (E_{3}) =

3

की बारंबारता पासा फेंकने की कुल संख्या

\Rightarrow P (E_{3}) = \frac{157}{1000} = 0.157

परिणाम

4

प्राप्त करने की प्रायिकता

P (E_{4}) =

4

की बारंबारता पासा फेंकने की कुल संख्या

\Rightarrow P (E_{4}) = \frac{149}{1000} = 0.149

परिणाम

5

प्राप्त करने की प्रायिकता

P (E_{5}) =

5

की बारंबारता पासा फेंकने की कुल संख्या

\Rightarrow P (E_{5}) = \frac{175}{1000} = 0.175

परिणाम

6

प्राप्त करने की प्रायिकता

P (E_{6}) =

6

की बारंबारता पासा फेंकने की कुल संख्या

\Rightarrow P (E_{6}) = \frac{190}{1000} = 0.190

Learn more

OMR (One Minute Revision)

प्रत्येक घटना की प्रायिकता 0 और 1 के बीच (जिसमें 0 और 1 सम्मिलित हैं) होती है।

सभी प्रायिकताओं का योगफल 1 होता है।

जैसे कि ऊपर उदाहरण मे देख सकते हैं कि,

P (E_{1}) + P (E_{2}) + P (E_{3}) + P (E_{4}) + P (E_{5}) + P (E_{6})

= 0.179 + 0.15 + 0.157 + 0.149 + 0.175 + 0.19 = 1

उदाहरण 3

टायर बनाने वाली एक कंपनी तय की गई उन दूरियों का एक रिकार्ड रखती थी, जिसके पहले टायर को बदल देने की आवश्यकता पड़ी। सारणी में 1000 स्थितियों के परिणाम दिखाए गए है:


दूरी (km में)	$4000$ से कम	$4000$ से $9000$ तक	$9001$ से $14000$ तक	$14000$ से अधिक
बारंबारता	$20$	$210$	$325$	$445$

यदि आप इस कंपनी से एक टायर खरीदते है, तो इस बात की प्रायिकता क्या होगी कि
(i) 4000 km की दूरी तय करने से पहले ही इसे बदलना आवश्यक होगा?
(ii) यह 9000 km से भी अधिक दूरी तक चलेगा?
(iii) 4000 km और 14000 km के बीच की कोई दूरी तय करने के बाद इसे बदलना आवश्यक होगा?

दिया हैं;

अभिप्रयोगों की कुल संख्या $= 1000$

(i) उस टायर की बारंबारता, जिसे $4000$ km की दूरी तय करने से पहले बदलना आवश्यक हो $= 20$

माना $4000$ km की दूरी तय करने से पहले टायर बदलना आवश्यक हो, की घटना $E$ हो, तब

$P (E) = \frac{20}{1000} = \frac{1}{50} = 0.02$

(ii) उस टायर की बारंबारता जो $9000$ km से भी अधिक दूरी तक चलेगा $= 325 + 445 = 770$

माना $9000$ km से भी अधिक दूरी तक चलने वाले टायर की घटना $F$ हो, तो

$P (F) =$ $\frac{770}{1000} = 0.77$

(iii) उस टायर की बारंबारता जिसे $4000$ km और $14000$ km के बीच की कोई दूरी तय कर लेने के बाद
बदलना आवश्यक होगा $= 210 + 325 = 535$

माना $4000$ km और $14000$ km के बीच की कोई दूरी तय कर लेने के बाद टायर बदलने की घटना $G$ हो, तो

$P (G) = \frac{535}{1000} = \frac{107}{200} = 0.535$

Learn more

उदाहरण 4

$2$ बच्चों वाले $1500$ परिवारों का यादृच्छया चयन किया गया है और निम्नलिखित आँकड़े लिख लिए गए है :


परिवारों में लड़कियों की संख्या	$2$	$1$	$0$
परिवारों की संख्या	$475$	$814$	$211$

यादृच्छया चुने गए उस परिवार की प्रायिकता ज्ञात कीजिए, जिसमे
(i) दो लड़कियाँ हो
(ii) एक लड़की हो
(iii) कोई लड़की न हो
साथ ही, यह भी जाँच कीजिए कि इन प्रायिकताओं का योगफल 1 है या नहीं।

दिया हैं;
अभिप्रयोगों की कुल संख्या (कुल परिवारों की संख्या) $= 1500$

चूंकि हम जानते हैं कि, किसी घटना $E$ के घटने की प्रायिकता
$P (E) =$

अभिप्रयोगों की संख्या जिनमें घटना घटी है अभिप्रयोगों की कुल संख्या

(i) परिवारों की संख्या जिसमें दो लड़कियाँ हों

= 475

यहाँ, माना की

E_{1} =

चुने गए परिवार में दो लड़कियाँ होने की घटना हैं।

अतः

P (E_{1}) =

दो लड़की वाले परिवारों की संख्या परिवारों की कुल संख्या

\Rightarrow P (E_{1}) = \frac{475}{1500} = \frac{19}{60}

(ii) परिवारों की संख्या जिसमें एक लड़की हों

= 814

यहाँ, माना की

E_{2} =

चुने गए परिवार में एक लड़की होने की घटना हैं।

अतः

P (E_{2}) =

एक लड़की वाले परिवारों की संख्या परिवारों की कुल संख्या

\Rightarrow P (E_{2}) = \frac{814}{1500} = \frac{407}{750}

(iii) परिवारों की संख्या जिसमें कोई लड़की न हो

= 211

माना की

E_{3} =

चुने गए परिवार में कोई लड़की न होने की घटना हैं।

अतः

P (E_{3}) =

कोई लड़की न होने वाले परिवारों की संख्या परिवारों की कुल संख्या

\Rightarrow P (E_{3}) = \frac{211}{1500}

प्रायिकताओं का योगफल

P (E) = P (E_{1}) + P (E_{2}) + P (E_{3})

\Rightarrow P (E) = \frac{19}{60} + \frac{407}{750} + \frac{211}{1500}

\Rightarrow P (E) = 1

अतः प्रायिकताओं का योगफल 1 है।

Learn more

उदाहरण 5

एक कंपनी ने यादृच्छया $2400$ परिवार चुनकर एक घर की आय स्तर और वाहनों की संख्या के बीच संबंध स्थापित करने के लिए उनका सर्वेक्षण किया। एकत्रित किए गए आँकड़े नीचे सारणी में दिए गए हैं: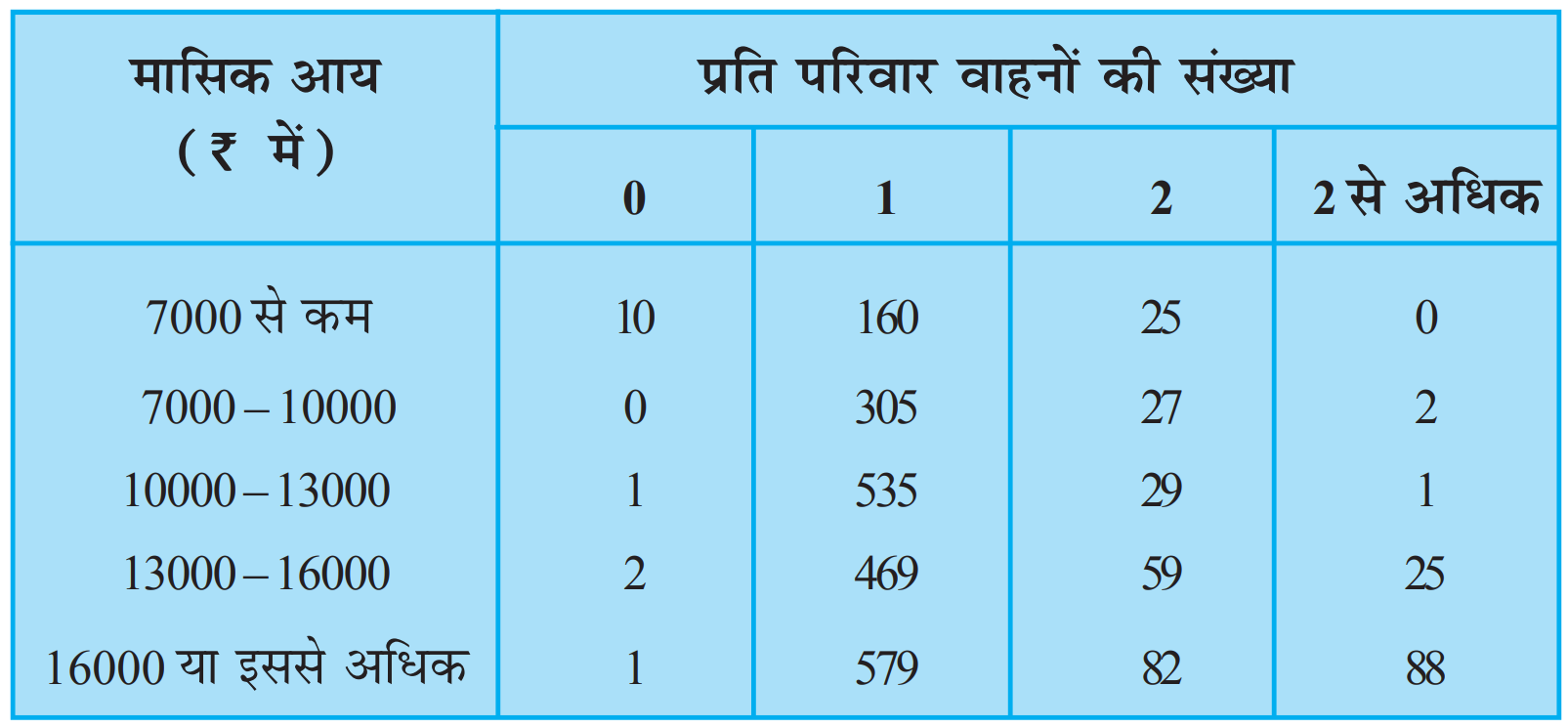

मान लीजिए एक परिवार चुना गया है। प्रायिकता ज्ञात कीजिए कि चुने गए परिवार
(i) की आय ₹10000 - 13000 प्रति माह है और उसके पास ठीक $2$ वाहन हैं।
(ii) की आय प्रति माह ₹16000 या इससे अधिक है और उसके पास ठीक 1 वाहन है।
(iii) की आय प्रति माह ₹7000 से कम है और उसके पास कोई वाहन नहीं है।
(iv) की आय ₹13000 - 16000 प्रति माह है और उसके पास 2 से अधिक वाहन हैं।
(v) जिसके पास 1 से अधिक वाहन नहीं है।

दिया हैं;

कुल परिवारों की संख्या (अभिप्रयोगों की कुल संख्या) $= 2400$

हम जानते हैं कि, किसी घटना $E$ के घटने की प्रायिकता
$P (E) =$

अभिप्रयोगों की संख्या जिनमें घटना घटी है अभिप्रयोगों की कुल संख्या

यहाँ, माना की दी गई घटनाएँ (i), (ii), (iii), (iv) और (v) क्रमशः

E_{1}, E_{2}, E_{3}, E_{4},

और

E_{5}

है।

(i) कुल परिवारों की संख्या

= 2400

ऐसे परिवारों की संख्या

29

हैं जिनकी आय

₹ 10000 - 13000

प्रति माह है और उसके पास ठीक 2 वाहन है।

इसलिए, प्रायिकता

P (E_{1}) = \frac{29}{2400}

(ii) कुल परिवारों की संख्या

= 2400

ऐसे परिवारों की संख्या 579 हैं जिनकी आय प्रति माह

₹ 16000

या इससे अधिक है और उसके पास ठीक 1 वाहन है।

इसलिए, प्रायिकता

P (E_{2}) = \frac{579}{2400} = \frac{193}{800}

(iii) कुल परिवारों की संख्या

= 2400

ऐसे परिवारों की संख्या 10 हैं। जिनकी आय प्रति माह

₹ 7000

से कम है और उसके पास कोई वाहन नहीं है।

इसलिए, प्रायिकता

P (E_{3}) = \frac{10}{2400} = \frac{1}{240}

(iv) कुल परिवारों की संख्या

= 2400

ऐसे परिवारों की संख्या

25

हैं जिनकी आय

₹ 13000 - 16000

प्रति माह है और उसके पास 2 से अधिक वाहन हैं।

इसलिए, प्रायिकता

P (E_{4}) = \frac{25}{2400} = \frac{1}{96}

(v) कुल परिवारों की संख्या

= 2400

ऐसे परिवारों की संख्या जिसके पास

1

से अधिक वाहन नहीं है अर्थात वाहन या तो

1

होंगे या फिर नहीं होंगे।

अतः परिवारों की संख्या जिसके पास

1

से अधिक वाहन नहीं है

=

वाहन न होने वाले परिवारों की संख्या

+

1

वाहन होने वाले परिवारों की संख्या

= (10 + 0 + 1 + 2 + 1) + (160 + 305 + 535 + 469 + 579)

= 14 + 2048

= 2062

इसलिए, प्रायिकता

P (E_{5}) = \frac{2062}{2400} = \frac{1031}{1200}

Learn more

उदाहरण 6

सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए $200$ विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आँकड़ो को नीचे दी गई सारणी में लिख लिया गया है:


मत	विद्यार्थियों की संख्या
पसंद करते हैं	135
पसंद नहीं करते हैं	65

प्रायिकता ज्ञात कीजिए कि यादृच्छया चुना गया विद्यार्थी
(i) सांख्यिकी पसंद करता है (ii) सांख्यिकी पसंद नहीं करता है।

दिया हैं;

(i) कुल विद्यार्थियों की संख्या $= 200$

विद्यार्थियों की संख्या जो सांख्यिकी पसंद करते है $= 135$

माना की $E_{1} =$ यादृच्छया चुने गए विद्यार्थी के सांख्यिकी पसंद करने की घटना

अतः, प्रायिकता $P (E_{1}) =$

अभिप्रयोगों की संख्या जिनमें घटना

E_{1}

घटी है अभिप्रयोगों की कुल संख्या

\Rightarrow P (E_{1}) = \frac{135}{200} = \frac{27}{40}

अतः, सांख्यिकी पसंद करने वाले विद्यार्थियों की प्रायिकता

\frac{27}{40}

हैं।

(ii) कुल विद्यार्थियों की संख्या

= 200

विद्यार्थियों की संख्या जो सांख्यिकी पसंद नहीं करते है

= 65

माना की

E_{2} =

यादृच्छया चुने गए विद्यार्थी के सांख्यिकी पसंद नहीं करने की घटना

अतः, प्रायिकता

P (E_{2}) =

अभिप्रयोगों की संख्या जिनमें घटना

E_{2}

घटी है अभिप्रयोगों की कुल संख्या

\Rightarrow P (E_{2}) = \frac{65}{200} = \frac{13}{40}

अतः, सांख्यिकी पसंद न करने वाले विद्यार्थियों की प्रायिकता

\frac{13}{40}

हैं।

Learn more

उदाहरण 7

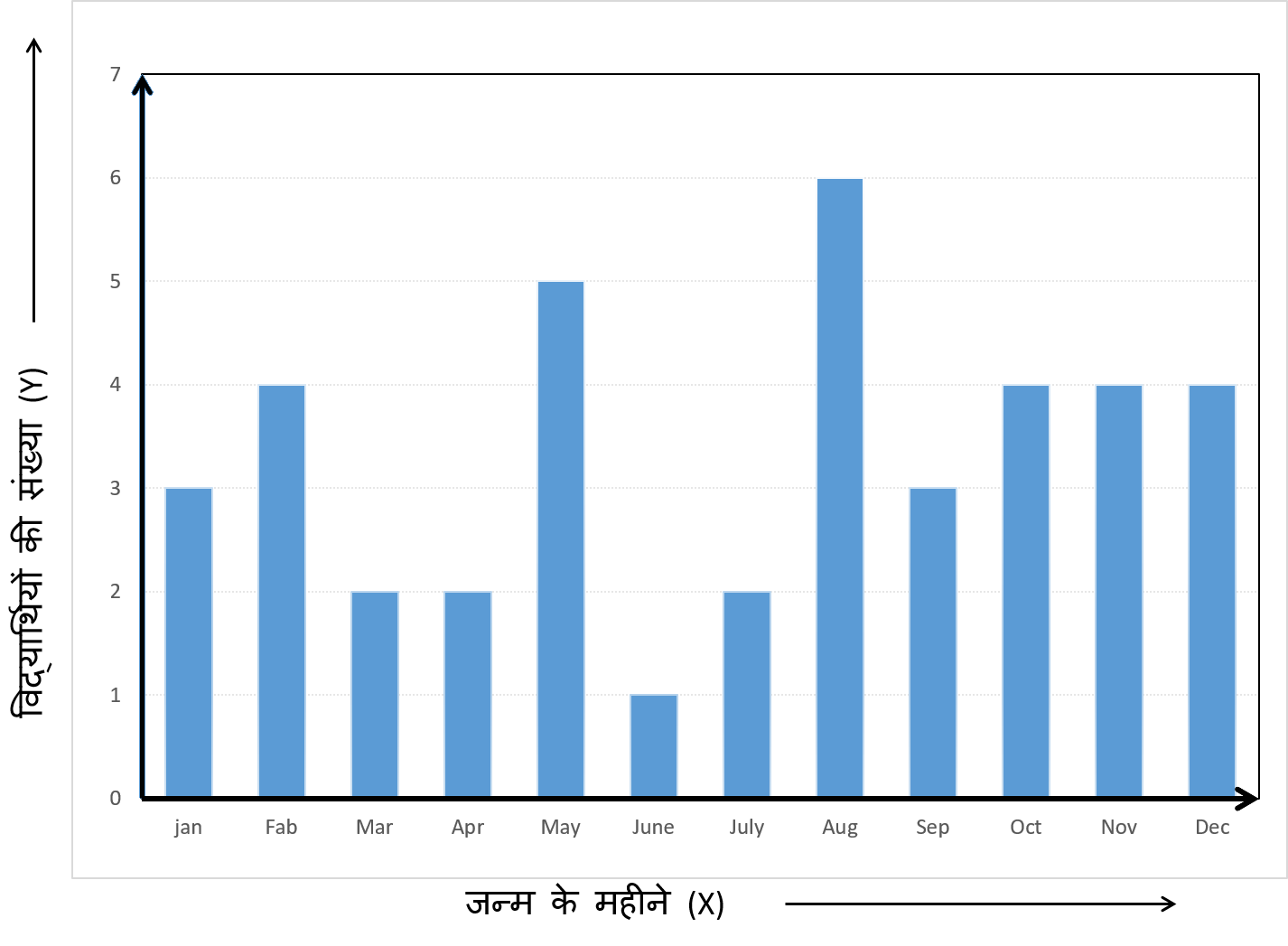
नवीं कक्षा के $40$ विद्यार्थियों से उनके जन्म का महीना बताने के लिए कहा गया। इस प्रकार प्राप्त आंकड़ों से निम्नलिखित आलेख बनाया गया। कक्षा के किसी एक विद्यार्थी का जन्म अगस्त में होने की प्रायिकता ज्ञात कीजिए।

दिया हैं;

कुल विद्यार्थियों की संख्या $= 40$

विद्यार्थियों की संख्या जिनका जन्म अगस्त महीने है $= 6$

माना की $E$ किसी विद्यार्थी का जन्म अगस्त में होने की घटना हैं

अतः प्रायिकता $P (E) =$

अभिप्रयोगों की संख्या जिनमें घटना

E

घटी है अभिप्रयोगों की कुल संख्या

\Rightarrow P (E) = \frac{6}{40} = \frac{3}{20} = 0.15

अतः किसी एक विद्यार्थी का जन्म अगस्त में होने की प्रायिकता

0.15

हैं।

Learn more

उदाहरण 8

एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई $30$ गेंदों में $6$ बार चौका मारती है। चौका न मारे जाने की प्रायिकता ज्ञात कीजिए।

दिया हैं;

महिला बल्लेबाज 30 गेंदें खेलती हैं

अतः, अभिप्रयोगों की कुल संख्या $= 30$

चूंकि 30 गेंदों में 6 बार चौका मारती है।

अतः चौका न मारने की कुल संख्या $= 30 - 6 = 24$

माना की $E =$ चौका न मारे जाने की घटना

अतः, प्रायिकता $P (E) =$

अभिप्रयोगों की संख्या जिनमें घटना

E

घटी है अभिप्रयोगों की कुल संख्या

\Rightarrow P (E) = \frac{24}{30} = \frac{4}{5} = 0.8

अतः चौका न मारे जाने की प्रायिकता

0.8

हैं।

Learn more

उदाहरण 9

इंजीनियर की उनके आवास से कार्य - स्थल की (किलोमीटर में) दूरियाँ ये है :
5, 3, 10, 20, 25, 11, 13, 7, 12, 31,
19, 10, 12, 17, 18, 11, 32, 17, 16,
2, 7, 9, 7, 8, 3, 5, 12, 15, 18, 3, 12,
14, 2, 9, 6, 15, 15, 7, 6, 12
इसकी आनुभविक प्रायिकता (प्रायिकता ) क्या होगी कि इंजीनियर
(i) अपने कार्यस्थल से से 7 km कम दूरी पर रहता है?
(ii) अपने कार्यस्थल से 7 km या इससे अधिक दूरी पर रहता है?
(iii) अपने कार्यस्थल से $\frac{1}{2}$ km या इससे कम दूरी पर रहता है?

यहाँ, कुल इंजीनियरों की संख्या 40 हैं, अतः अभिप्रयोगों की कुल संख्या $= 40$

हम जानते हैं कि, किसी घटना $E$ के घटने की प्रायिकता
$P (E) =$

अभिप्रयोगों की संख्या जिनमें घटना

E

घटी है अभिप्रयोगों की कुल संख्या

(i) कुल इंजीनियरों की संख्या

= 40

माना की

E_{1} =

इंजीनियर के अपने कार्यस्थल से

7

km से कम दूरी पर रहने की घटना

7

km से कम दूरी पर रहने वाले इंजीनियरों की संख्या

= 9

ये दूरियाँ km में 2, 2, 3, 3, 3, 5, 5, 6, 6, है।

इसलिए, प्रायिकता

P (E_{1}) = \frac{9}{40}

अतः अपने कार्यस्थल से

7

km से कम दूरी पर रहने वाले इंजीनियरों की प्रायिकता

\frac{9}{40}

है।

(ii) कुल इंजीनियरों की संख्या

= 40

माना की

E_{2} =

इंजीनियर के अपने कार्यस्थल से

7

km या इससे अधिक दूरी पर रहने की घटना

इंजीनियरों की संख्या जो अपने कार्यस्थल से

7

km या इससे अधिक दूरी पर है

= 31

(ये दूरियाँ

k m

में 7, 7, 7, 7, 8, 9, 9, 10, 10, 11, 11, 12, 12, 12, 12, 12, 13, 14, 15, 15, 15, 16, 17, 17, 18, 18, 19, 20, 25, 31, 32 है।)

इसलिए, प्रायिकता

P (E_{1}) = \frac{31}{40}

अतः, अपने कार्यस्थल से

7

km या इससे अधिक दूरी पर रहने वाले इंजीनियरों की प्रायिकता

\frac{31}{40}

हैं।

(iii) कुल इंजीनियरों की संख्या

= 40

माना की

E_{3} =

इंजीनियर के अपने कार्यस्थल से

\frac{1}{2}

km या इससे कम दूरी पर रहने की घटना
इंजीनियरों की संख्या जो अपने कार्यस्थल से

\frac{1}{2}

km या इससे कम दूरी पर है

= 0

इसलिए, प्रायिकता

P (E_{3}) = \frac{0}{40} = 0

अतः, अपने कार्यस्थल से

\frac{1}{2}

km या इससे कम दूरी पर रहने वाले इंजीनियरों की प्रायिकता

0

है।

Learn more

उदाहरण 10

दो सिक्कों को एक साथ $500$ बार उछालने पर, हमे यह प्राप्त होता है :

दो चित : $105$ बार
एक चित : $275$ बार
कोई भी चित नहीं : $120$ बार

इनमे से प्रत्येक घटना के घटने की प्रायिकता ज्ञात कीजिए।

यहाँ दो सिक्कों को $500$ बार उछाला गया है, इसलिए अभिप्रयोगों की कुल संख्या $= 500$

दो चित के आने की संख्या $= 105$
एक चित आने की संख्या $= 275$
कोई भी चित न आने की संख्या $= 120$

माना की दो सिक्को को उछालने पर दो चित, एक चित, कोई चित नहीं आने की घटना क्रमशः $E_{1}$ , $E_{2}$ एवं $E_{3}$ है।

हम जानते हैं कि, किसी घटना $E$ के घटने की प्रायिकता
$P (E) =$

अभिप्रयोगों की संख्या जिनमें घटना

E

घटी है अभिप्रयोगों की कुल संख्या

अतः, दो चित आने की प्रायिकता

P (E_{1}) =

अभिप्रयोगो की संख्या जिसमे दो चित आता है अभिप्रयोगों की कुल संख्या

\Rightarrow P (E_{1}) = \frac{105}{500} = \frac{21}{100} = 0.21

अब, एक चित आने की प्रायिकता

P (E_{2}) =

अभिप्रयोगो की संख्या जिसमे एक चित आता है अभिप्रयोगों की कुल संख्या

\Rightarrow P (E_{2}) = \frac{275}{500} = \frac{11}{20} = 0.55

अब, कोई चित नहीं आने की प्रायिकता

P (E_{3}) =

अभिप्रयोगो की संख्या जिसमे एक चित आता है अभिप्रयोगों की कुल संख्या

\Rightarrow P (E_{3}) = \frac{120}{500} = \frac{6}{25} = 0.24

अतः दो सिक्के को एक साथ

500

बार उछालने पर,

105

बार दो चित,

275

बार एक चित और

120

बार कोई चित नहीं आने प्रायिकता क्रमशः

0.21

0.55

और

0.24

हैं।

Learn more

सारांश

इस अध्याय में हमने निम्नलिखित बिंदुओं का अध्ययन किया है:

एक प्रयोग की एक घटना प्रयोग के कुछ परिणामों का संग्रह होती है।

अभिप्रयोग (trial) एक क्रिया है जिससे एक या अधिक परिणाम प्राप्त होते हैं।

एक घटना

E

की आनुभविक (या प्रायोगिक) प्रायिकता

P (E)

हैं :

P (E) =

अभिप्रयोगों की संख्या जिनमें

E

घटना घटी है अभिप्रयोगों की कुल संख्या

सभी प्रायिकताओं का योगफल 1 होता है:

P (E_{1}) + P (E_{2}) + P (E_{3}) +

... ... ... ... ... ...

P (E_{n}) = 1

किसी घटना के घटने की प्रायिकता

0

और

1

के बीच (जिसमें

0

और

1

सम्मिलित हैं) होती है।

$0 \leq P (E) \leq 1$

Home
Ask Doubt
Profile