सांख्यिकी कक्षा 9 गणित

भूमिका

अध्याय के शीर्षक के अनुसार इस अध्याय मे हम सांख्यिकी का अध्ययन करेंगे। सांख्यिकी (statistics) का अर्थ वह विषय है जिसमें आंकड़ों के संग्रह, प्रस्तुतीकरण, विश्लेषण का अध्ययन करने के साथ - साथ आंकड़ों से अर्थपूर्ण निष्कर्ष निकालने के बारे में भी अध्ययन किया जाता है। पिछली कक्षाओं में आंकड़ों के प्रबंधन मे, आंकड़ों को एकत्रित करना, उनको सारणी मे रखना तथा उन्हें ग्राफ के रूप में प्रदर्शित करना आदि का अध्ययन किया है। अब हम इस अध्याय मे आंकड़ों का संग्रह, आंकड़ों का प्रस्तुतीकरण (अवर्गीकृत एवं वर्गीकृत बारंबारता बंटन सारणी), आंकड़ों का आलेखीय निरूपण (दंड आलेख, आयतचित्र, बारंबारता बहुभुज) और केन्द्रीय प्रवृत्ति के माप (माध्य, माध्यक, बहुलक) का विस्तार से अध्ययन करेंगे।

आइये जानते है सांख्यिकी को और करीब से....

हमारे दैनिक जीवन में प्रतिदिन हमें तथ्यों, संख्यात्मक अंकों, सारणियों, आलेखों (ग्राफों) आदि के रूप में विभिन्न प्रकार की सूचनाएँ देखने को मिलती रहती हैं।

जैसे:-
1. क्रिकेट में बल्लेबाजी का औसत।
2. क्रिकेट में गेंदबाजी का औसत।
3. परीक्षा में विद्यार्थियों द्वारा प्राप्त किए गए अंक।
4. नगरों के तापमान।
5. मतदान के परिणाम।

ये सूचनाएँ समाचार-पत्रों, विज्ञापनों, पत्र-पत्रिकाओं या अन्य स्रोतों द्वारा हमें प्राप्त होते रहते हैं। इन आंकड़ों का संबंध जीवन के प्रत्येक क्षेत्र से होता है।

जैसे:- खेल-कूद, जनसंख्या वृद्धि, शिक्षा की उन्नति, जन-स्वास्थ्य, कृषि, पंचवर्षीय योजनाओं में व्यय आदि।

सांख्यिकी (STATISTICS)

अर्थपूर्ण सूचनाएँ उपलब्ध करने से संबंधित अध्ययन गणित की एक शाखा में किया जाता है जिसे सांख्यिकी कहते है।

सांख्यिकी के चरण (Stages of statistics) : सांख्यिकी के चार चरण होते हैं:

1. आंकड़ों का संग्रहण (Collection of data): आंकड़ों के अध्ययन के लिए सबसे पहले आंकड़ों को इकट्ठा (collection) करना होता है।

2. प्रस्तुतीकरण (Presentation): आंकड़ों का संग्रहण हो जाने के बाद आंकड़ों को इस प्रकार व्यवस्थित किया जाता है जिससे की इन्हे आसानी से समझा जा सके और इनकी तालिकाएँ (सारणी) या आलेख बनाया जा सके।

3. विश्लेषण (Analysis): आंकड़ों के विश्लेषण का कार्य दी हुई सांख्यिकीय विधियों के अनुसार किया जाता हैं। जब सारे आंकड़ों का प्रस्तुतीकरण हो जाता हैं, तो प्रस्तुतीकरण के आधार पर इनका विश्लेषण किया जाता हैं ताकि अंतिम निष्कर्ष निकाला जा सके।

4.निष्कर्ष (Conclusion): आंकड़ों के अध्ययन में सबसे महत्वपूर्ण कार्य उनके बारे में निष्कर्ष निकालने का होता हैं। अनुभवी तथा प्रशिक्षित साख्यिकों द्वारा यह कार्य किया जाता है ताकि अन्तिम निष्कर्षों को निकालने में कोई त्रुटि न रहे।

जैसे:- अगस्त 2020 में 10 शहरों दिल्ली, मुम्बई, कोलकाता, चेन्नई, जयपुर, रायपुर, श्रीनगर, शिमला, पटना और भोपाल का तापमान क्रमशः

30^{\circ} C

31^{\circ} C

28^{\circ} C

27^{\circ} C

33^{\circ} C

25^{\circ} C

8^{\circ} C

10^{\circ} C

25^{\circ} C

28^{\circ} C

हैं, ये आंकड़ों का संग्रहण हैं।

अब इन आंकड़ों का प्रस्तुतीकरण करेंगे, सारणी या ग्राफ के रूप में जिससे की इन आंकड़ों से अर्थपूर्ण निष्कर्ष निकाल सके।

ocr_image

अतः सारणी से इन आंकड़ों को आसानी से समझा जा सकता हैं की कौन से शहर का तापमान कम या अधिक हैं और निष्कर्ष भी निकाल सकते हैं की कहाँ सबसे अधिक गर्मी या ठंडी हैं।

आंकड़ों का संग्रह

आंकड़े (Data)

एक निश्चित उद्देश्य से एकत्रित किए गए तथ्यों या अंकों को, जो संख्यात्मक या अन्य रूप में हो सकते हैं, आंकड़े (data) कहलाते है।

जैसे :-
1. पिछले

10

टेस्ट मैचों में एक बल्लेबाज द्वारा बनाए गए कुल रन।
2. परीक्षा में विद्यार्थियों द्वारा प्राप्त किए गए अंक।
3. क्रिकेट में गेंदबाजी का औसत।

आंकड़े दो प्रकार के होते हैं -

प्राथमिक आंकड़े (Primary Data)

:

जब कोई अपने दिमाग में एक निश्चित उद्देश्य रखकर सूचनाओं को एकत्रित करता है, तब इस प्रकार एकत्रित किए गए आंकड़ों को प्राथमिक आंकड़े कहा जाता है।

जैसे :-
1. परीक्षा में विद्यार्थियों द्वारा प्राप्त किए गए अंक।
2. कक्षा में छात्रों की संख्या।
3. विद्यालय में पंखों की संख्या।
4. पिछले दो वर्षों के घर की बिजली का बिल।

ये सभी प्राथमिक आंकड़े हैं जिसे हम एकत्रित कर सकते हैं।

गौण आंकड़े (Secondary Data)

:

जहाँ किसी स्रोत से, जिसमें सूचनाएँ पहले से ही एकत्रित हैं, आंकड़े प्राप्त किए गए हों उन आंकड़ों को गौण आंकड़े (secondary data) कहा जाता है अर्थात वे आंकड़ें जो किसी दुसरे के द्वारा पहले ही एकत्रित किये जा चुके है और यदि कोई अन्य विशेषज्ञ इन आंकड़ों का उपयोग करता है तो ये आँकड़ें गौण आंकड़े कहलाते हैं।

जैसे :-
1. क्रिकेट में बल्लेबाजी का औसत।
2. क्रिकेट में गेंदबाजी का औसत।
3. नगरों के तापमान।
4. मतदान के परिणाम।

आंकड़ों के अध्ययन के लिए पहले आंकड़ों को इकट्ठा करना होता है, जिस भी विषय के बारे में हम अध्ययन करना चाहते हैं। इन आंकड़ों में प्राथमिक तथा गौण, दोनों आंकड़ों को शामिल किया जा सकता है फिर एकत्रित किये गए आंकड़ों का अध्ययन करके आंकड़ों को प्रयोग में लाया जाता है।

जैसे :- मान लीजिये आप ये जानना चाहते हैं कि आपकी कक्षा में अगस्त में किस बच्चे ने सबसे ज्यादा छुट्टी ली हैं, तो इसके लिए आपको पहले अगस्त की उपस्थिति के आंकड़ों की ज़रुरत होगी, उसके बिना बता पाना मुश्किल होगा।
ocr_image

अब इसके लिए आपको कक्षा के एक - एक बच्चे से पूछना पड़ेगा कि कौन बच्चा किस दिन आया तथा कौन बच्चे ने किस दिन छुट्टी ली और इस तरह से आंकड़ें इकट्ठे हो जायेंगे, इसे ही आंकड़ों का संग्रह कहते हैं इसका सबसे अच्छा उदाहरण है आपकी कक्षा का उपस्थिति रजिस्टर ( Attendence Register ) जिसमे पूरे महीने की उपस्थिति (Attendence) होती है।

आंकड़ों का प्रस्तुतीकरण

आंकड़ों को एकत्रित करने का काम समाप्त होने के उपरांत ही इन आंकड़ों को ऐसे रूप में प्रस्तुत करने की विधियों को ज्ञात करना होता है जो अर्थपूर्ण हो, सरलता से समझी जा सकती हों और एक ही झलक में उसके मुख्य लक्षणों को जाना जा सके।

अब हम आंकड़ों को प्रस्तुत करने की दो विधियों का अध्ययन करेंगे:
1. सारणी विधि
2. आलेखीय विधि

सारणी विधि : आंकड़ों को सारणी के रूप में प्रदर्शित करने के दो तरीके हैं:
(i) अवर्गीकृत बारंबारता बंटन सारणी या बारंबारता बंटन सारणी
(ii) वर्गीकृत बारंबारता बंटन सारणी

अवर्गीकृत बारंबारता बंटन सारणी या बारंबारता बंटन सारणी

यदि आंकड़े जिस रूप में संकलित किये गये हैं, उसी रूप में रखे जाए, तो ऐसे आंकड़े को अवर्गीकृत आँकड़ा कहा जाता है। अतः यहाँ आंकड़े वर्गीकृत या समूह में नहीं होते हैं, प्रत्येक अलग - अलग होते हैं तथा आंकड़ों की बारंबारता को दर्शाने के लिए एक सारणी बनाते हैं जिसे बारंबारता बंटन सारणी कहते हैं।

उदाहरण से समझते हैं: यदि किसी वर्ग के 20 विद्यार्थियों द्वारा कुल 100 अंकों में प्राप्त अंक निम्नलिखित हों:

ocr_image

इस प्रकार प्राप्त आंकड़ों को यथाप्राप्त आंकड़े (Raw Data) कहा जाता है। हम इन आंकड़ों को बारंबारता बंटन सारणी के रूप में व्यक्त कर सकते हैं।
यहाँ, ऐसे बहुत से विद्यार्थी हैं जिन्होने एक जैसे अंक प्राप्त किए हैं, जैसे की 60 अंक 4 विद्यार्थियों ने प्राप्त किए हैं अतः 60 की बारंबारता 4 होंगी, इसी प्रकार 80 अंक 2 विद्यार्थियों ने प्राप्त किया तो इसकी बारंबारता 2 होंगी आदि।
इन आंकड़ों को और अधिक सरल रूप में समझने के लिए इन्हें हम एक सारणी के रूप में लिखते हैं, जैसा कि नीचे दिया गया है:

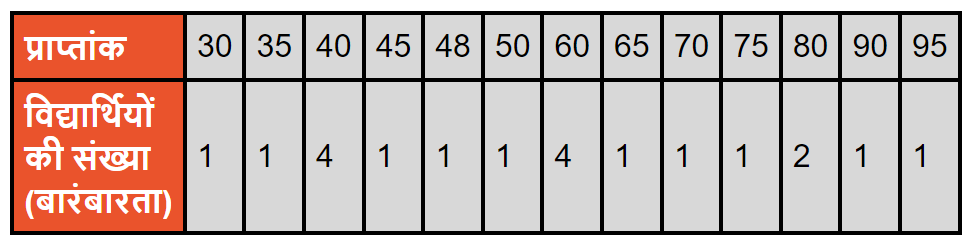
ocr_image

स्पष्ट हैं की, सारणी मे आंकड़ों को उनकी संगत बारंबारताओं के साथ लिखा गया है, जो की इन अवर्गीकृत आंकड़ों का बारंबारता बंटन सारणी हैं। जिससे हम आसानी से अर्थपूर्ण निष्कर्ष निकाल सकते है:

जैसे:-
(i)

60

अंक व

40

अंक प्राप्त करने वाले विद्यार्थियों की संख्या 4 हैं।
(ii)

80

अंक प्राप्त करने वाले विद्यार्थियों की संख्या 2 हैं।

Note: आंकड़ों के संग्रह में कोई पद जितनी बार आता है, वह उस पद की बारंबारता कहलाती है।
उदाहरण:- यदि संग्रह में

4

अंक

7

बार आया है तो

4

की बारंबारता

7

है बारंबारताओं को मिलान चिह्न से भी व्यक्त किया जाता हैं।

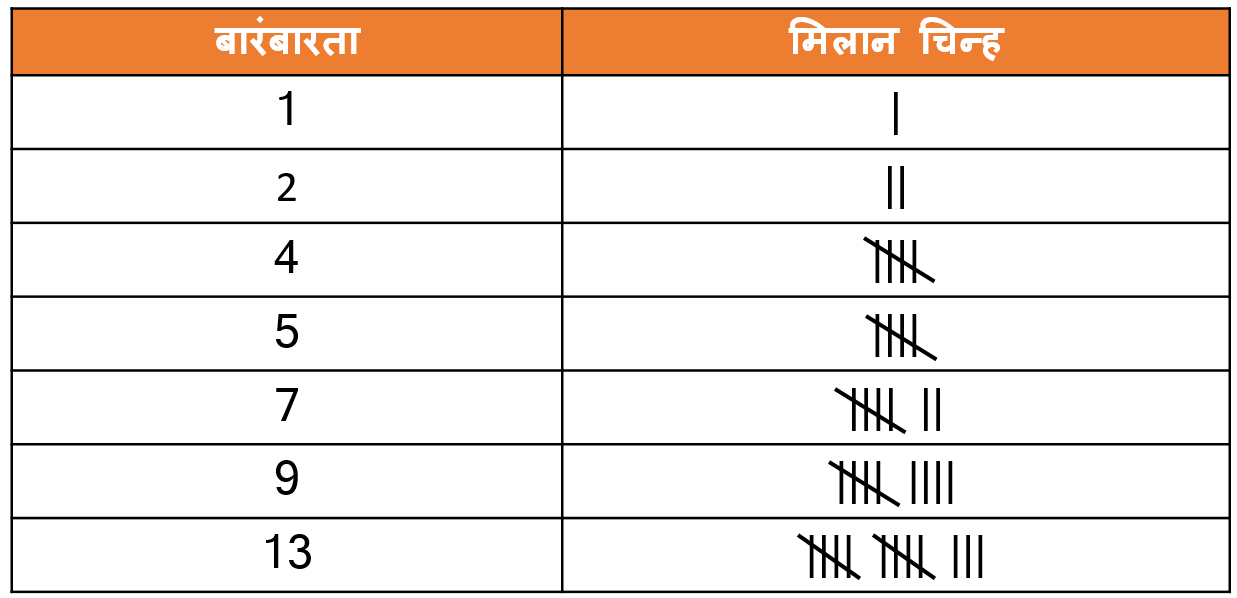
मिलान चिह्न (Tally Marks) : बारंबारताओं की गिनती को सुविधापूर्ण बनाने के लिए एक चिह्न

∣

(दंड) जिसे मिलान चिह्न कहते हैं, का प्रयोग किया जाता है। पाँचवा मिलान चिह्न तिरछा करके पहले वाले दंडों को काटते हुए खींचते हैं।
उदाहरण:-

ocr_image

वर्गीकृत बारंबारता बंटन सारणी

जब आंकड़ों को उनकी विशेषता, लक्षण, समानता के आधार पर विभिन्न वर्गों में बाँट दिया जाता है तो ऐसे आँकड़े वर्गीकृत आंकड़े कहलाते हैं।

जब आंकड़े बहुत बड़ी मात्रा में और अव्यवस्थित रूप में होते हैं, तो साधारण व्यक्ति न तो उन्हे समझ पाता है और न ही उनसे कोई निष्कर्ष निकाल पाता है। संकलित आंकड़ों को संक्षिप्त तथा सरल बनाने के लिए इनका वर्गीकरण किया जाता है। एक प्रकार की विशेषता रखने वाले आंकड़ों को एक वर्ग में रखा जाता हैं, इस प्रकार आंकड़ों को बांटकर जो सारणी बनाते हैं उसको वर्गीकृत बारंबारता बंटन सारणी कहते हैं।

उदाहरण से समझते हैं:
कक्षा VIII के

60

विद्यार्थियों द्वारा गणित में प्राप्त किए गए (

50

में से ) निम्नलिखित अंकों पर विचार कीजिए:

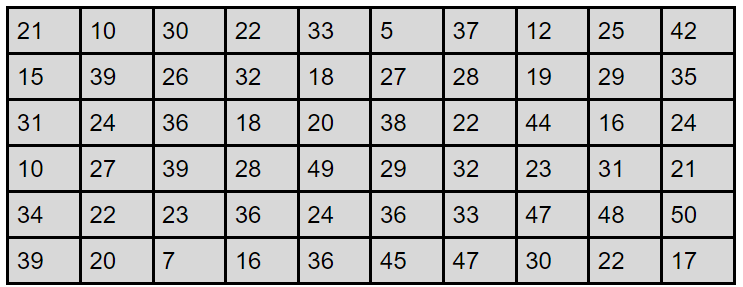
ocr_image

इस स्थिति मे हम यदि प्रत्येक प्रेक्षण के लिए एक बारंबारता बंटन सारणी बनाएंगे, तो वह बहुत लंबी हो जायेंगी। इसलिए हम सुविधा के लिए इन प्रेक्षणों के कुछ समूह या वर्ग बनाते हैं, ( जैसे :- $0 - 10, 10 - 20$ इत्यादि ) फिर प्रत्येक समूह या वर्ग में आने वाले प्रेक्षणों की संख्या के आधार पर एक बारंबारता बंटन (Frequency Distribution) प्राप्त करते हैं।
आइये इन प्रेक्षणों के लिए एक वर्गीकृत बारंबारता बंटन सारणी बनाते है:

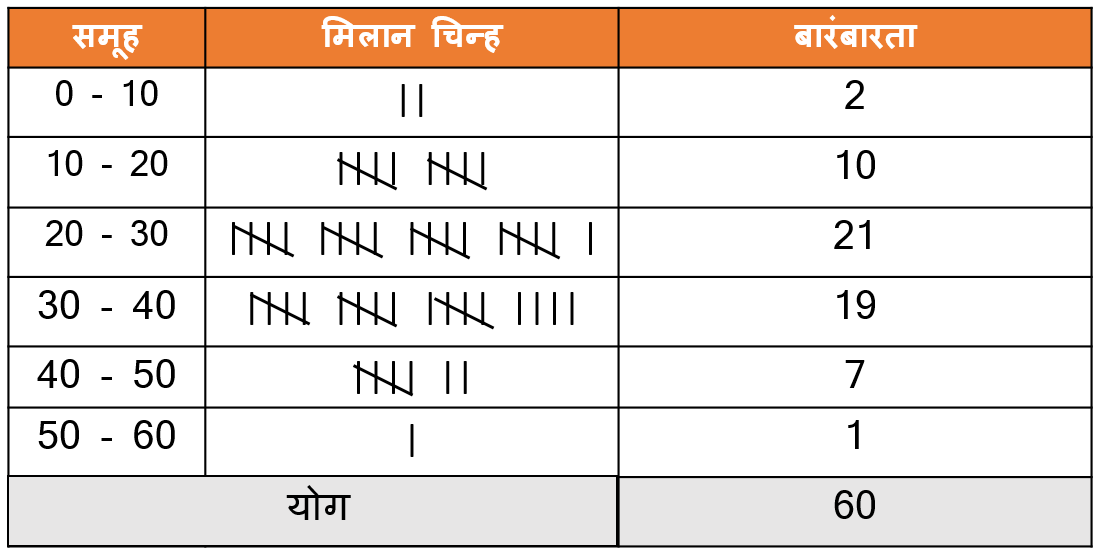
ocr_image

उपर्युक्त प्रकार से व्यवस्थित आंकड़े वर्गीकृत आंकड़े (Grouped Data) कहलाते हैं तथा प्राप्त बंटन वर्गीकृत बारंबारता बंटन कहलाता है। इससे हम आसानी से अर्थपूर्ण निष्कर्ष निकाल सकते है।

कुछ महत्वपूर्ण तथ्य:-

(i) वर्ग - अंतराल या वर्ग : जब सभी अवलोकनों को उनके आकार के अनुसार कई समूहों में वर्गीकृत किया जाता है तो ये समूह वर्ग - अंतराल ( वर्ग ) कहलाते है।
जैसे :-

(0 - 10)

या

(10 - 20)

या

(20 - 30)

इत्यादि ये सभी वर्ग - अंतराल है।

(ii) निम्न - वर्ग सीमा: प्रत्येक वर्ग - अंतराल में कम मान वाली संख्या, निम्न-वर्ग सीमा कहलाती है।
जैसे :- वर्ग अंतराल

(10 - 20)

में

10

निम्न - वर्ग सीमा ( Lower Class Limit ) कहलाती है।

(iii) उच्च - वर्ग सीमा : प्रत्येक वर्ग - अंतराल में अधिक मान वाली संख्या उच्च - वर्ग सीमा कहलाती है।
जैसे :- वर्ग - अंतराल

(10 - 20)

में

20

उच्च - वर्ग सीमा ( Upper Class Limit ) कहलाती है।

(iv) वर्ग - चिह्न (Class marks): वर्ग की उच्च सीमा एवं निम्न सीमा के औसत को वर्ग - चिह्न कहते हैं।

वर्ग - चिह्न

=

उच्च सीमा

+

निम्न सीमा 2

प्रश्न. वर्ग

40 - 60

का वर्ग - चिह्न ज्ञात करें।
यहाँ,
उच्च सीमा

= 60

निम्न सीमा

= 40

वर्ग - चिह्न

= \frac{60 + 40}{2}

= \frac{100}{2} = 50

(v) वर्ग - अंतराल के प्रकार :

(a) अपवर्जी या अतिव्यापी (Exclusive or Overlapping) : इस तरह के वर्ग - अंतराल संतत होते हैं अर्थात यहाँ वर्ग की उच्च (ऊपरी) सीमा तथा अगले वर्ग की निम्न सीमा बराबर होती है।
जैसे:-

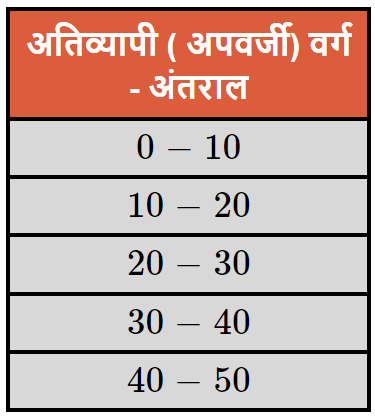
ocr_image

Note :- यहाँ वर्ग की ऊपरी सीमा और अगले वर्ग की निम्न सीमा बराबर होती है अतः वर्ग की ऊपरी सीमा को उस वर्ग में सम्मिलित न कर अगले वर्ग में सम्मिलित किया जाता है।
जैसे :-
वर्ग - अंतराल

(0 - 10)

की ऊपरी सीमा

10

अगले वर्ग - अंतराल

(10 - 20)

की निम्न सीमा हैं तो इस स्थिति मे प्रेक्षण

10

केवल वर्ग - अंतराल

(10 - 20)

में सम्मिलित होगा

(0 - 10)

में नहीं। अतः इसी प्रकार अन्य सभी अंतराल मे करेंगे।

(b) समावेशी या अनतिव्यापी (Inclusive or Non-overlapping) : इस तरह के वर्ग - अंतराल असंतत होते हैं अर्थात यहाँ प्रत्येक वर्ग की उच्च सीमा ठीक अगले वर्ग की निम्न सीमा के बराबर नहीं होती है।
जैसे:-

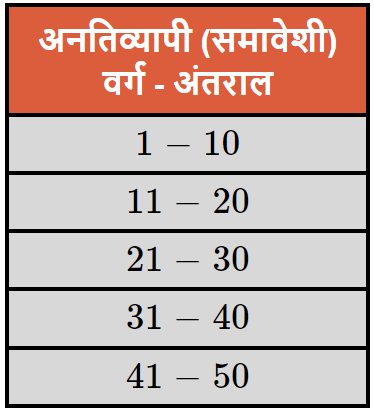
ocr_image

सारणी में लिखा गया वर्ग - अंतराल समावेशी है। यहाँ प्रत्येक वर्ग की उच्च सीमा को उसी वर्ग में शामिल किया गया है।

(vi) रिक्ति (Gap) : समावेशी (अनतिव्यापी) वर्ग - अंतराल में किसी वर्ग की ऊपरी सीमा तथा ठीक बाद वाले वर्ग की निम्न सीमा के अन्तर को रिक्ति कहते हैं।
अतः समावेशी वर्ग अंतराल का रिक्ति

=

किसी वर्ग के ठीक बाद वाले वर्ग की निम्न सीमा

-

उस वर्ग की ऊपरी सीमा।

(vii) वर्ग - अंतराल की चौड़ाई या माप :

(a) जब वर्ग - अंतराल संतत अर्थात अतिव्यापी हो, तो उच्च वर्ग सीमा और निम्न वर्ग सीमा के बीच के अंतर को वर्ग - अंतराल की चौड़ाई या माप (Size) कहते है।
जैसे:-

0 - 10

10 - 20

20 - 30

30 - 40

में

वर्ग - चौड़ाई (माप)

=

उच्च सीमा

-

निम्न सीमा

वर्ग - अंतराल

10 - 20

की वर्ग - चौड़ाई

= 20 - 10 = 10

इसी प्रकार,
वर्ग - अंतराल

20 - 30

की वर्ग - चौड़ाई

= 30 - 20 = 10

वर्ग - अंतराल

30 - 40

की वर्ग - चौड़ाई

= 40 - 30 = 10

(b) जब वर्ग - अंतराल असंतत अर्थात अनतिव्यापी हो, तो वर्ग अंतराल में वर्ग की ऊपरी सीमा तथा निम्न सीमा के अंतर में रिक्ति (gap) को जोड़ने से वर्ग - चौड़ाई (माप) प्राप्त होता है।
जैसे:-

0 - 9

10 - 19

20 - 29

30 - 39

में

वर्ग - चौड़ाई (माप)

=

उच्च सीमा

-

निम्न सीमा

+

रिक्ति

वर्ग - अंतराल

0 - 9

की वर्ग - चौड़ाई

= 9 - 0 + 1 = 10

[(यहाँ रिक्ति 1

(10 - 9 = 1)

हैं]
इसी प्रकार,
वर्ग - अंतराल

10 - 19

की वर्ग - चौड़ाई

= 19 - 10 + 1 = 10

[(यहाँ रिक्ति 1

(20 - 19 = 1)

हैं]
वर्ग - अंतराल

20 - 29

की वर्ग - चौड़ाई

= 29 - 20 + 1 = 10

[(यहाँ रिक्ति 1

(30 - 29 = 1)

हैं]

(viii) अनतिव्यापी (समावेशी) वर्ग - अंतराल को अतिव्यापी (अपवर्जी) वर्ग - अंतराल में बदलना (असंतत वर्ग - अंतराल को संतत वर्ग - अंतराल मे बदलना) :

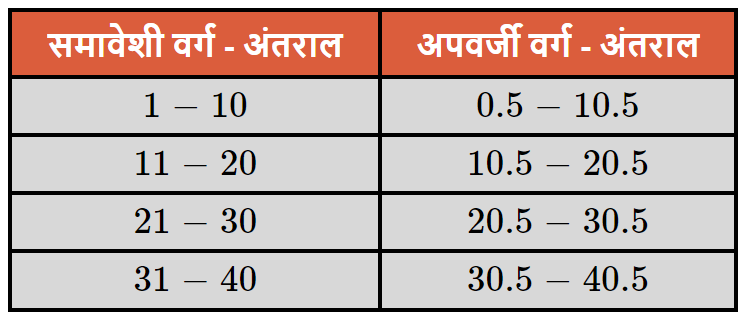
ocr_image

कार्यविधि:- सर्वप्रथम समावेशी (असंतत) वर्ग में रिक्ति (Gap) ज्ञात करना होता हैं।
जैसे:- यहाँ

1 - 10

और

11 - 20

में, 10 और 11 के बीच 1 रिक्ति (Gap) हैं।

अब रिक्ति को आधा करना होता हैं।
जैसे:-

\frac{1}{2} = 0.5

रिक्ति (Gap) के आधे को निम्न सीमा मे घटाना और उच्च सीमा मे जोड़ना होता है।
जैसे :- वर्ग - अंतराल

1 - 10

में,

निम्न सीमा

1 - 0.5 = 0.5

उच्च सीमा

10 + 0.5 = 10.5

इसी प्रकार, वर्ग - अंतराल

11 - 20

में,

निम्न सीमा

11 - 0.5 = 10.5

उच्च सीमा

21 + 0.5 = 21.5

होगा।

अतः इसी तरह सभी असंतत वर्ग - अंतराल को संतत वर्ग - अंतराल मे बदले जाते हैं।

(ix) संचयी बारंबारता (Comulative Frequency) : किसी वर्ग की बारंबारता तथा उस वर्ग के पहले के सभी वर्गों की बारंबारताओं का योग उस वर्ग विशेष की संचयी बारंबारता कहलाती है।
उदाहरण:-

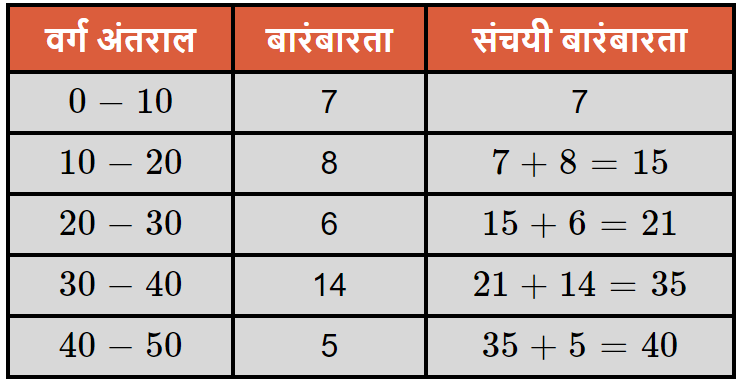
ocr_image

(x) परिसर (Range) : आंकड़ों के अधिकतम और न्यूनतम मानों के अंतर को आंकड़ों का परिसर (range) कहा जाता है।

परिसर

=

अधिकतम मान

-

न्यूनतम मान

जैसे:- एक स्कूल मे 6 बच्चों की आयु 8, 10, 12, 13, 14, 15 वर्ष हैं तो बच्चों की आयु का परिसर क्या होगा ?

स्पष्ट हैं की,
सबसे छोटे बच्चे की आयु

= 8

वर्ष
सबसे बड़े बच्चे की आयु

= 15

वर्ष

अतः बच्चों कि आयु का परिसर

=

सबसे बड़े बच्चे की आयु

-

सबसे छोटे बच्चे की आयु

\Rightarrow 15 - 8 = 7

वर्ष हैं।

OMR (One Minute Revision)

एक निश्चित उद्देश्य से एकत्रित किए गए तथ्यों या अंकों को, जो संख्यात्मक या अन्य रूप में हो सकते हैं, आंकड़े (data) कहलाते है।

जब कोई अपने दिमाग में एक निश्चित उद्देश्य रखकर सूचनाओं को एकत्रित करता है, तब इस प्रकार एकत्रित किए गए आंकड़ों को प्राथमिक आंकड़े कहा जाता है।

जहाँ किसी स्रोत से, जिसमें सूचनाएँ पहले से ही एकत्रित हैं, आंकड़े प्राप्त किए गए हों उन आंकड़ों को गौण आंकड़े (secondary data) कहा जाता है।

किसी प्रेक्षण में कोई चर मान जितनी बार आता है वही उस चर मान की बारंबारता कहलाता है। बारंबारता को मिलान चिह्न से भी दर्शाया जाता हैं।

यदि आंकड़े जिस रूप में संकलित किये गये हैं, उसी रूप में रखे जाए, तो ऐसे आँकड़े को अवर्गीकृत आँकड़ा कहा जाता है।
जैसे:- 10, 5, 7, 9 , 15, 14, 9, 5, 25, 67, 20, 10, 9

जब आंकड़ों को उनकी विशेषता, लक्षण, समानता के आधार पर विभिन्न वर्गों में बाँट दिया जाता है तो ऐसे आंकड़े वर्गीकृत आंकड़े कहलाते हैं।
जैसे:-

0 - 10

10 - 20

20 - 30

30 - 40

या

0 - 9

10 - 19

20 - 29

30 - 39

जब सभी अवलोकनों को उनके आकार के अनुसार कई समूहों में वर्गीकृत किया जाता है तो ये समूह वर्ग - अंतराल ( वर्ग ) कहलाते है।

प्रत्येक वर्ग अंतराल में कम मान वाली संख्या, निम्न - वर्ग सीमा कहलाती है।

प्रत्येक वर्ग अंतराल में अधिक मान वाली संख्या उच्च - वर्ग सीमा कहलाती है।

वर्ग की उच्च सीमा एवं निम्न सीमा के औसत को वर्ग - चिह्न कहते हैं।

वर्ग - चिह्न

=

उच्च सीमा

+

निम्न सीमा 2

आंकड़ों की बारंबारता को दर्शाने के लिए एक सारणी बनाते हैं जिसे अवर्गीकृत बारंबारता बंटन सारणी या बारंबारता बंटन सारणी कहते हैं।

जब आंकड़े बहुत बड़ी मात्रा में और अव्यवस्थित रूप में होते हैं, तो एक प्रकार की विशेषता रखने वाले आंकड़ों को एक वर्ग में रखा जाता हैं, इस प्रकार आंकड़ों को बांटकर जो सारणी बनाते हैं उसको वर्गीकृत बारंबारता बंटन सारणी कहते हैं।

उदाहरण 1

आठवीं कक्षा के 29 विद्यार्थियों के रक्त समूह ये है: $A$ , $B$ , $O$ , $O$ , $A B$ , $O$ , $A$ , $B$ , $A$ , $O$ , $B$ , $A$ , $O$ , $O$ , $A$ , $A B$ , $O$ , $A$ , $A$ , $O$ , $O$ , $A B$ , $B$ , $A$ , $O$ , $B$ , $A$ , $B$ , $O$
इन आंकड़ों को एक बारंबारता बंटन सारणी के रूप में प्रयुक्त कीजिये। बताइये की इन विद्यार्थियों में कौन - सा रक्त समूह अधिक सामान्य है और कौन - सा रक्त समूह विरलतम रक्त समूह है।

दिए गए आंकड़ों के अनुसार 9 विद्यार्थियों का रक्त समूह $A$ है, 6 विद्यार्थियों का रक्त समूह $B$ है, 3 विद्यार्थियों का रक्त समूह $A B$ है तथा 11 विद्यार्थियों का रक्त समूह $O$ है।

29 विद्यार्थियों के रक्त समूह की बारंबारता बंटन सरणी:

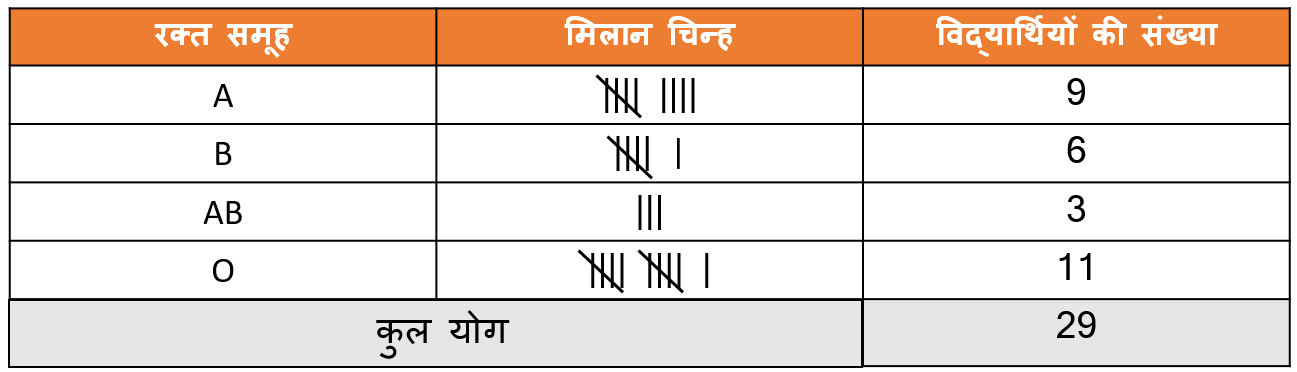
चूंकि रक्त समूह

O

की बारंबारता अधिक 11 है इसलिए रक्त समूह

O

अधिक सामान्य है तथा रक्त समूह AB की बारंबारता सबसे कम है इसलिए रक्त समूह

A B

विरलतम रक्त समूह हैं।

Learn more

उदाहरण 2

किसी परीक्षा में आठवीं कक्षा के छात्रों ने गणित में निम्नलिखित अंक प्राप्त किये:

42, 21, 51, 37, 42, 42, 37, 38, 52, 49, 71, 17,
33, 39, 53, 14, 51, 44, 07, 52, 37, 21, 33, 39,
37, 42, 33, 21, 38, 37, 17, 34, 42, 52, 21, 51

इन आंकड़ों से एक बारंबारता बंटन सारणी बनाये और निम्नलिखित प्रश्नों के उतर दे:
(i) सबसे अधिक अंक पाने वालो की संख्या कितनी है?
(ii) सबसे कम अंक पाने वालो की संख्या कितनी है?
(iii) यदि उत्तीर्णांक 30 अंक हो तो कितने छात्र अनुत्तीर्ण हुए?
(iv) प्राप्तांको का परिसर क्या है ?

दिए गए आंकड़ों की बारंबारता बंटन सारणी:

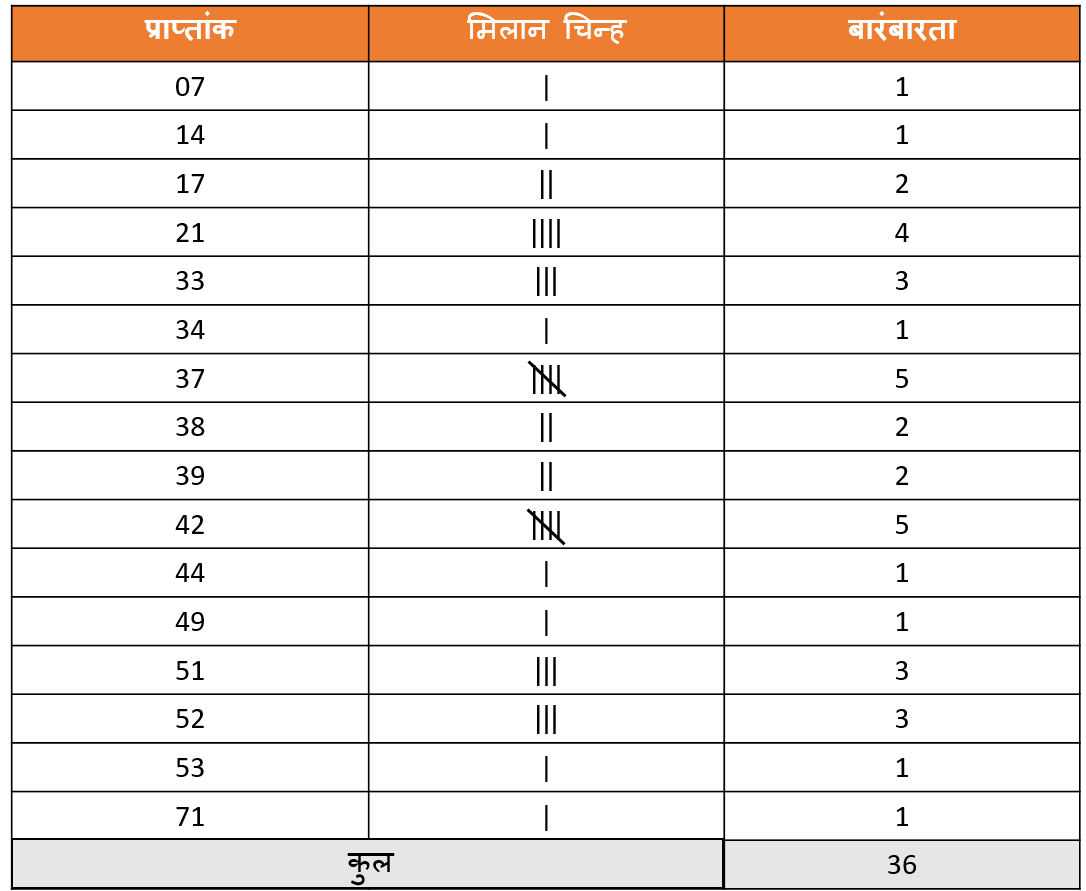
सारणी से स्पष्ट है की,

(i) दिए गए आंकड़ों में

71

सबसे बडा हैं और इसकी बारंबारता

1

हैं अतः सर्वाधिक अंक

(71)

पाने वालो की संख्या

1

है।

(ii) दिए गए आंकड़ों में

07

सबसे छोटा हैं और इसकी बारंबारता

1

हैं अतः सबसे कम अंक

(07)

पाने वालो की संख्या

1

है।

(iii) चूंकि उत्तीर्ण अंक 30 हैं। अतः अनुत्तीर्ण हुए छात्रों के अंक 30 से कम होंगे।

यहाँ,

7

अंक

1

छात्र ने,

14

अंक

1

छात्र ने,

17

अंक

2

छात्रों ने तथा

21

अंक

4

छात्रों ने प्राप्त किया हैं।
अतः

30

से कम अंक प्राप्त करने वाले छात्रों की संख्या

= 1 + 1 + 2 + 4 = 8

अतः अनुत्तीर्ण हुए छात्रों की संख्या

8

हैं।

(iv) हम जानते हैं की,
प्राप्तांको का परिसर

=

उच्चतम अंक

-

निम्नतम अंक

= 71 - 07 = 64

अतः प्राप्तांको का परिसर

64

होगा।

Learn more

उदाहरण 3

30 दिन वाले महीने में एक नगर की सापेक्ष आर्द्रता ( % में ) यह रही है :

98.1, 98.6, 99.2, 90.3, 86.5, 95.3, 92.9, 96.3,
94.2, 95.1, 89.2, 92.3, 97.1, 93.5, 92.7, 95.1,
97.2, 93.3, 95.2, 97.3, 96.2, 92.1, 84.9, 90.2,
95.7, 98.3, 97.3, 96.1, 92.1, 89

(i) वर्ग $84 - 86$ , $86 - 88$ आदि लेकर एक वर्गीकृत बारंबारता बंटन बनाइये।
(ii) क्या आप बता सकते है कि ये आंकड़े किस महीने या ऋतू से संबंधित है ?
(iii) इन आंकड़ों का परिसर क्या है?

(i) दिए गए आंकड़ों में न्यूनतम और अधिकतम सापेक्षित आर्द्रता (% में) क्रमश: $84.9$ और $99.2$ हैं। यह दिया है कि वर्ग $84 - 86$ , $86 - 88$ लेना है, इसलिए वर्गों का माप समान है। अतः समान आकार के बंटन $84 - 86$ , $86 - 88$ , $88 - 90$ ,..., $98 - 100$ होंगे।

वर्गीकृत बारंबारता बंटन सारणी:

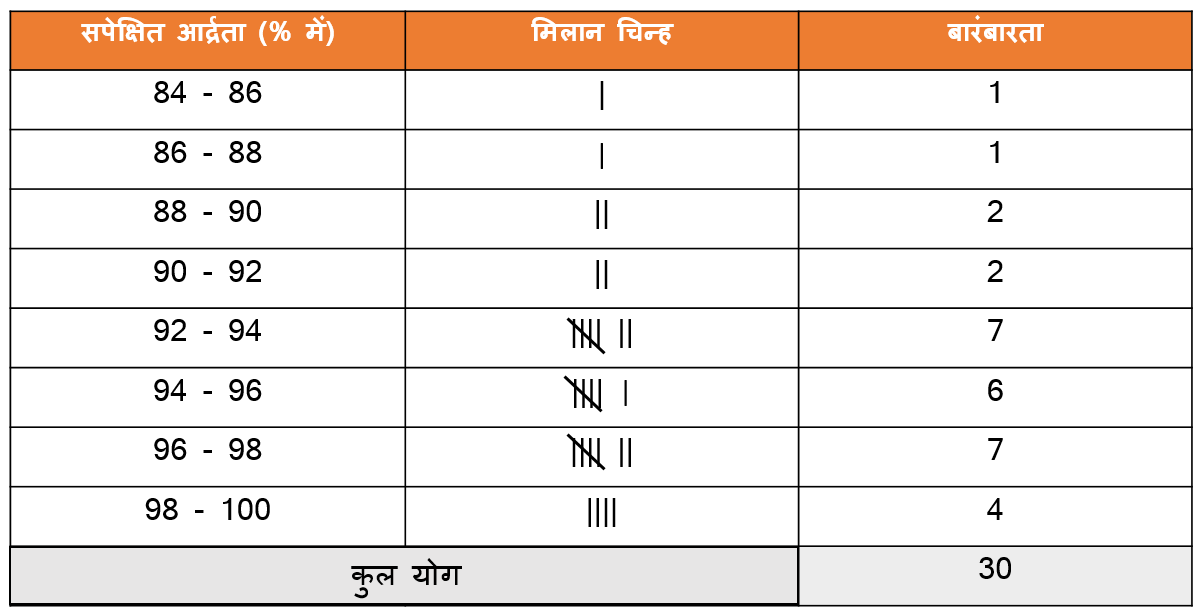
(ii) चूंकि सारणी मे देख सकते हैं की आर्द्रता बढ़ रही हैं अतः ये आंकड़े वर्षा ऋतु से संबंधित होंगे।

(iii) आंकड़ों का परिसर

=

अधिकतम आर्द्रता

-

न्यूनतम आर्द्रता

= 99.2 - 84.9

= 14.3

Learn more

उदाहरण 4

30 बच्चों से यह पूछा गया की पिछले सप्ताह उन्होंने कितने घंटो तक टेलीविज़न के प्रोग्राम देखे, प्राप्त परिणाम ये रहे है:

1, 6, 2, 3, 5, 12, 5, 8, 4, 8, 10, 3, 4, 12, 2, 8, 15, 1, 17, 6, 3, 2, 8, 5, 9, 6, 8, 7, 14, 12

(i) वर्ग - चौड़ाई 5 लेकर और एक वर्ग अंतराल लेकर इन आंकड़ों की एक वर्गीकृत बारंबारता बंटन सारणी बनाइये।
(ii) कितने बच्चो ने सप्ताह में 15 या अधिक घंटो तक टेलीविज़न देखा?

(i) दिए गए आंकड़ों में न्यूनतम तथा अधिकतम टेलीविज़न देखने का समय क्रमश: 1 घंटा और 17 घंटे हैं। वर्ग - चौड़ाई 5 लेना है।
अतः वर्ग चौड़ाई 5 लेने पर सामान आकार के वर्ग अंतराल $0 - 5$ , $5 - 10$ , $10 - 15$ और $15 - 20$ होंगे।

अतः वर्गीकृत बारंबारता बंटन सारणी:

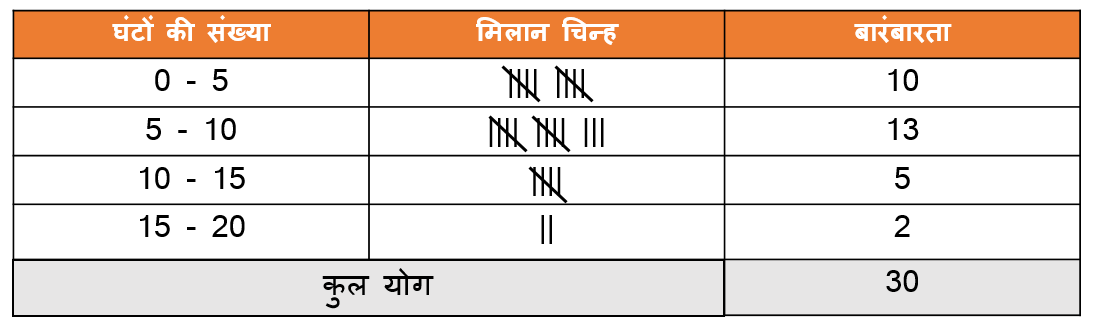
(ii) सारणी से स्पष्ट हैं की, 2 बच्चे सप्ताह में 15 या अधिक घंटे टेलीविज़न देखते हैं।

Learn more

उदाहरण 5

एक वर्ष विशेष में बिहार राज्य के प्राथमिक स्कूल के अध्यापकों की आयु (वर्षो में) का बंटन निम्नलिखित है:

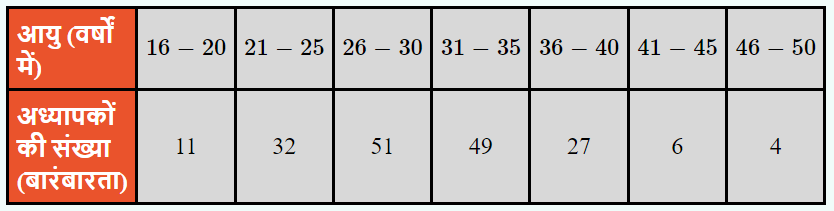
(i) पहले वर्ग-अंतराल की निम्न सीमा लिखे।
(ii) दूसरे वर्ग-अंतराल की वास्तविक ऊपरी सीमा लिखिए।
(iii) चौथे वर्ग-अंतराल की वर्ग सीमाएं ज्ञात करे।
(iv) सातवे वर्ग-अंतराल का वर्ग चिह्न ज्ञात करे।

(i) दिए गए सारणी से स्पष्ट हैं की $16 - 20$ पहला वर्ग - अंतराल हैं जिसमे 16 निम्न सीमा हैं।

(ii) यहाँ, वर्ग - अंतराल $(21 - 25)$ असंतत (समावेशी में) हैं, अतः इसे संतत (अपवर्जी ) मे बदलते हैं,
यहाँ $16 - 20$ और $21 - 25$ में, 20 और 21 के बीच 1 रिक्ति (Gap) हैं। रिक्ति (Gap) के आधे $(\frac{1}{2} = 0.5)$ को निम्न सीमा मे घटाना और उच्च सीमा मे जोड़ना होता है।

$∴$ दूसरा वर्ग - अंतराल $21 - 25$ में, निम्न सीमा $21 - 0.5 = 20.5$ और उच्च सीमा $25 + 0.5 = 25.5$ होगा।

अतः वास्तविक दूसरा वर्ग - अंतराल $20.5 - 25.5$ हैं जिसमे 25.5 वास्तविक ऊपरी सीमा हैं।

(iii) चौथे वर्ग - अंतराल की वर्ग सीमाएं $31 - 35$ हैं, जिसमे निम्न सीमा $31$ और उच्च सीमा $35$ हैं।

(iv) हम जानते हैं की, वर्ग - चिह्न $=$

उच्च सीमा

+

निम्न सीमा 2

सातवे वर्ग - अंतराल का वर्ग - चिह्न

= \frac{46 + 50}{2} = 48

Learn more

आंकड़ों का आलेखीय निरूपण

आंकड़ों को सरलता से समझने के लिए इन्हें विभिन्न प्रकार के चित्रों के माध्यम से प्रदर्शित किया जाता है। ठीक ढंग से बनाये गये चित्र या आलेख को देखते ही आंकड़ों के बारे में बहुत सारी सूचनायें मिल जाती हैं तथा चित्रों की सहायता से आंकड़ों का अध्ययन आसान हो जाता है।

यहाँ, हम दंड आलेख (Bar Graph), आयतचित्र (Histograms) और बारंबारता बहुभुज (Frequency Polygons) का अध्ययन करेंगे।

दंड आलेख (Bar Graph)

दंड आलेख आंकड़ों का एक चित्रीय निरूपण होता है जिसमें प्रायः एक अक्ष (मान लीजिए X - अक्ष) पर एक चर को प्रकट करने वाले एक समान चौड़ाई के दंड खींचे जाते हैं जिनके बीच में बराबर - बराबर दूरियाँ छोड़ी जाती हैं और चर के मान दूसरे अक्ष (मान लीजिए Y - अक्ष) पर दिखाए जाते हैं और दंडों की ऊँचाइयाँ, चर के मानों पर निर्भर करती हैं।

उदाहरण से समझते हैं:
किसी वर्ष विभिन्न राज्यों में प्रति हेक्टर औसत कृषि उपज (kg में) आंकड़े नीचे सारणी में दिया गया है। उन्हें दंड आलेख में दिखाएँ।

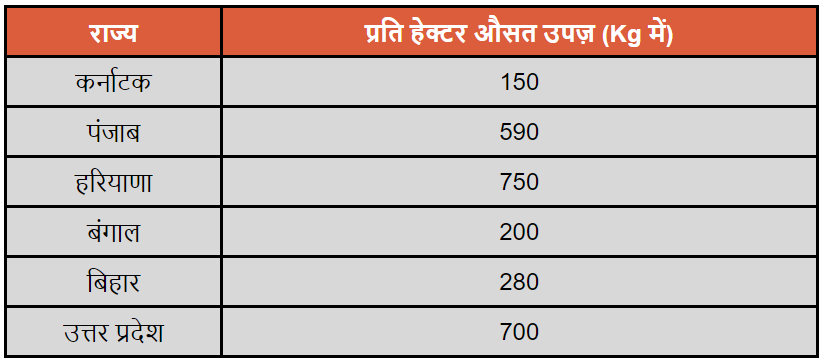
ocr_image

दिए गए आंकड़ों को दंड आलेख मे व्यक्त करते हैं -

सर्वप्रथम दो अक्ष बना लेते हैं

X

- अक्ष (क्षैतिज अक्ष) और

Y

- अक्ष (ऊर्ध्वाधर अक्ष ),

Y

- अक्ष पर प्रति हेक्टर औसत कृषि उपज को और

X

- अक्ष पर राज्यों को दर्शाते हैं।

यहाँ दिए गए आंकड़ों में महत्तम उपज 750 Kg और न्यूनतम 150 Kg हैं। अतः

Y

- अक्ष पर एक पैमाना लेते हैं,

1 c m = 100

Kg और 0 से 800 kg तक को

Y

- अक्ष पर दर्शाते हैं।

Y

- अक्ष पर बराबर दूरियों पर क्रमश: 100, 200, 300,............800 लिया गया हैं तथा

X

- अक्ष पर एक उपर्युक्त पैमाना लेकर राज्यों की बीच की दूरी को बराबर रखा गया हैं।

स्पष्ट हैं की, कर्नाटक के लिए उपज 150 Kg है, इसलिए कर्नाटक लिखे हुए आयत की ऊँचाई 100 और 200 अंकित बिंदु के बीच (चूंकि

1 c m = 100

kg अतः

150

k g

= 1.5 c m

) होगा। इसी प्रकार, हरियाणा के लिए उपज 750 kg हैं अतः हरियाणा लिखे हुए आयत की ऊँचाई 700 और 800 अंकित बिंदु के बीच होगा, इसी प्रकार अन्य राज्यों की उपज दिखाने वाले आयतों (दंडों) की ऊँचाइयाँ ली गई हैं।

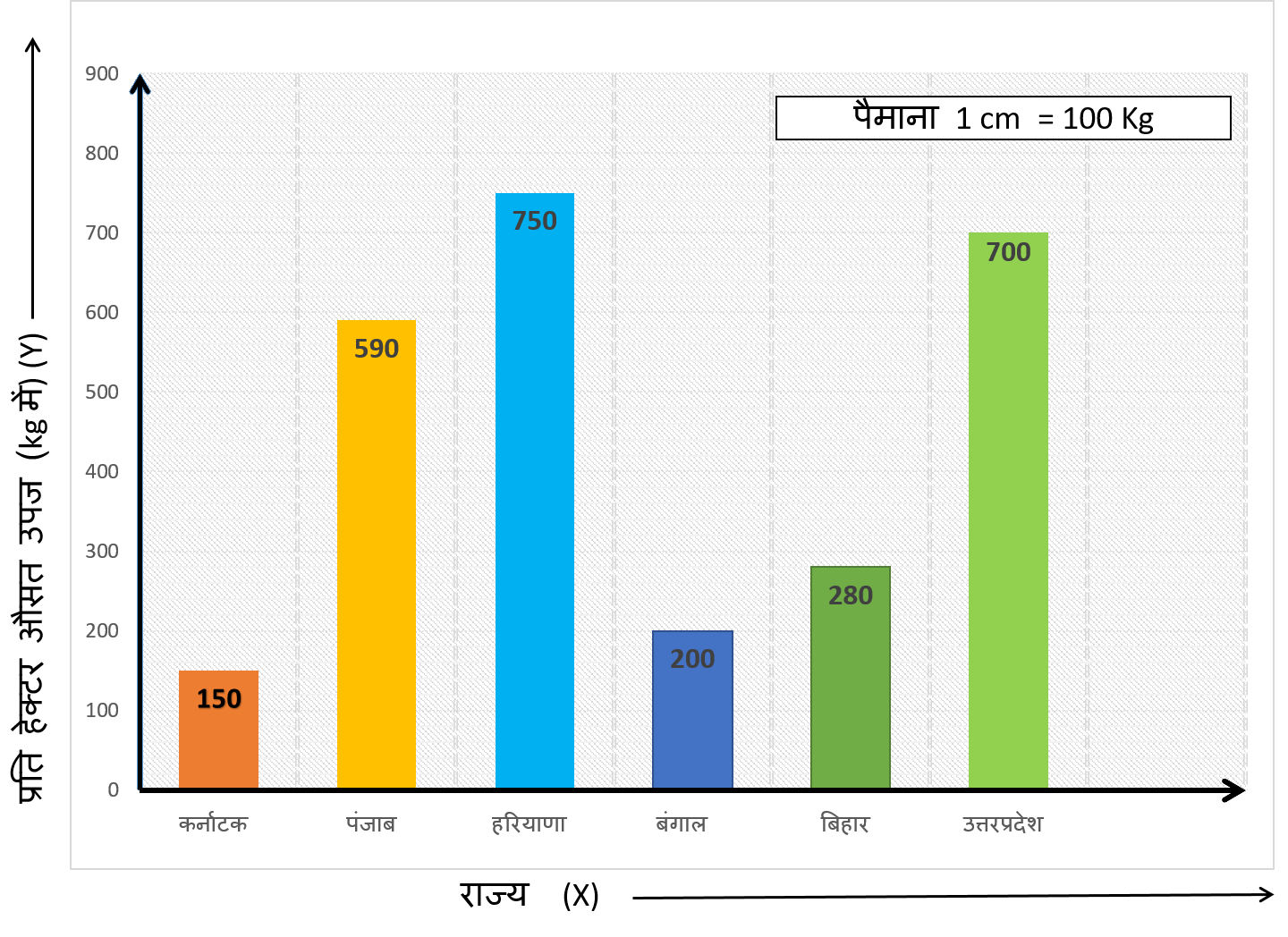
ocr_image

निष्कर्ष:- आलेख से स्पष्ट है कि प्रति हेक्टर औसत उपज हरियाणा में सर्वाधिक एवं कर्नाटक में सबसे कम रहा है, क्योंकि हरियाणा को दिखाने वाला दंड सबसे लम्बा एवं कर्नाटक वाला दंड सबसे छोटा है।

आयतचित्र (Histograms)

संतत वर्गीकृत (अपवर्जी विधि में वर्गीकृत) आंकड़ों को प्रदर्शित करने के लिए आयतचित्र का प्रयोग किया जाता है। आयतचित्र खींचने के लिए वर्ग - अंतराल को

X

- अक्ष पर तथा संगत बारंबारताओं को

Y

- अक्ष पर लिया जाता है। आयतचित्र में किसी आयत की चौड़ाई वर्ग विस्तार के बराबर होती है तथा उसकी ऊँचाई इतनी होती है की आयत का क्षेत्रफल उस वर्ग विशेष की बारंबारता को निरूपित करे।

उदाहरण से समझते हैं: दिए गए बारंबारता बंटन सारणी, जिसमें एक कक्षा के 36 विद्यार्थियों के भार दिए गए हैं। आंकड़ों को आलेखीय रूप में निरूपित कीजिए।

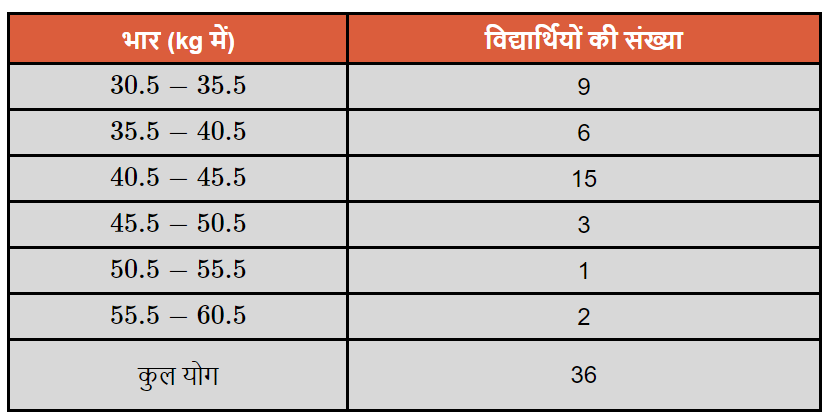
ocr_image

यहाँ, दिए गए आंकड़े संतत है क्योंकि यहाँ वर्ग की उच्च (ऊपरी) सीमा तथा अगले वर्ग की निम्न सीमा बराबर है।
अब, जैसा की हम जानते हैं की, वर्ग-अंतराल को

X

- अक्ष (क्षैतिज अक्ष) पर और संगत बारंबारताओं को

Y

- अक्ष (ऊर्ध्वाधर अक्ष) पर लिया जाता हैं।

चूंकि पहला वर्ग अंतराल

30.5

से प्रारंभ हो रहा है न कि शून्य से, इसलिए एक निकुंच (kink) का चिह्न बनाकर हम आलेख पर दर्शा सकते हैं।

एक उपर्युक्त पैमाना लेकर भार को

X

- अक्ष (क्षैतिज अक्ष) पर निरूपित करते हैं और विद्यार्थियों की संख्या (बारंबारता) को

Y

- अक्ष (ऊर्ध्वाधर अक्ष) पर निरूपित करते हैं।

पैमाना:-

X

- अक्ष पर

1 c m = 5 k g

तथा

Y

- अक्ष पर

1 c m = 2

विद्यार्थियों की संख्या

अब हम वर्ग अंतराल के अनुसार समान चौड़ाई और संगत वर्ग अंतरालों की बारंबारताओं को लंबाइयाँ मानकर आयत (या आयताकार) दंड बनाते हैं।

यहाँ, वर्ग अंतराल

30.5 - 35.5

का आयत

1 c m

की चौड़ाई और

4.5 c m

की लंबाई वाला आयत होगा।

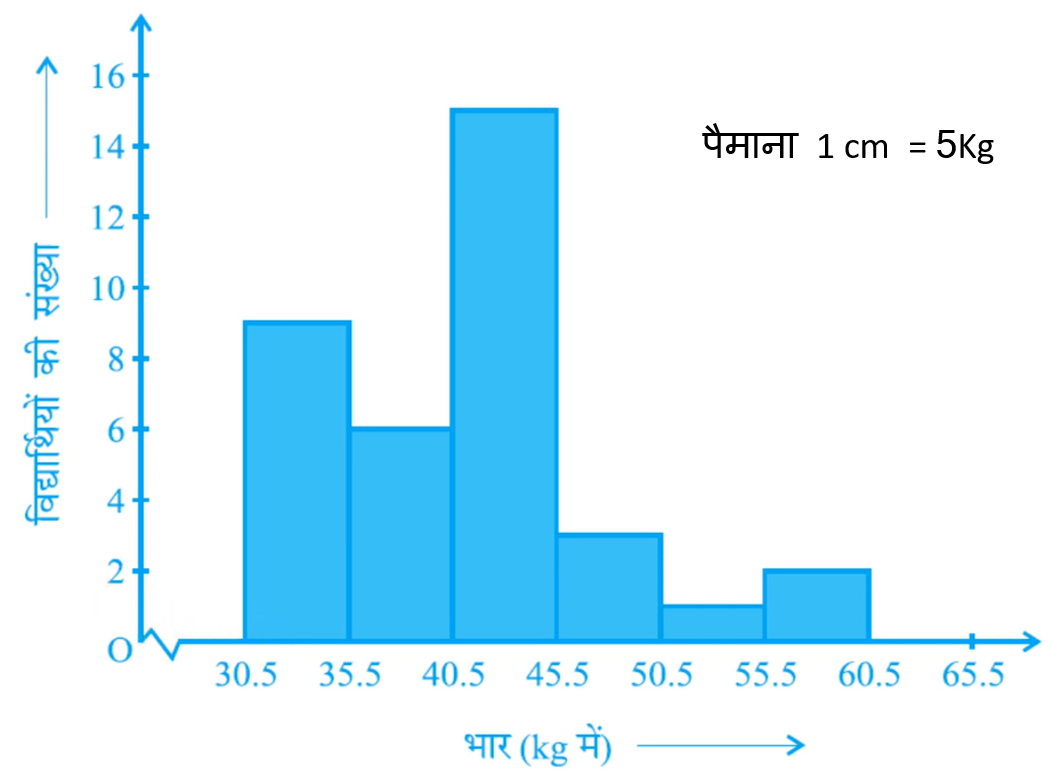
ocr_image

यहाँ क्रमागत आयतों के बीच कोई रिक्त स्थान (रिक्ति) नहीं है, इसलिए परिणामी आलेख एक ठोस आकृति के समान दिखाई दे रहा हैं। इस आलेख को आयतचित्र (histogram) कहा जाता है, जो कि संतत वर्गों वाले वर्गीकृत बारंबारता बंटन का एक आलेखीय निरूपण है। साथ ही, दंड आलेख के विपरीत, इसकी रचना में दंड की चौड़ाई की एक महत्वपूर्ण भूमिका होती है।

यहाँ खड़े किए गए आयतों के क्षेत्रफल संगत बारंबारताओं के समानुपाती होते हैं क्योंकि सभी आयतों की चौड़ाईयाँ सामान हैं इसलिए आयतों की लंबाइयाँ बारंबारताओं के समानुपाती होती हैं।

Note:-

यदि दिए गए बारंबारता बंटन में वर्ग - अंतराल की चौड़ाई अलग - अलग हो, तो सर्वप्रथम हम निम्न सूत्र का प्रयोग करके बारंबारता को समायोजित करेंगे।
किसी वर्ग की समायोजित बारंबारता

=

न्यूनतम वर्ग - चौड़ाई दिए गए वर्ग की वर्ग - चौड़ाई

\times

दिए गए वर्ग की बारंबारता

इसका अध्ययन आगे उदाहरण में करेंगे।

यदि दिया गया आँकड़ा अवर्गीकृत हो, तो इन आंकड़ों से इस प्रकार बारंबारता सारणी बनाते हैं कि वर्ग - अंतराल अपवर्जी (संतत) हो। यदि दिए गए आंकड़ों का वर्ग - अंतराल समावेशी (असंतत) हो, तो वर्ग - चिह्न से वर्ग - अंतरालों को अपवर्जी (संतत) में परिवर्तित करते हैं।

वर्ग अंतरालों को आधार (चौड़ाई) तथा संगत बारंबारता को ऊँचाई मानकर आयत बनाते हैं।

यदि वर्ग अंतराल की निम्नतम सीमा बड़ी संख्या हो तो

X

- अक्ष पर निकुंच (kink) का चिह्न बनाकर या अक्ष में एक विच्छेद दिखाकर, इसे हम आलेख पर दर्शा सकते हैं।

बारंबारता बहुभुज (Frequency Polygons)

दिये गये आंकड़ों का बारंबारता बहुभुज वह बहुभुज है जो इन आंकड़ों के आयतचित्र के आयतों की ऊपरी भुजाओं के मध्य - बिंदुओं को क्रम से रेखाखंड द्वारा मिलाने से बनता है।

उदाहरण से समझते हैं: नीचे दिये गए आयत चित्र का बारंबारता बहुभुज बनाइए:
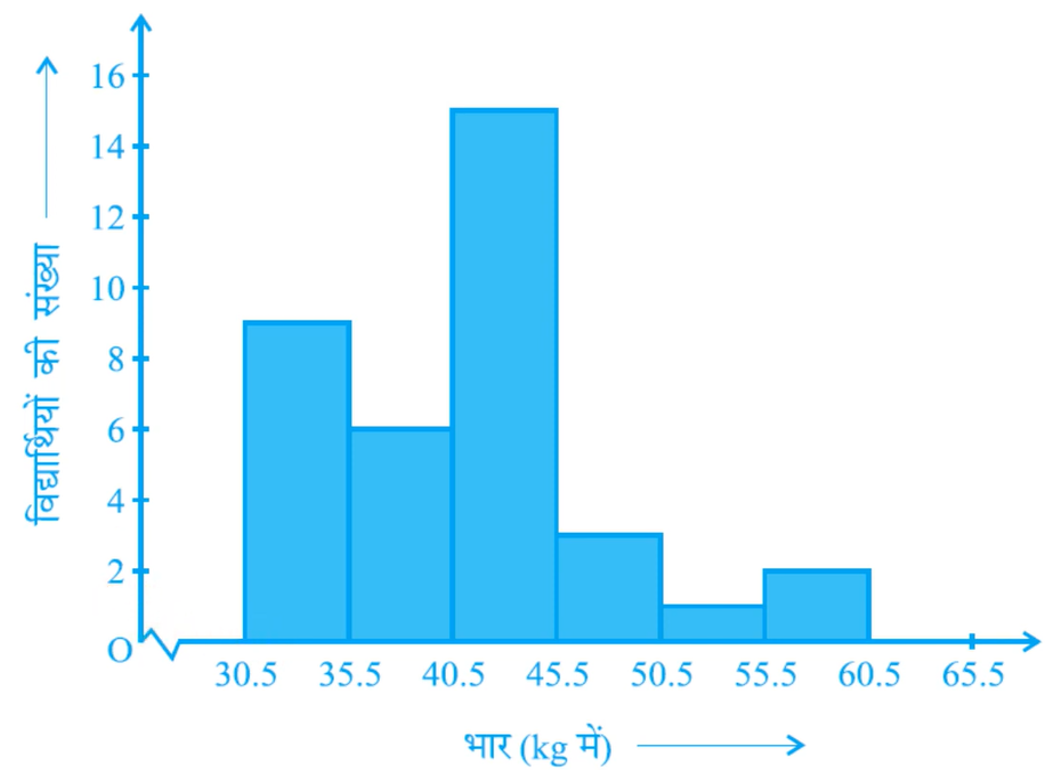
ocr_image

आयतचित्र के संगत आयतों की ऊपरी भुजाओं के मध्य - बिंदुओं को रेखाखंडों से जोड़ देते हैं और इन मध्य - बिंदुओं को

B

C

D

E

F

और

G

से चिन्हित करते हैं। जब इन मध्य - बिंदुओं को हम रेखाखंडों से जोड़ देते हैं, तो हमें आकृति

B C D E F G

प्राप्त होती है बहुभुज को पूरा करने के लिए यहाँ हम यह मान लेते हैं कि

30.5 - 35.5

के पहले और

55.5 - 60.5

के बाद शून्य बारंबारता वाले एक - एक वर्ग - अंतराल हैं और इनके मध्य - बिंदु क्रमशः

A

और

H

हैं।

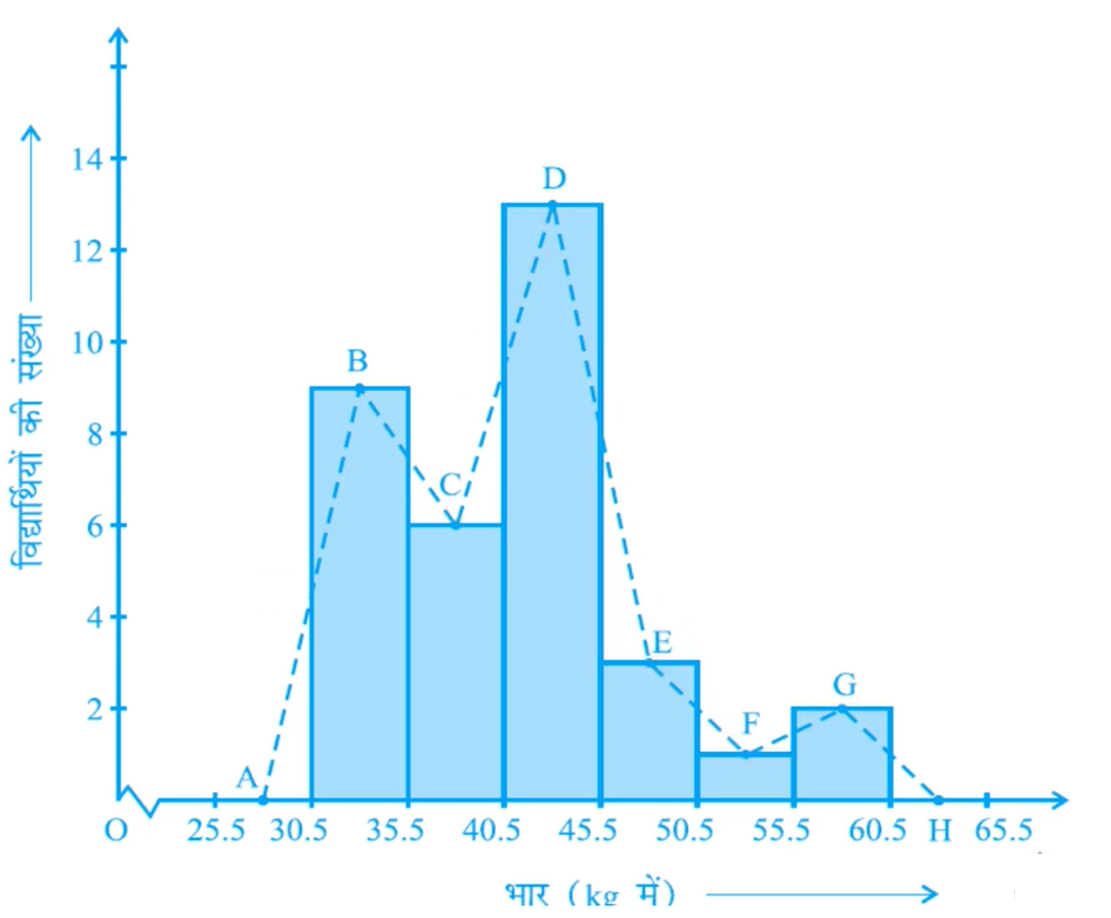
अतः बारंबारता बहुभुज

A B C D E F G H

है।

आयतचित्र बनाए बिना ही बारंबारता बहुभुजों को स्वतंत्र रूप से बनाया जा सकता है। इसके लिए हमें आंकड़ों में प्रयुक्त वर्ग अंतरालों के मध्य - बिंदुओं की आवश्यकता होती है। वर्ग अंतरालों के इन मध्य - बिंदुओं को वर्ग - चिह्न (class-marks) कहा जाता है।

वर्ग - चिह्न

=

उच्च सीमा

+

निम्न सीमा 2

जैसे:- वर्ग - अंतराल

140 - 150

की ऊपरी सीमा 150 और निम्न सीमा 140 है।

= \frac{150 + 140}{2} = \frac{290}{2} = 145

इसी प्रकार, हम अन्य वर्ग अंतरालों के वर्ग - चिह्न ज्ञात कर सकते हैं और वर्ग चिह्न और बारंबारताओं की सहायता से बारंबारता बहुभुज बनाया जा सकता हैं, जिसे हम उदाहरण में देखेंगे।

OMR (One Minute Revision)

दंड आलेख:- यह आंकड़ों को आयताकार दंड के रूप में प्रस्तुत करने का सबसे आसान तरीका है प्रत्येक दंड की चौड़ाई समान होनी चाहिए तथा दंड के बीच का स्थान भी समान होना चाहिए और दंड की ऊंचाई दर्शाए जाने वाले संख्यात्मक आंकड़े के अनुसार होनी चाहिए।

आयतचित्र:- संतत वर्गीकृत आंकड़ों को प्रदर्शित करने के लिए आयतचित्र का प्रयोग किया जाता है। यदि दिया गया आँकड़ा अवर्गीकृत हो, तो इन आंकड़ों से इस प्रकार बारंबारता सारणी बनायें कि वर्ग- अंतराल अपवर्जी (संतत) हो। वर्ग अंतरालों को आधार (चौड़ाई) तथा संगत बारंबारता को ऊँचाई मानकर आयत बनाते हैं।

बारंबारता बहुभुज:- आयतचित्र बनाए बिना ही बारंबारता बहुभुजों को स्वतंत्र रूप से बनाया जा सकता है। इसके लिए हमें आंकड़ों में प्रयुक्त वर्ग अंतरालों के मध्य - बिंदुओं की आवश्यकता होती है। वर्ग अंतरालों के इन मध्य बिंदुओं को वर्ग-चिह्न (class-marks) कहा जाता है।

उदाहरण 6

एक राज्य के विधान सभा के चुनाव में विभिन्न राजनैतिक पार्टीयों द्वारा जीती गई सीटों के परिणाम नीचे दिए गए है :

(i) मतदान के परिणामो को निरूपित करने वाला दंड आलेख खींचिए।
(ii) किस राजनैतिक पार्टी ने अधिकतम सीटें जीती है?

(i) दिए गए आंकड़ों को दंड आलेख मे व्यक्त करते हैं:

सर्वप्रथम दो अक्ष बना लेते हैं $X$ - अक्ष (क्षैतिज अक्ष) और $Y$ - अक्ष (ऊर्ध्वाधर अक्ष) तथा $X$ - अक्ष पर राजनैतिक पार्टियों को कोई भी पैमाना लेकर निरूपित कर सकते हैं, यहाँ सभी दंड समान चौड़ाई के और उनकी बीच की दूरी समान होनी चाहिए।

$Y$ - अक्ष पर जीती गई सीटों को एक पैमाना लेकर निरूपित करते हैं:

यहाँ, अधिकतम सीटें 75 हैं, इसलिए पैमाना 1 cm = 15 सीटें ले सकते हैं।

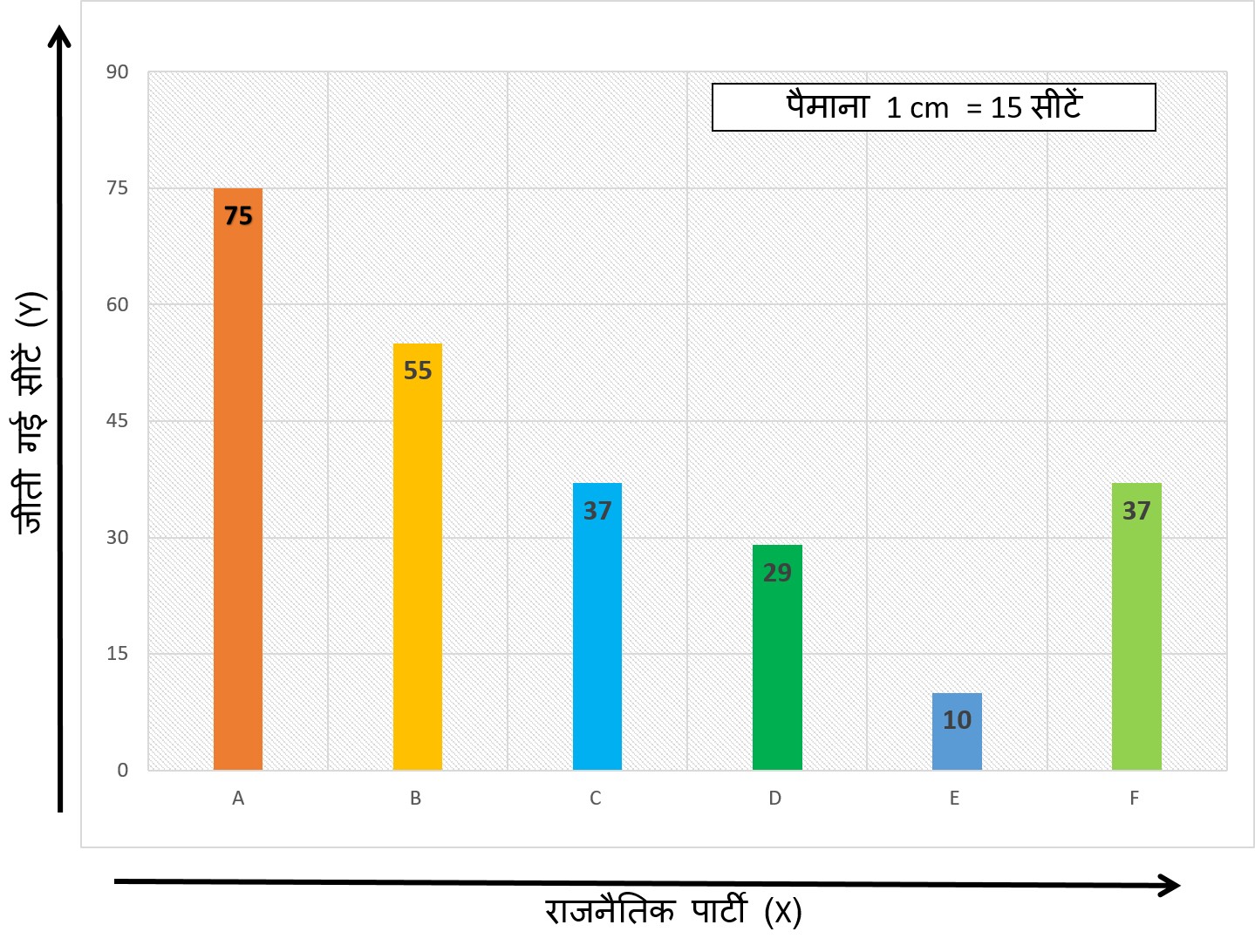
(ii) चूंकि दंड A की ऊँचाई सबसे अधिक 75 हैं अतः स्पष्ट हैं की राजनैतिक पार्टी A ने सबसे अधिक 75 सीटें जीती हैं।

Learn more

उदाहरण 7

चित्र में दर्शाये गये दंड आलेख को समझकर निम्न प्रश्नो के उत्तर दो :

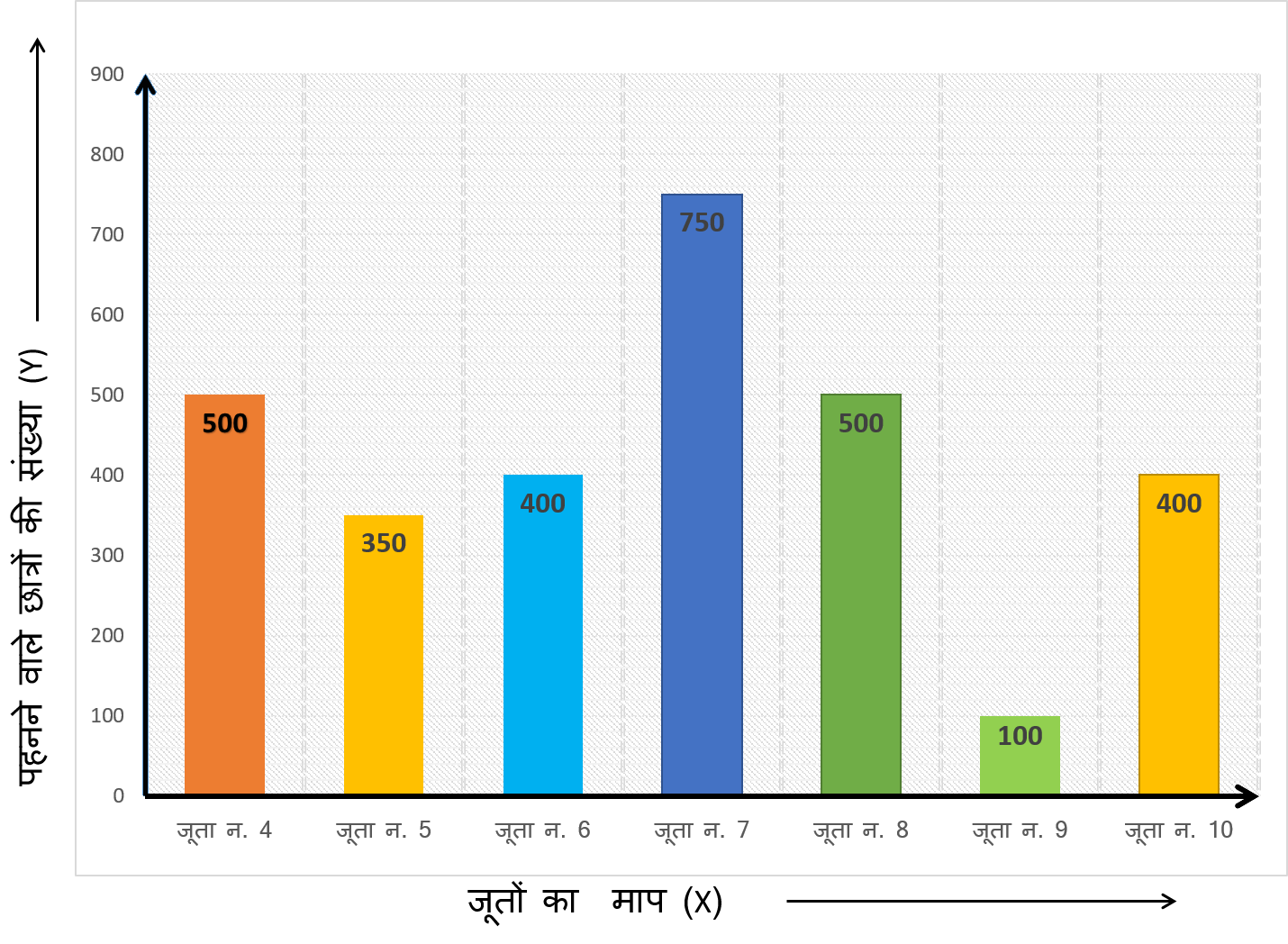
(i) दंड आलेख के द्वारा दी गई सूचनायें क्या है ?
(ii) विद्यार्थियों के द्वारा पहने हुए जूतों के माप क्या है ?
(iii) 6 नम्बर का जूता पहनने वाले विद्यार्थियों की संख्या कितनी है ?
(iv) अधिकतर विद्यार्थियों के द्वारा किस नम्बर के जूते पहने जाते है ?
(v) सबसे कम विद्यार्थियों के द्वारा पहने गये जूते का नम्बर क्या है ?
(vi) सही या गलत बताओ :
10 नम्बर माप का जूता पहनने वाले विद्यार्थियों की संख्या, 9 नम्बर माप का जूता पहनने वाले विद्यार्थियों की संख्या के तीन गुना से कम है।

स्पष्ट है कि, विद्यार्थियों की कुल संख्या $= 500 + 350 + 400 + 750 + 500 + 100 + 400 = 3000$ हैं।

(i) दिया गया दंड आलेख कुल 3000 चुने गये विद्यार्थियों में से विभिन्न माप के जूते पहनने वाले विद्यार्थियों को निरूपित करता है।

(ii) विद्यार्थियों के द्वारा 4, 5, 6, 7, 8, 9 और 10 नम्बर माप के जूते पहने जाते है।

(iii) 6 नम्बर माप का जूता पहनने वाले विद्यार्थियों की संख्या 400 है।

(iv) 7 नम्बर माप का जूता सबसे अधिक विद्यार्थियों द्वारा पहना जाता है ऐसे विद्यार्थियों की संख्या 700 है।

(v) 9 नम्बर माप का जूता सबसे कम विद्यार्थियों द्वारा पहना जाता है ऐसे विद्यार्थियों की संख्या 100 है।

(vi) 10 नम्बर माप का जूता पहने वाले विद्यार्थियों की संख्या 400 है और 9 नम्बर माप का जूता पहनने वाले विद्यार्थियों की संख्या 100 है। अतः 10 नंबर माप का जूता पहनने वाले विद्यार्थियों की संख्या का तीन गुना अधिक हैं 9 नम्बर माप का जूता पहनने वाले विद्यार्थियों की संख्या से। अतः दिया गया कथन गलत है।

Learn more

उदाहरण 8

100 व्यक्तियों की (cm में) का बंटन निम्न प्रकार है:

इस बारंबारता बंटन को आयत चित्र में प्रदर्शित करें।

यहाँ दिया गया आँकड़ा संतत है क्योंकि यहाँ वर्ग की उच्च (ऊपरी) सीमा तथा अगले वर्ग की निम्न सीमा बराबर है।

अब, जैसा की हम जानते हैं, वर्ग - अंतराल को $X$ - अक्ष (क्षैतिज अक्ष) पर और संगत बारंबारताओं को $Y$ - अक्ष (ऊर्ध्वाधर अक्ष) पर लिया जाता हैं।

चूंकि पहला वर्ग अंतराल $145$ से प्रारंभ हो रहा है न कि शून्य से, इसलिए एक निकुंच (kink) का चिह्न बनाकर हम आलेख पर दर्शा सकते हैं।

पैमाना (स्केल) माना की $X$ - अक्ष पर $1 c m = 10$
तथा $Y$ - अक्ष पर $1 c m = 5$ बारंबारता

अब हम वर्ग अंतराल के अनुसार समान चौड़ाई और संगत वर्ग अंतरालों की बारंबारताओं को लंबाइयाँ मानकर आयत (या आयताकार) दंड बनाते हैं।

अतः 100 व्यक्तियों की लम्बाइयों के बारंबारता बंटन का आयतचित्र:

Learn more

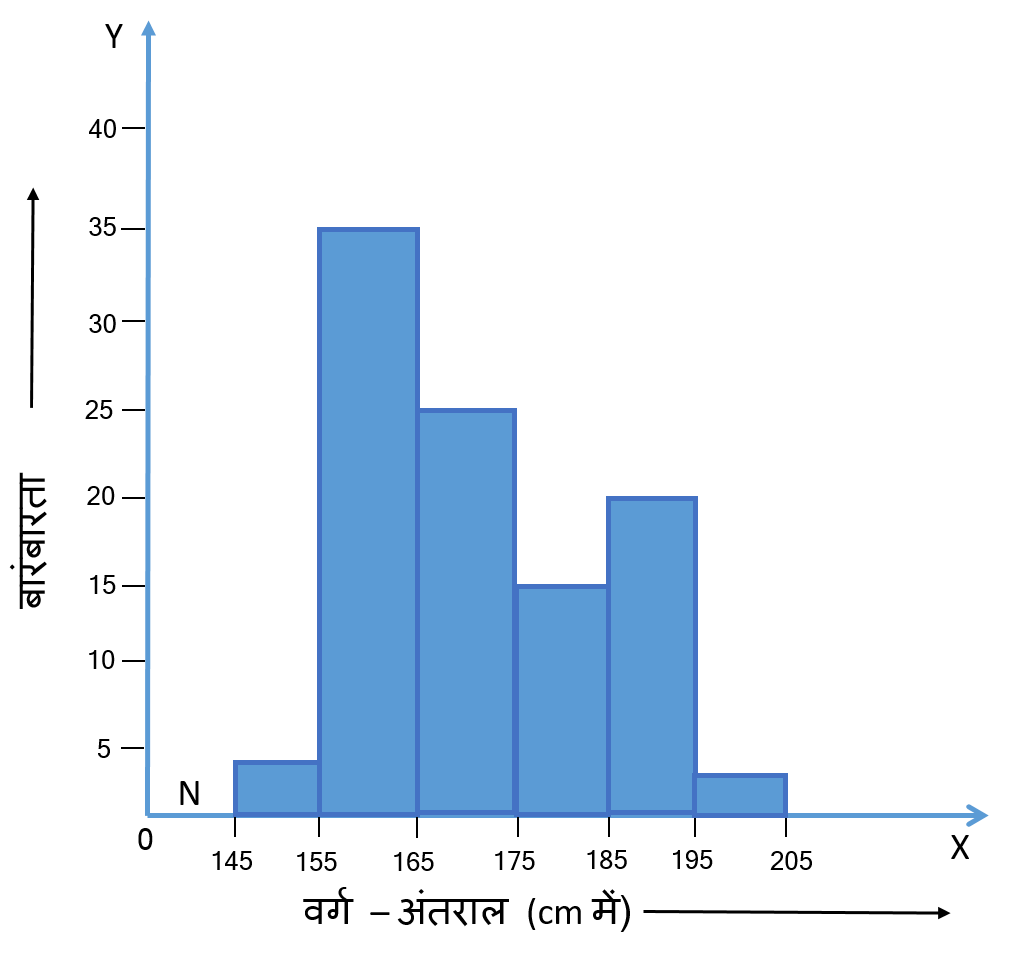
उदाहरण 9

एक स्थानीय टेलीफोन निर्देशिका से 100 कुलनाम (Surname) यादृच्छया लिए गए और उनसे अंग्रेजी वर्णमाला के अक्षरों की संख्या का निम्न बारंबारता बंटन प्राप्त किया गया :

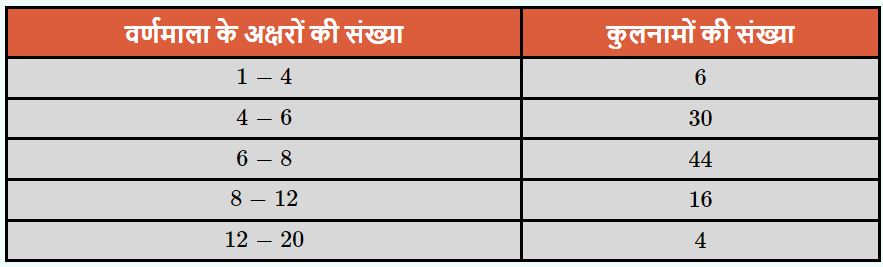
(i) दी गई सूचनाओं को निरूपित करने वाला एक आयतचित्र खींचिए।
(ii) वह वर्ग - अंतराल बताइए जिसमें अधिकतम संख्या में कुलनाम है।

(i) हम जानते हैं कि आयतों के क्षेत्रफल आयतचित्र में बारंबारताओं के समानुपाती होते हैं। यहाँ दिए गए बारंबारता वितरण में आयतों की चौड़ाइयाँ बदल रही हैं इसलिए आयतों की लंबाइयों में कुछ परिवर्तन की आवश्यकता है, जिससे क्षेत्रफल पुनः बारंबारताओं के समानुपाती हो जाए।

अतः सर्वप्रथम हम सूत्र का प्रयोग करके समायोजित बारंबारता की गणना करते हैं।

किसी वर्ग की समायोजित बारंबारता $=$

न्यूनतम वर्ग - चौड़ाई दिए गए वर्ग की वर्ग - चौड़ाई

\times

दिए गए वर्ग की बारंबारता

यहाँ न्यूनतम वर्ग - चौड़ाई 2 है।

∴

समायोजित बारंबारता से निम्न सारणी प्राप्त होती हैं:

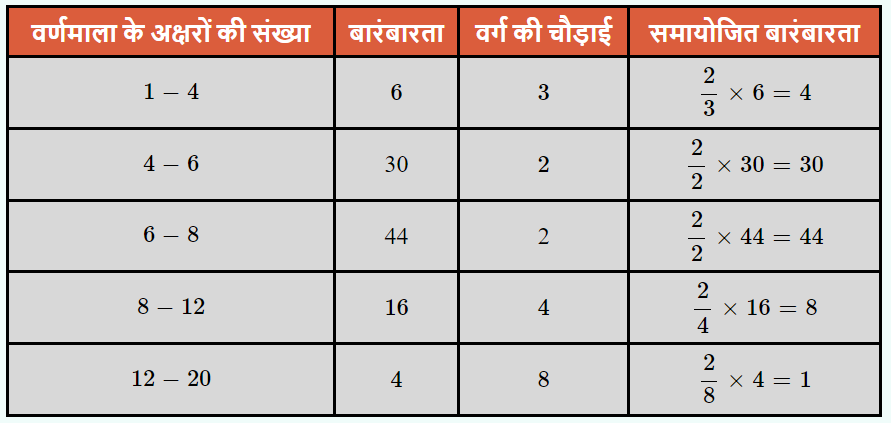
ocr_image

अब हम वर्ग - अंतराल को

X

- अक्ष पर तथा समायोजित बारंबारता को

Y

- अक्ष पर दर्शाने के लिए पैमाना लेते हैं:

माना की

X

- अक्ष पर

1 c m = 2

तथा

Y

- अक्ष पर

1 c m = 5

अब वर्ग - अंतराल को आधार मानते हुए और समायोजित बारंबारता को ऊँचाई मानकर आयत खींचते है।
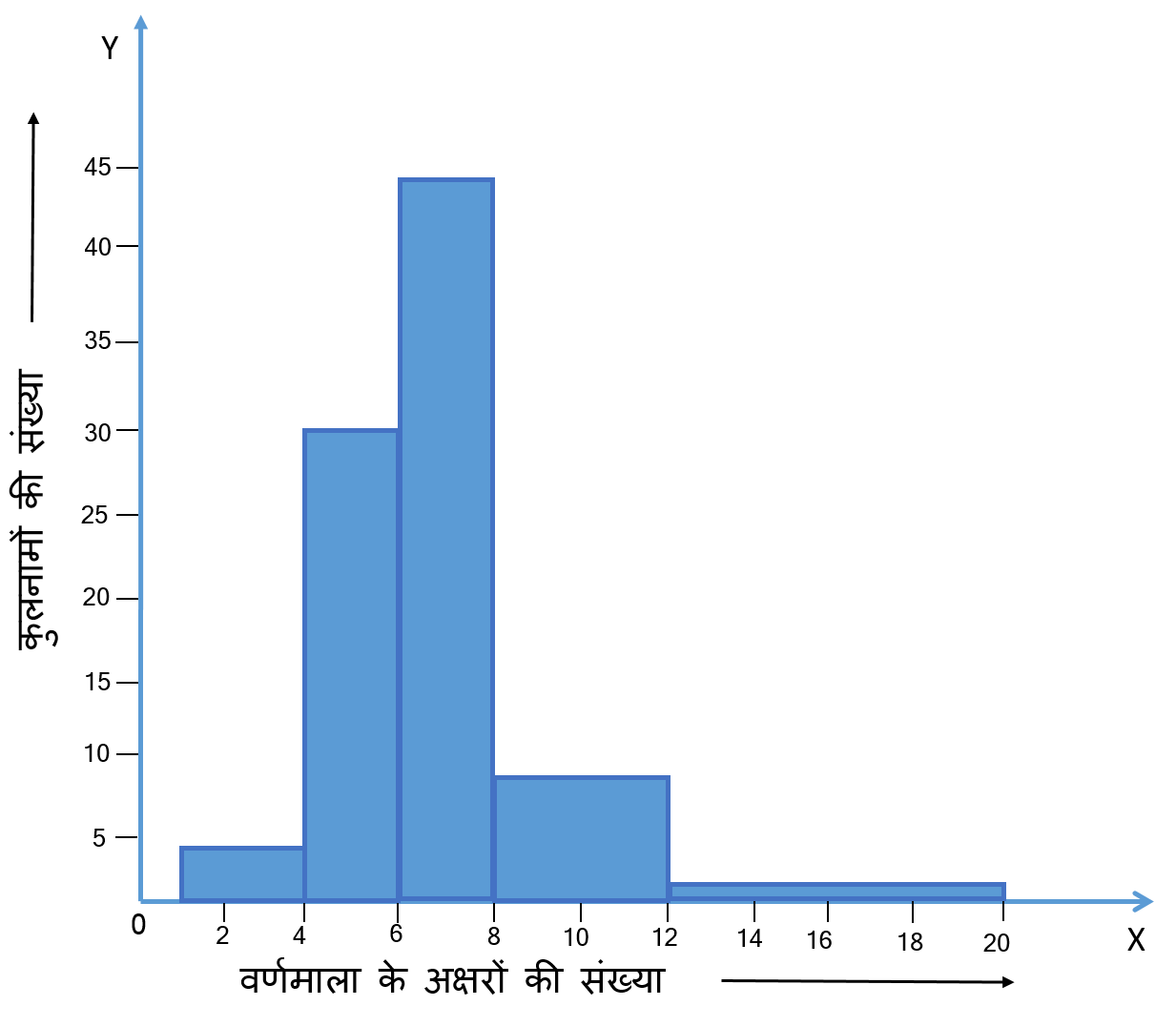
ocr_image

(ii) स्पष्ट हैं की अधिकतम (44 कुलनाम) कुलनाम वर्ग - अंतराल

6 - 8

में है।

Learn more

उदाहरण 10

एक नगर में निर्वाह खर्च सूचकांक का अध्ययन करने के लिए निम्नलिखित साप्ताहिक प्रेक्षण किए गए :

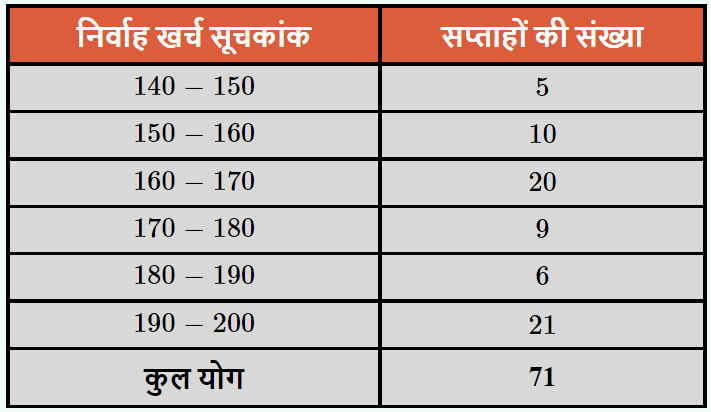
ऊपर दिए गए आंकड़ों का एक बारंबारता बहुभुज (आयतचित्र बनाए बिना) खीचिए।

हम जानते हैं की बिना आयतचित्र के बारंबारता बहुभुज खींचने के लिए दिए गए वर्ग अंतरालों का वर्ग - चिह्न निकालना होता हैं।

अतः वर्ग - चिह्न $=$

उच्च सीमा

+

निम्न सीमा 2

वर्ग अंतराल

140 - 150

की ऊपरी सीमा

150

और निम्न सीमा

140

है।

अतः, वर्ग - चिह्न

= \frac{140 + 150}{2} = 135

इसी प्रकार, हम अन्य वर्ग अंतरालों के वर्ग - चिह्न ज्ञात कर सकते हैं:

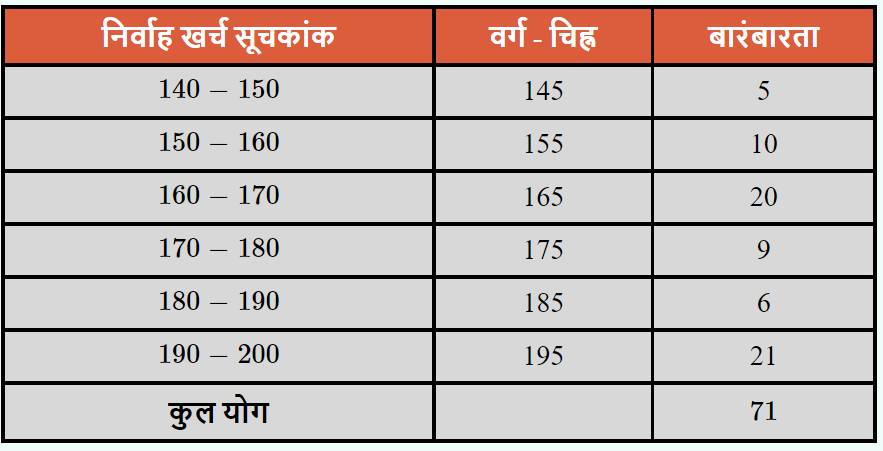
ocr_image

पैमाना:-

X

- अक्ष पर

1 c m = 10

Y

- अक्ष पर

1 c m = 2

अब क्षैतिज अक्ष (

X

- अक्ष) पर निर्वाह खर्च सूचकांक को और ऊर्ध्वाधर अक्ष (

Y

- अक्ष) पर बारंबारता (सप्ताहों की संख्या) को आलेखित करते हैं और फिर बिंदुओं B(145, 5), C(155, 10), D(165, 20), E(175, 9), F(185, 6) और G(195, 21) को चिन्हित करके उन्हें रेखाखंडों से मिलाकर हम बारंबारता बहुभुज खींच सकते हैं तथा शून्य बारंबारता के साथ वर्ग

130 - 140

(जो निम्नतम वर्ग

140 - 150

के ठीक पहले है) के वर्ग चिह्न के संगत बिंदु A(135, 0) को और G(195, 21) के तुरन्त बाद में आने वाले बिंदु H(205, 0) को आलेखित किया गया हैं। इसलिए परिणामी बारंबारता बहुभुज ABCDEFGH होगा:

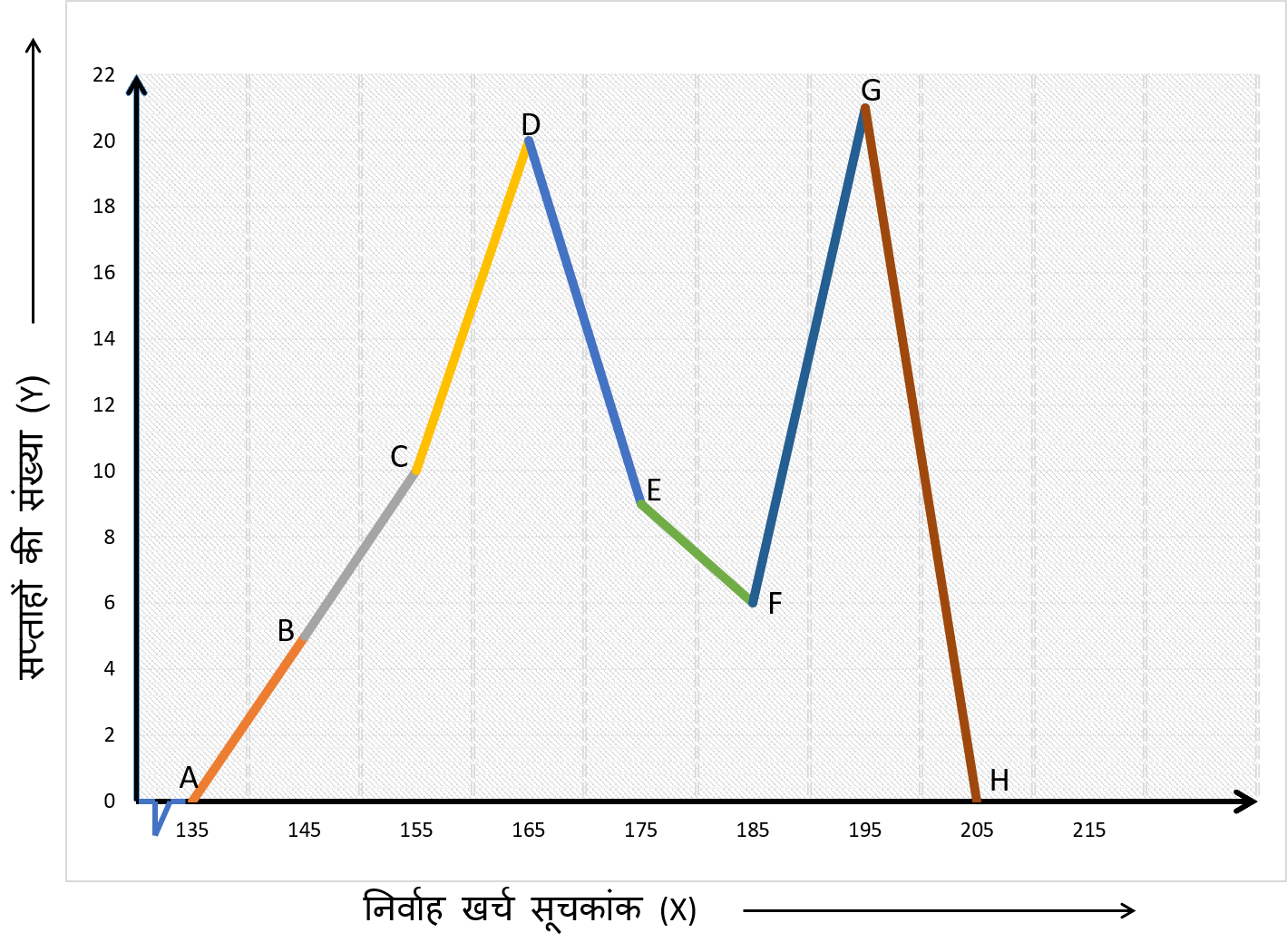
ocr_image

Learn more

उदाहरण 11

नीचे की दो सारिणियों में प्राप्त किए गए अंको के अनुसार दो सेक्शनों के विद्यार्थियों का बंटन दिया गया है :

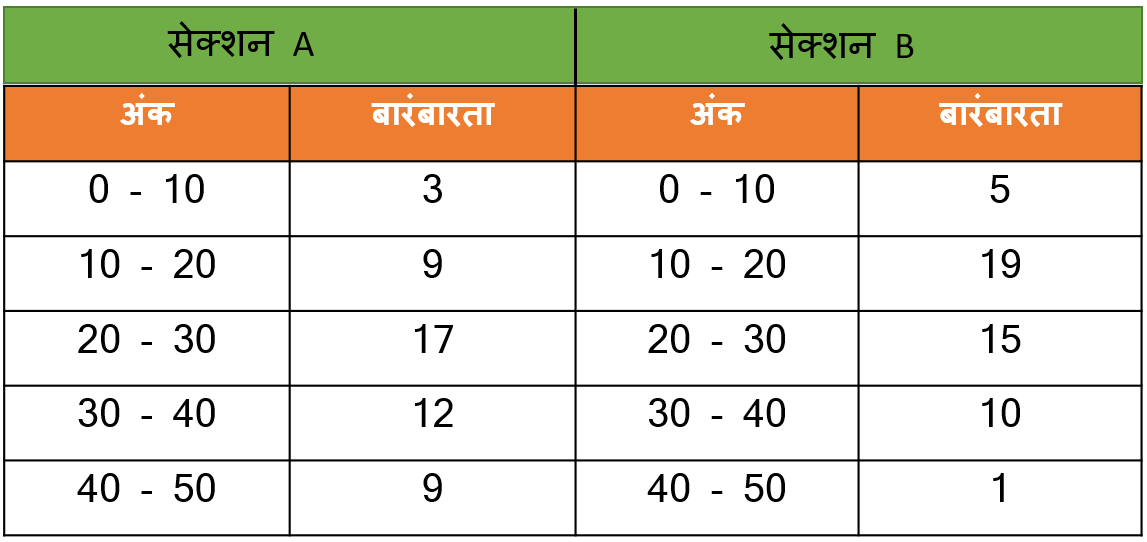
दो बारंबारता बहुभुजों की सहायता से एक ही आलेख पर दोनों सेक्शनों के विद्यार्थियों के प्राप्तांक निरूपित कीजिए। दोनों बहुभुजों का अध्ययन करके दोनों सेक्शनों के निष्पादनों की तुलना कीजिए।

हम जानते हैं की, बिना आयतचित्र के बारंबारता बहुभुज खींचने के लिए दिए गए वर्ग - अंतरालों का वर्ग - चिह्न निकालना होता हैं।

अतः वर्ग - चिह्न $=$

उच्च सीमा

+

निम्न सीमा 2

वर्ग अंतराल

0 - 10

की ऊपरी सीमा

10

और निम्न सीमा

0

है।

अतः, वर्ग - चिह्न

= \frac{10 + 0}{2} = 5

इसी प्रकार, हम अन्य वर्ग अंतरालों के वर्ग-चिह्न ज्ञात कर सकते हैं।

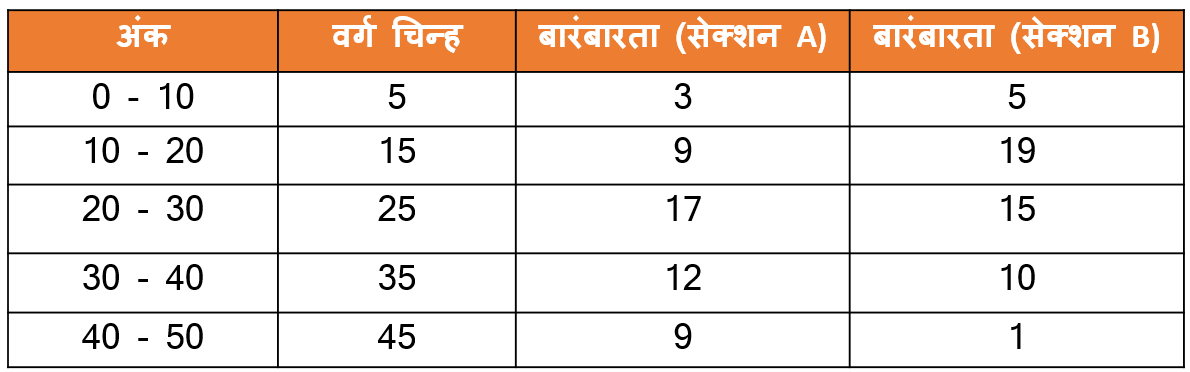
ocr_image

पैमाना:-

X

- अक्ष पर

1 c m = 5

अंक

Y

- अक्ष पर

1 c m = 2

बारंबारता

X

- अक्ष पर अंकों को तथा Y - अक्ष पर बारंबारता को दर्शाते है।
सेक्शन

A

के बारंबारता बहुभुज के लिए बिंदुओं (5,3), (15,9), (25,17), (35,12) और (45,9) को अंकित कर और इन बिंदुओं को रेखाखंड से मिलाते हैं।

सेक्शन

B

में बारंबारता बहुभुज के लिए हम बिंदुओं (5,5), (15,19), (25,15), (35,10) और (45,1) को अंकित कर और इन बिंदुओं को रेखाखंड से मिलाते है।

शून्य बारंबारता के साथ वर्ग

(- 10) - 0

(जो निम्नतम वर्ग

0 - 10

के ठीक पहले होगा) के वर्ग चिह्न के संगत बिंदु (

- 5

, 0) को और

50 - 60

(जो वर्ग

40 - 50

के ठीक बाद होगा) के वर्ग चिह्न के संगत बिंदु (55, 0) को आलेखित किया गया हैं।

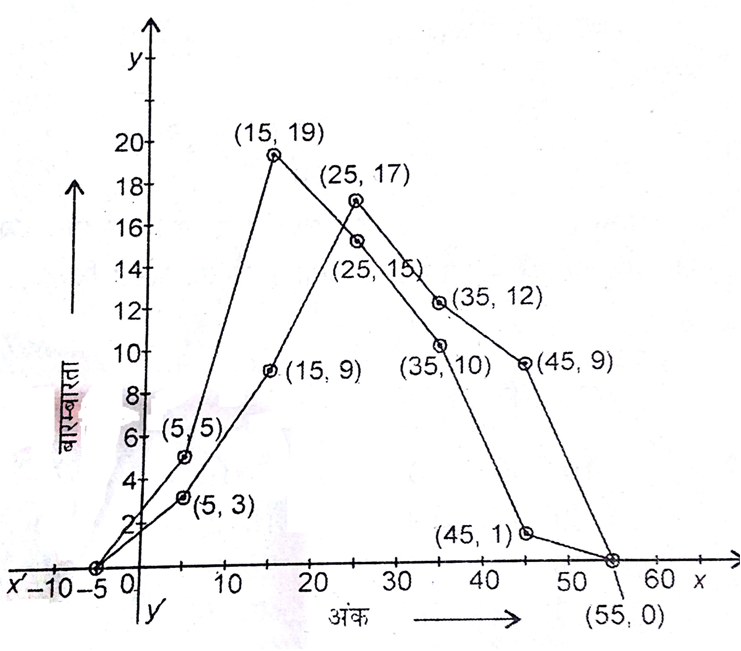
ocr_image

दोनों बहुभुजों के अध्ययन से बता सकते हैं कि सेक्शन

A

के विद्यार्थियों के प्राप्तांक, सेक्शन

B

के विद्यार्थियों के प्राप्तांक से बेहतर हैं।

Learn more

केन्द्रीय प्रवृत्ति के माप

केन्द्रिय प्रवृत्ति उस माप को कहते हैं, जो दिये गये आंकड़ों (Data) का प्रतिनिधित्व करता है। दूसरे शब्दों में, केन्द्रिय प्रवृत्ति के मापों से तात्पर्य औसत मान (Average Value) से होता है।

केन्द्रीय प्रवृत्ति का मापन तीन मापों (measures) द्वारा किया जाता है।
इन मापों को मध्यमान या माध्य (Mean), माध्यक (माध्यिका) (Median) तथा बहुलक (Mode) कहते हैं।

माध्य (Mean):- माध्य प्रेक्षणों की संख्या का औसत है। माध्य निकालने के लिए हमें प्रेक्षणों के मानों के योग को प्रेक्षणों की कुल संख्या से भाग देना होता हैं। इसे औसत मान भी कहते हैं। माध्य को $¯ x$ से प्रदर्शित करते हैं।

हम जानते हैं की,

अंकगणितीय माध्य =

प्रेक्षणों का योग प्रेक्षणों की संख्या

सूत्र :-(i) जब बंटन सरल या व्यक्तिगत हो:

मान लीजिए हमारे पास

x_{1}, x_{2}, x_{3}, ... . x_{n}

आंकड़े हैं:

जहाँ

n =

कुल आंकड़ों की संख्या है तब

माध्य

(¯ x) =

n \sum i = 1 x_{i}

n

यहाँ

i = 1, 2, 3, 4, 5, 6, 7, ... . n

इस प्रकार हम यह भी कह सकते हैं कि

¯ x = \frac{x_{1} + x_{2} + x_{3} + x_{4} + x_{5} + ... . . x_{n}}{n}

उदाहरण:- 5 व्यक्तियों से यह पूछा गया की अपने समुदाय के सामाजिक कार्य करने में वे एक सप्ताह में कितना समय देते हैं? उनका कहना था क्रमशः 10, 7, 13, 20 और 15 घंटे। एक सप्ताह में उनके द्वारा सामाजिक कार्य में लगाए समयों का माध्य (या औसत ) ज्ञात कीजिए।

हम जानते हैं की, माध्य

(¯ x) =

n \sum i = 1 x_{i}

n

यहाँ हमारे पास कुल 5 आंकड़ें हैं: 10, 7, 13, 20 और 15

अतः

n = 5

होगा तथा

i = 1, 2, 3, 4, 5

होगा।

\Rightarrow ¯ x = \frac{x_{1} + x_{2} + x_{3} + x_{4} + x_{5}}{5}

यहाँ

x_{1} = 10

x_{2} = 7

x_{3} = 13

x_{4} = 20

x_{5} = 15

तथा

n = 5

है

\Rightarrow ¯ x = \frac{10 + 7 + 13 + 20 + 15}{5}

\Rightarrow ¯ x = \frac{65}{5} = 13

अतः, 5 व्यक्तियों द्वारा एक सामाजिक कार्य करने में एक सप्ताह में लगाया गया माध्य समय 13 घंटे था।

(ii) जब बंटन अवर्गीकृत बारंबारता बंटन हो:

माध्य

¯ x =

n \sum i = 1 f_{i} x_{i}

n \sum i = 1 f_{i}

जहाँ

n \sum i = 1 f_{i} =

दिए गए आंकड़ों की बारंबारताओं का योग हैं
तथा

n \sum i = 1 f_{i} x_{i} =

दिए गए आंकड़े और उनकी बारंबारताओं के गुणनफल का योग हैं।

उदाहरण:- एक विद्यालय के 30 विद्यार्थियों द्वारा प्राप्त किए गए अंक हैं :

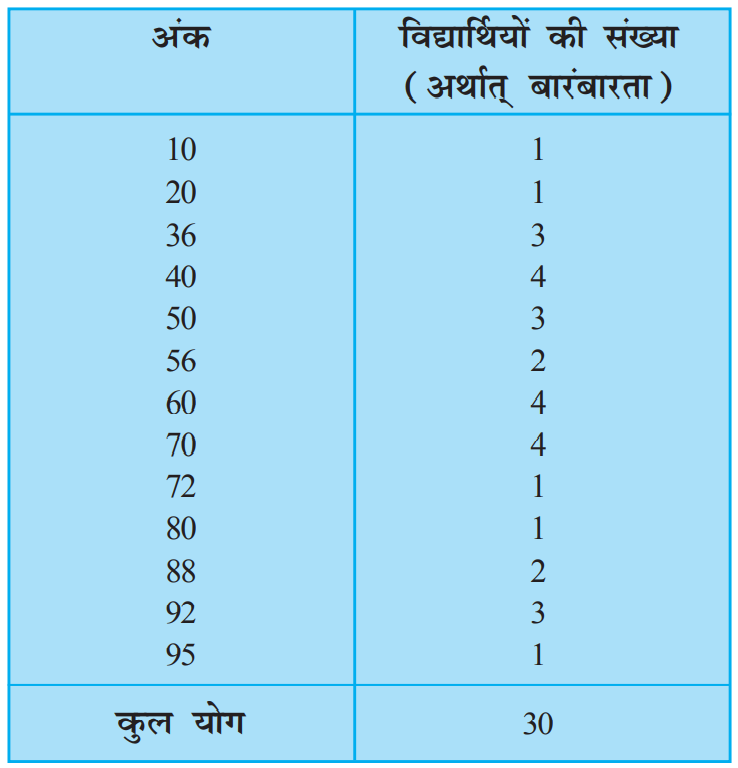
ocr_image

इन आंकड़ों का माध्य ज्ञात कीजिए।

चूंकि यहाँ आंकड़े बड़ी संख्या में दिए गए हैं तथा आंकड़ों की पुनरावृत्ति भी हो रही है इसलिए हमें पहले बारंबारता सारणी बना लेनी चाहिए फिर हम माध्य आसानी से ज्ञात कर सकते हैं, तो सारणी कुछ इस प्रकार है:

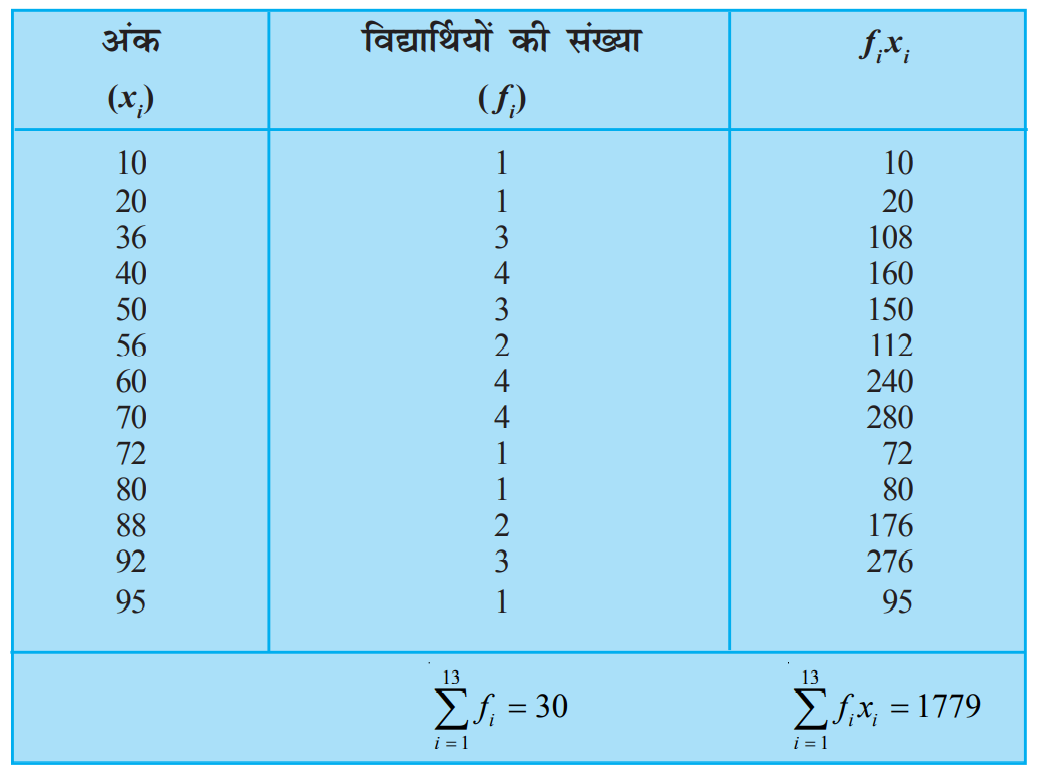
ocr_image

हम जानते हैं की, माध्य

¯ x =

n \sum i = 1 f_{i} x_{i}

n \sum i = 1 f_{i}

अतः माध्य

¯ x = \frac{1779}{30} = 59.3

माध्यक (Median) : प्रेक्षणों को आरोही या अवरोही क्रम में रखने पर प्रेक्षणों का एक ऐसा मान जो सभी प्रेक्षणों को अपने दोनों तरफ बराबर - बराबर संख्या में विभाजित करे, माध्यक कहलाता है।

माध्यक निकालने के लिए दो स्थितियाँ हैं:-
(i) जब प्रेक्षणों की संख्या $(n)$ विषम हो:

माध्यक

= \frac{n + 1}{2}

वें प्रेक्षण का मान

(ii) जब प्रेक्षणों की संख्या $(n)$ सम हो:

माध्यक

= \frac{n}{2}

वें और

(\frac{n}{2} + 1)

वें प्रेक्षणों के मानों का माध्य होता है।

अतः, माध्यक

= \frac{1}{2}

{

(\frac{n}{2})

वें प्रेक्षण का मान

+ (\frac{n}{2} + 1)

वें प्रेक्षण का मान}

3. बहुलक (Mode) : बहुलक प्रेक्षणों का वह मान होता है जो बार - बार घटित होता रहता है या हम ये भी कह सकते हैं कि जो प्रेक्षण सबसे अधिक बार आता है अर्थात जिसकी बारंबारता सबसे अधिक होती है उसे उस समूह का बहुलक कहते हैं।

जैसे - 10, 2, 7, 9, 6, 5, 9, 7, 6, 8, 6

आंकड़ों में एक जैसे अंकों को एक साथ लिखने पर,
2, 5, 6, 6, 6, 7, 7, 8, 9, 9, 10

अतः स्पष्ट हैं कि ऊपर आंकड़ों मे

6

सबसे अधिक बार (तीन बार ) आया हैं। अतः बहुलक

6

होगा।

OMR (One Minute Revision)

(i) माध्य : प्रेक्षणों के सभी मानों के योग को प्रेक्षणों की कुल संख्या से भाग देने पर माध्य प्राप्त हो जाता है। इसे $¯ x$ से प्रकट किया जाता है।
अतः माध्य $(¯ x) =$

n \sum i = 1 x_{i}

n

अवर्गीकृत बारंबारता बंटन के लिए माध्य

(¯ x) =

n \sum i = 1 f_{i} x_{i}

n \sum i = 1 f_{i}

होता है।

(ii) माध्यक : यह सबसे मध्य वाले प्रेक्षण का मान होता है।

यदि

n

विषम संख्या है, तो
माध्यक

= \frac{n + 1}{2}

वें प्रेक्षण का मान

यदि

n

सम संख्या है, तो
माध्यक

= (\frac{n}{2})

वें और

(\frac{n}{2} + 1)

वें प्रेक्षणों के मानों का माध्य होता हैं।

(iii) बहुलक : बहुलक प्रेक्षण का वह मान होता है जो बार - बार घटित होता रहता है, अर्थात अधिकतम बारंबारता वाले प्रेक्षण को बहुलक कहा जाता है।

उदाहरण 12

निम्नलिखित आंकड़ों की माध्यिका ज्ञात करे:
29, 31, 18, 41, 57, 45, 23, 35
उपर्युक्त आंकड़ों में यदि 29 को 21 से तथा 31 को 33 से प्रतिस्थापित (replace) किया जाये तो नई माध्यिका ज्ञात करे।

दिए गए आंकड़ों को आरोही क्रम में रखने पर,

18, 23, 29, 31, 35, 41, 45, 57

यहाँ प्रेक्षणो कि संख्या $n = 8$ जो कि सम संख्या है

$∴$ माध्यिका $= \frac{1}{2}$ { $\frac{n}{2}$ वें पद का मान $+ (\frac{n}{2} + 1)$ वें पद का मान }

$= \frac{1}{2}$ { $\frac{8}{2}$ वें पद का मान $+ (\frac{8}{2} + 1)$ वें पद का मान }

$= \frac{1}{2}$ { $4$ वें पद का मान $+ (4 + 1)$ वें पद का मान }

$= \frac{1}{2}$ { $4$ वें पद का मान $+ 5$ वें पद का मान }

$= \frac{1}{2} (31 + 35)$

$= \frac{1}{2} (66)$

$= 33$

चूंकि प्रश्न के अनुसार,

29 के स्थान पर 21 तथा 31 के स्थान पर 33 लिखने पर,

18, 23, 21, 33, 35, 41, 45, 57

$∴$ माध्यिका $= \frac{1}{2}$ { $\frac{n}{2}$ वें पद का मान $+ (\frac{n}{2} + 1)$ वें पद का मान }

$= \frac{1}{2}$ { $\frac{8}{2}$ वें पद का मान $+ (\frac{8}{2} + 1)$ वें पद का मान }

$= \frac{1}{2}$ { $4$ वें पद का मान $+ (4 + 1)$ वें पद का मान }

$= \frac{1}{2}$ { $4$ वें पद का मान $+ 5$ वें पद का मान }

$= \frac{1}{2} (33 + 35)$

$= \frac{1}{2} (68)$

$= 34$

अतः आंकड़े 29, 31, 18, 41, 57, 45, 23, 35 की माध्यिका 33 हैं तथा इन आंकड़ों में यदि 29 को 21 से तथा 31 को 33 से प्रतिस्थापित (replace) किया जाये तो नई माध्यिका 34 होंगी।

Learn more

उदाहरण 13

निम्नलिखित आंकड़े आरोही क्रम में व्यवस्थित किये गये हैं: 29, 32, 48, 50, $x$ , $x + 2$ , 72, 78, 84, 95
यदि आंकड़ों की माध्यिका (माध्यक) 63 हो तो $x$ का मान ज्ञात कीजिए।

दिया है;

29, 32, 48, 50, $x$ , $x + 2$ , 72, 78, 84, 95

यहाँ, प्रेक्षणों कि संख्या $n = 10$ जो कि सम संख्या है तथा माध्यिका 63 हैं।

$∴$ माध्यिका $= \frac{1}{2}$ { $\frac{n}{2}$ वें पद का मान $+ (\frac{n}{2} + 1)$ वें पद का मान }

$\Rightarrow 63 = \frac{1}{2}$ { $\frac{10}{2}$ वें पद का मान $+ (\frac{10}{2} + 1)$ वें पद का मान }

$\Rightarrow 63 = \frac{1}{2}$ { $5$ वें पद का मान $+ (5 + 1)$ वें पद का मान }

$\Rightarrow 63 = \frac{1}{2}$ { $5$ वें पद का मान $+ 6$ वें पद का मान }

$\Rightarrow 63 = \frac{1}{2} (x + x + 2)$

$\Rightarrow 63 \times 2 = 2 x + 2$

$\Rightarrow 2 x = 126 - 2$

$\Rightarrow x = \frac{124}{2} = 62$

$\Rightarrow$ अतः $x = 62$

Learn more

उदाहरण 14

यदि निम्नलिखित बारंबारता बंटन का माध्य $6$ है, तो $p$ का मान ज्ञात कीजिए।
$\begin{matrix} x : & 2 & 4 & 6 & 10 & p + 5 f : & 3 & 2 & 3 & 1 & 2 \end{matrix}$

यहाँ, $x_{i}$ प्रेक्षणों की संख्या तथा $f_{i}$ उनकी बारंबारता हैं।

हम जानते हैं की, अवर्गीकृत बारंबारता बंटन के लिए :

माध्य $¯ x =$

n \sum i = 1 f_{i} x_{i}

n \sum i = 1 f_{i}

जहाँ

n \sum i = 1 f_{i} =

दिए गए आंकड़ों की बारंबारताओं का योग हैं
तथा

n \sum i = 1 f_{i} x_{i} =

दिए गए आंकड़े और उनकी बारंबारताओं के गुणनफल का योग हैं।

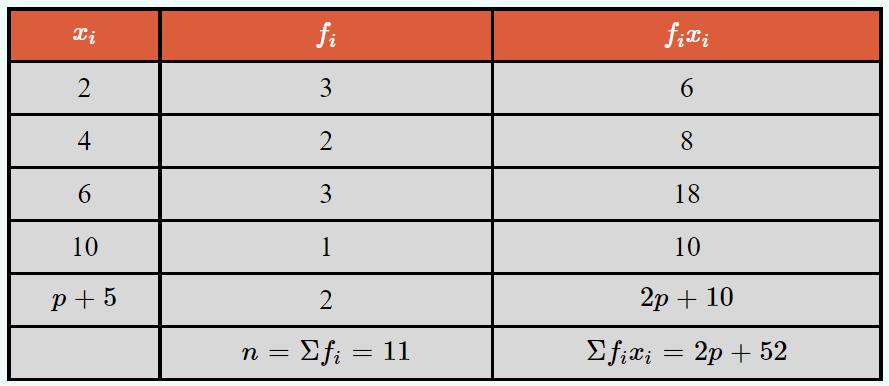
ocr_image

अतः

n = Σ f_{i} = 11

तथा

Σ f_{i} x_{i} = 2 p + 52

∴

माध्य

¯ x = \frac{2 p + 52}{11}

\Rightarrow 6 = \frac{2 p + 52}{11}

\Rightarrow 66 = 2 p + 52

\Rightarrow 2 p = 14

\Rightarrow p = 7

Learn more

उदाहरण 15

निम्न सारणी से एक फैक्ट्री के काम कर रहे 60 कर्मचारियों का माध्य वेतन ज्ञात कीजिएः

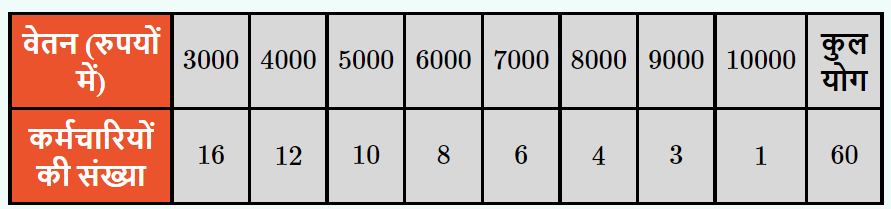
हम जानते हैं की अवर्गीकृत बारंबारता बंटन के लिए :

माध्य $¯ x =$

n \sum i = 1 f_{i} x_{i}

n \sum i = 1 f_{i}

जहाँ

n \sum i = 1 f_{i} =

दिए गए आंकड़ों की बारंबारताओं का योग हैं
तथा

n \sum i = 1 f_{i} x_{i} =

दिए गए आंकड़े और उनकी बारंबारताओं के गुणनफल का योग हैं।

यहाँ,

f_{i}

कर्मचारियों की संख्या तथा

x_{i}

वेतन (रुपयों में) हैं।

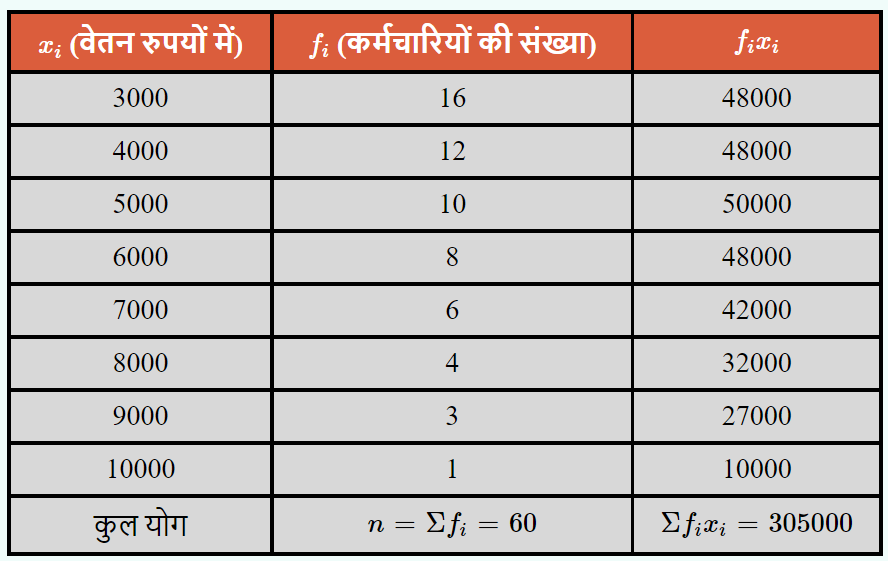
ocr_image

अतः माध्य

¯ x =

n \sum i = 1 f_{i} x_{i}

n \sum i = 1 f_{i}

= \frac{305000}{60}

= \frac{30500}{6}

= 5083.33

रुo

Learn more

सारांश

इस अध्याय में, हमने निम्नलिखित बिंदुओं का अध्ययन किया है:

एक निश्चित उद्देश्य से एकत्रित किए गए तथ्यों या अंकों को आंकड़े कहा जाता है।

सांख्यिकी वह विज्ञान है जिसमें किसी क्षेत्र से संबंधित आंकड़े जो विभिन्न कारणों से प्रभावित होते हैं; का संकलन, वर्गीकरण, सारणीकरण, प्रस्तुतीकण, विश्लेषण, निर्वचन (Interpretation) तथा पूर्वानुमान किया जाता है जिससे निर्धारित उद्देश्य की पूर्ति हो सके।

किस प्रकार आंकड़ों को आलेखों, आयतचित्रों तथा बारंबारता बहुभुजों द्वारा आलेखीय रूप में प्रस्तुत किया जा सकता है।

अवर्गीकृत आंकड़ों की केन्द्रीय प्रवृत्ति के तीन माप हैं:

(i) माध्य : प्रेक्षणों के सभी मानों के योग को प्रेक्षणों की कुल संख्या से भाग देने पर यह प्राप्त हो जाता है। इसे

¯ x

से प्रकट किया जाता है।
अतः माध्य

(¯ x) =

n \sum i = 1 x_{i}

n

हैं।

अवर्गीकृत बारंबारता बंटन के लिए यह

¯ x =

n \sum i = 1 f_{i} x_{i}

n \sum i = 1 f_{i}

होता है।

(ii) माध्यक : यह सबसे मध्य वाले प्रेक्षण का मान होता है।

यदि

n

विषम संख्या है, तो माध्यक

= \frac{n + 1}{2}

वें प्रेक्षण का मान

यदि

n

सम संख्या है, तो माध्यक

= (\frac{n}{2})

वें और

(\frac{n}{2} + 1)

Home
Ask Doubt
Profile