पृष्ठीय क्षेत्रफल और आयतन कक्षा 9 गणित
भूमिका
पिछला अध्याय में हमने कुछ समतल आकृति (त्रिभुज, चतुर्भुज) का क्षेत्रफल निकालने के बारे में पढ़ा है तथा हमने यह भी पढ़ा है, की समतल में बनी आकृति द्विविमीय आकृति कहलाती है। द्विविमीय आकृति में दो विमा (dimension) (लम्बाई और चौड़ाई) होती है। अब इस अध्याय मे हम त्रिविमीय आकृति का अध्ययन करेंगे जिनमें तीन विमाये (लम्बाई, चौड़ाई और ऊँचाई) होती हैं। तीन विमाओं वाली आकृति को ठोस (solid) कहते हैं। यहाँ हम ठोस आकृतियों घनाभ, घन, बेलन, शंकु और गोले के आयतन एवं पृष्ठीय क्षेत्रफल का अध्ययन करेंगे।
आइये जानते है, पृष्ठीय क्षेत्रफल और आयतन को और करीब से...
आकृति: दो प्रकार की होती हैं।
(1) समतल आकृति
(2) ठोस आकृति
समतल आकृति: ऐसी आकृति जिन्हें हम अपनी अभ्यासपुस्तिका (Note Book) पर खींच सकते हैं। समतल आकृति (Plane Figure) कहलाती हैं तथा समतल आकृति में दो विमा (Dimension), लंबाई और चौड़ाई होती हैं, इसलिए इन्हे द्विविमीय आकृति भी कहते हैं।
जैसे -

ठोस आकृति: हमें दैनिक जीवन में अनेक ठोस, जैसे ईंट, बक्सा, माचिस की डिबिया, कमरा, प्लेट, जग, डस्टर आदि देखने को मिलते हैं। इन आकृतियों में लम्बाई, चौड़ाई तथा ऊँचाई होती हैं, इसलिए इन्हें त्रिविमीय (three dimensional) आकृति कहते हैं। तीन विमाओं वाली आकृति को घनाकृति या ठोस (solid) भी कहते हैं।
जैसे -
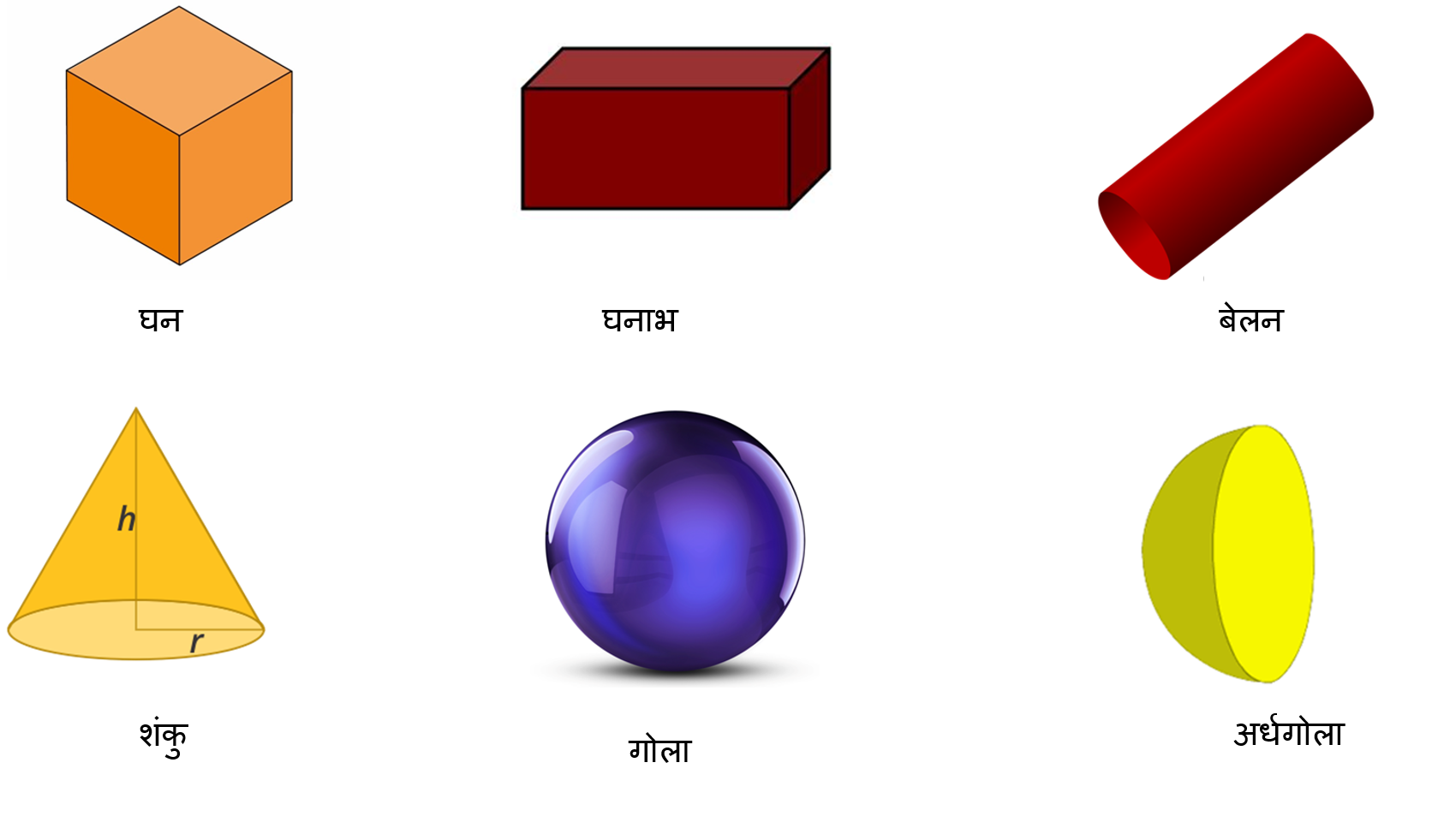
पृष्ठीय क्षेत्रफल
किसी त्रिविमीय या ठोस वस्तु की सतह का कुल क्षेत्रफल उसका पृष्ठीय क्षेत्रफल कहलाता है।
जैसे की एक घनाभ लेते हैं, चूंकि घनाभ में छः फलक होते हैं।

यदि इस घनाभ को बनाने के लिए कागज का उपयोग किया जाए, तो जितना कागज लगेगा, वही घनाभ का पृष्ठीय क्षेत्रफल होगा या इसको बाहर से पेंट करने मे जितना पेंट लगेगा, इसका पृष्ठीय क्षेत्रफल होगा।
अतः पृष्ठीय क्षेत्रफल = फलक 1 का क्षेत्रफल + फलक 2 का क्षेत्रफल + फलक 3 का क्षेत्रफल + फलक 4 का क्षेत्रफल + फलक 5 का क्षेत्रफल + फलक 6 का क्षेत्रफल
आयतन
किसी त्रिविमीय या ठोस वस्तु द्वारा घिरी हुई जगह उसका आयतन कहलाता है।
जैसे की गेंद, डस्टर, पुस्तक ये सभी चीजे अपना एक स्थान घेरती हैं और ये जितना स्थान घेरती हैं उसको, इसका आयतन कहते हैं।
जैसे - किसी बाल्टी में जीतना पानी आ सकता हैं, वही उस बाल्टी का आयतन होगा।
घनाभ और घन का पृष्ठीय क्षेत्रफल
घनाभ (Cuboid)
छः आयताकार पृष्ठों से घिरे आकृति को घनाभ कहते हैं।जैसै - दियासलाई की डिबिया, ईंट, बक्सा आदि।
घनाभ के आमने-सामने के पृष्ठ (फलक) बराबर तथा समांतर होते हैं। घनाभ में 12 किनारे (कोर) तथा 8 कोने होते हैं। इन कोनों को शीर्ष कहते हैं। विपरीत शीर्षों (opposite vertices) को मिलाने वाली रेखा घनाभ का विकर्ण कहलाता है। घनाभ में कुल चार विकर्ण होते हैं जिनकी लम्बाई बराबर होती हैं।
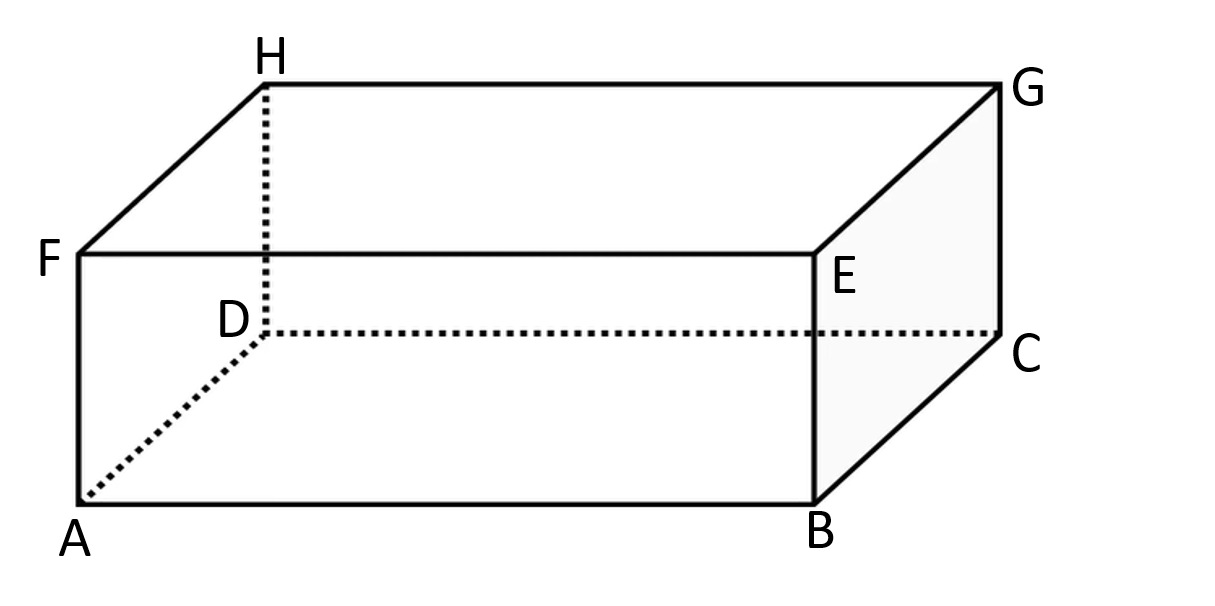
अतः चित्र में देख सकते हैं की, एक घनाभ है जिसमें AB लम्बाई, BC चौड़ाई तथा EB ऊँचाई है। आमने-सामने के पृष्ठ ABCD, FEGH बराबर तथा समान्तर हैं। इसी प्रकार AFHD, BEGC बराबर और समान्तर है एवं पृष्ठ ABEF तथा DCGH भी बराबर और समान्तर हैं। BH, AG, CF तथा DE घनाभ के विकर्ण हैं।
घनाभ का पृष्ठीय क्षेत्रफल
माना कि घनाभ की लम्बाई =l, चौड़ाई =b तथा ऊँचाई =h हैं।
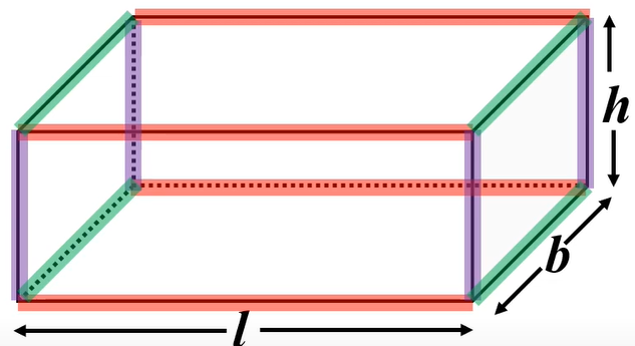
चूंकि घनाभ के फलक आयताकार होते हैं।

घनाभ का कुल क्षेत्रफल, छः आयताकार फलकों के क्षेत्रफल का योग होगा।
फलक I का क्षेत्रफल =l×b
फलक II का क्षेत्रफल =l×b
फलक III का क्षेत्रफल =l×h
फलक IV का क्षेत्रफल =l×h
फलक IV का क्षेत्रफल =b×h
फलक V का क्षेत्रफल =b×h
घनाभ का कुल क्षेत्रफल = फलक I का क्षेत्रफल + फलक II का क्षेत्रफल + फलक III का क्षेत्रफल
+ फलक IV का क्षेत्रफल + फलक V का क्षेत्रफल + फलक VI का क्षेत्रफल
=l×b+l×b+l×h+l×h+b×h+b×h
=2(l×b)+2(l×h)+2(b×h)
अतः घनाभ का कुल पृष्ठीय क्षेत्रफल =2(l×b+l×h+b×h)
घन (Cube)
घन एक ऐसी त्रिविमीय आकृति को कहा जाता है जिसकी लम्बाई, चौड़ाई एवं ऊँचाई सामान होती हैं। एक घन में 6 फलक, 12 किनारे एवं 8 कोने होते हैं।
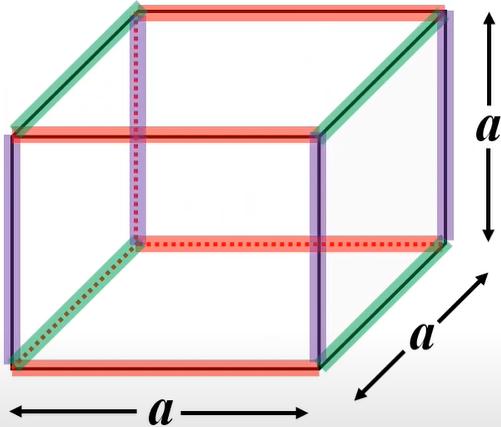
जैसे - पासा, रुबिक्स क्यूब (rubik's cube)।

घन के सभी फलक वर्गाकार होते हैं क्योंकि इसके सभी भुजाओं (किनारों) की लम्बाई समान होती है। वास्तव में घनाभ जिसकी लम्बाई, चौड़ाई और ऊँचाई बराबर हों एक घन (cube) कहलाता है।
लंबाई = चौड़ाई = ऊँचाई
l=b=h=a
घन का पृष्ठीय क्षेत्रफल
हम जानते हैं की,
घनाभ का कुल पृष्ठीय क्षेत्रफल =2(l×b+l×h+b×h)
∴घन का कुल पृष्ठीय क्षेत्रफल =2(a×a+a×a+a×a)
=2(a2+a2+a2)
=2(3a2)
अतः घन का कुल पृष्ठीय क्षेत्रफल =6a2
पार्श्व पृष्ठीय क्षेत्रफल (Lateral surface area)
मान लीजिए हम घनाभ और घन के छः फलकों (faces) में से केवल चार फलकों के क्षेत्रफल, निचले और ऊपरी फलकों को छोड़कर (फलक I और II को छोड़कर) ज्ञात करें। ऐसी स्थिति में, इन चारों फलकों का क्षेत्रफल पार्श्व पृष्ठीय क्षेत्रफल कहलाता है।
जैसे की अगर हम एक कमरे को देखे, तो अगर फर्श को और छत को छोड़कर बाकी के चारों दीवारों आगे, पीछे, दाएं और बाएं का क्षेत्रफल मिलाकर पार्श्व पृष्ठीय क्षेत्रफल हैं।
घनाभ का पार्श्व पृष्ठीय क्षेत्रफल = फलक III का क्षेत्रफल + फलक IV का क्षेत्रफल + फलक V का क्षेत्रफल + फलक VI का क्षेत्रफल
=l×h+l×h+b×h+b×h
=2(l×h+b×h)
घनाभ का पार्श्व पृष्ठीय क्षेत्रफल =2h(l+b)
इसी प्रकार, घन का पार्श्व पृष्ठीय क्षेत्रफल
चूंकि घन में, लंबाई = चौड़ाई = ऊँचाई
अतः घन का पार्श्व पृष्ठीय क्षेत्रफल =2a(a+a)
=2a(2a)
घन का पार्श्व पृष्ठीय क्षेत्रफल =4a2
Note : क्षेत्रफल का मात्रक (unit) वर्ग इकाई (वर्ग मात्रक) होता है।
OMR (One Minute Revision)
| आकृति | सम्पूर्ण पृष्ठीय क्षेत्रफल (वर्ग इकाई) | पार्श्व पृष्ठीय क्षेत्रफल (वर्ग इकाई) | |
|---|---|---|---|
| घनाभ | 2(l×b+l×h+b×h) | 2h(l+b) | l= लंबाई b= चौड़ाई h= ऊँचाई |
| घन | 6a2 | 4a2 | a= घन का किनारा |
उदाहरण 1
एक चौक का डिब्बा जिसकी लंबाई, चौड़ाई और ऊंचाई क्रमशः 16 सेंटीमीटर, 8 सेंटीमीटर और 6 सेंटीमीटर है इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
चौक का डिब्बा एक घनाभ के आकार का होता है।
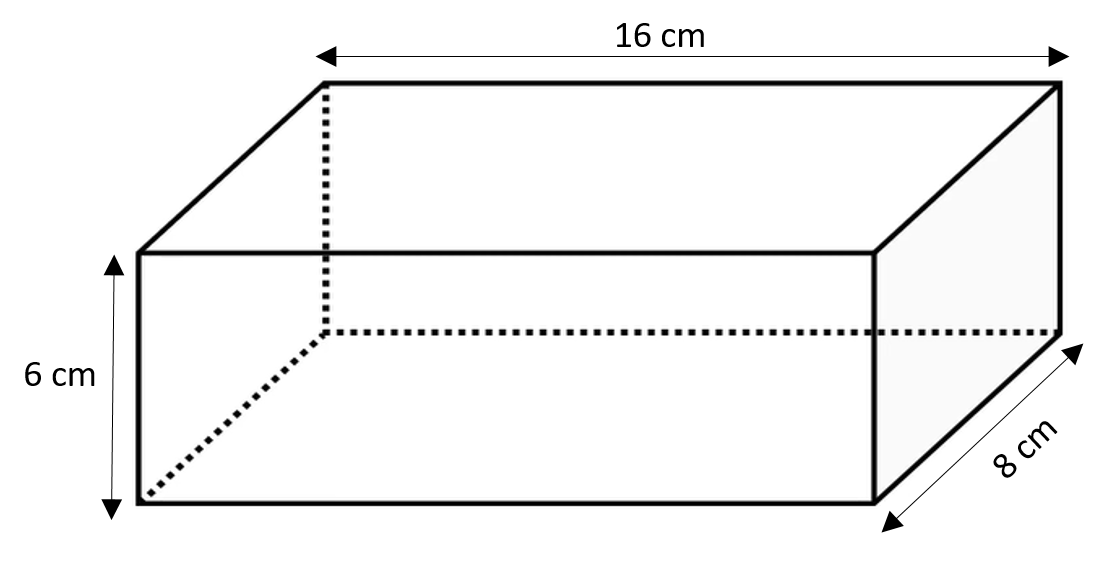
यहाँ, लंबाई l=16 सेमी, चौड़ाई b=8 सेमी तथा ऊँचाई h=6 सेमी
∴ घनाभ का पृष्ठीय क्षेत्रफल =2(lb+bh+lh)
=2(16×8+8×6+16×6) सेमी 2
=2(128+48+96) सेमी 2
=544 सेमी 2
अतः घनाभ का पृष्ठीय क्षेत्रफल 544 सेमी 2 हैं।
उदाहरण 2
मैरी अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक घनाभाकार बॉक्स पर रखना चाहती है, जिसे सांता क्लॉज के चित्र के साथ एक रंगीन कागज से ढका जाना है ( देखिए आकृति )। उसका यह जानना आवश्यक है कि उसे कितना कागज खरीदना चाहिए। यदि उपरोक्त बॉक्स की लम्बाई, चौड़ाई, और ऊँचाई क्रमश: 80 cm, 40 cm और 20 cm है, तो उसे 40 cm भुजा वाली कागज की कितनी वर्गाकार शीटों की आवश्यकता होगी?
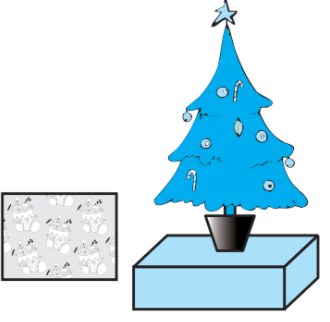
चूँकि मैरी बॉक्स के ऊपरी पृष्ठ को कागज से ढकना चाहती है, इसलिए इस कार्य के लिए आवश्यक कागज इस बॉक्स के पृष्ठीय क्षेत्रफल के बराबर होगा, जो एक घनाभ के आकार का है।
प्रश्न से, बॉक्स की लंबाई l=80 cm, चौड़ाई b=40 cm और ऊँचाई h=20 cm
अतः बॉक्स का पृष्ठीय क्षेत्रफल =2(lb+bh+hl)
=2[(80×40)+(40×20)+(20×80)]cm2
=2[3200+800+1600]cm2
=2×5600cm2
=11200cm2
अब, प्रत्येक शीट का क्षेत्रफल =40×40=1600cm2
∴ आवश्यक वर्गाकार शीटों की संख्या =
=11200cm21600cm2=7
अतः मैरी को कागज की 7 शीटों की आवश्यकता है।
उदाहरण 3
एक घनाकार डिब्बे का एक किनारा 10 cm लंबाई का है तथा एक अन्य घनाभाकार डिब्बे की लंबाई, चौड़ाई और ऊँचाई क्रमश: 12.5 cm, 10 cm और 8 cm है।
(i) किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है और कितना अधिक है ?
(ii) किस डिब्बे का कुल पृष्ठीय क्षेत्रफल कम है और कितना कम है ?
(i) घनाकार डिब्बे की लंबाई =10 cm है।
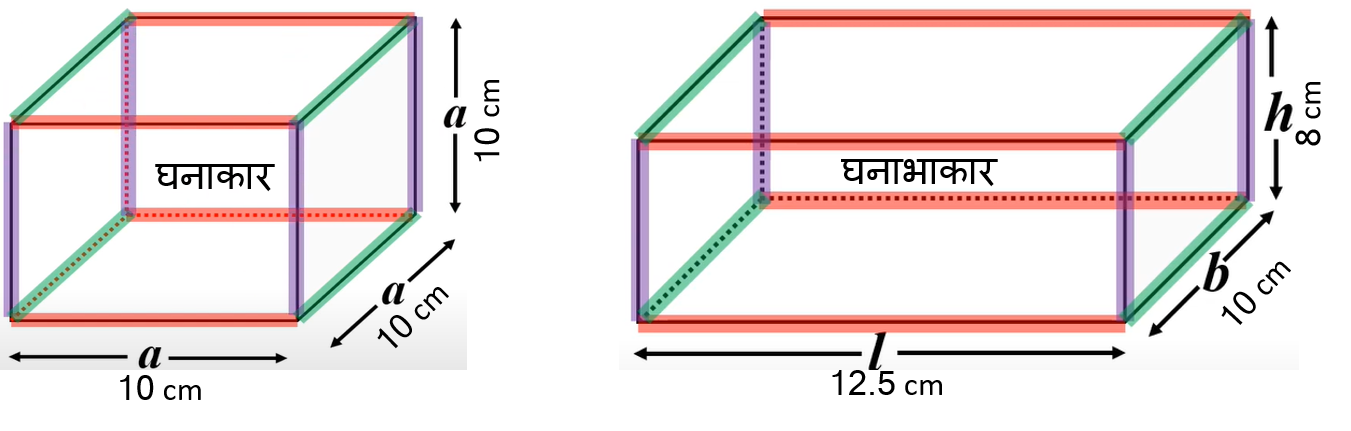
घनाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल =4a2
=4(10)2 cm2
=4(100) cm2
=400 cm2
घनाभाकार डिब्बे की लंबाई l= 12.5 cm, चौड़ाई b= 10 cm और ऊँचाई h= 8 cm है।
घनाभाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल =2(l+b)h
=2(12.5+10)×8cm2
=2(22.5)×8cm2
=360cm2
पार्श्व पृष्ठीय क्षेत्रफलों में अंतर =400cm2−360cm2
=40cm2
अतः, घनाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल घनाभाकार डिब्बे के पार्श्व पृष्ठीय क्षेत्रफल से 40cm2 अधिक है।
(ii) घनाकार डिब्बे की लंबाई 10 cm है।
घनाकार डिब्बे का कुल पृष्ठीय क्षेत्रफल =6a2
=6(10)2cm2
=6(100)cm2
=600cm2
घनाभाकार डिब्बे का कुल पृष्ठीय क्षेत्रफल =2(lb+bh+hl)
=2(12.5×10+10×8+8×12.5) cm2
=2(125+80+100) cm2
=2(305) cm2
=610 cm2
कुल पृष्ठीय क्षेत्रफलों में अंतर =610 cm2−600 cm2 =10 cm2
अतः, घनाकार डिब्बे का कुल पृष्ठीय क्षेत्रफल घनाभाकार डिब्बे के कुल पृष्ठीय क्षेत्रफल से 10 cm2 कम है।
एक लंब वृत्तीय बेलन का पृष्ठीय क्षेत्रफल
यदि आयत की एक भुजा स्थिर हो और आयत इस स्थिर भुजा के चारों ओर घूमे तो घूमने से जो पिण्ड बनता है उसे लंब वृत्तीय बेलन (right circular cylinder) कहते हैं या जब कोई रेखा किसी वृत्त की परिधि पर इस प्रकार घूमे कि वह वृत्त के तल पर हमेशा लंब रहे तो घूमने से जो पिण्ड बनता है उसे लंब वृत्तीय बेलन कहते हैं।
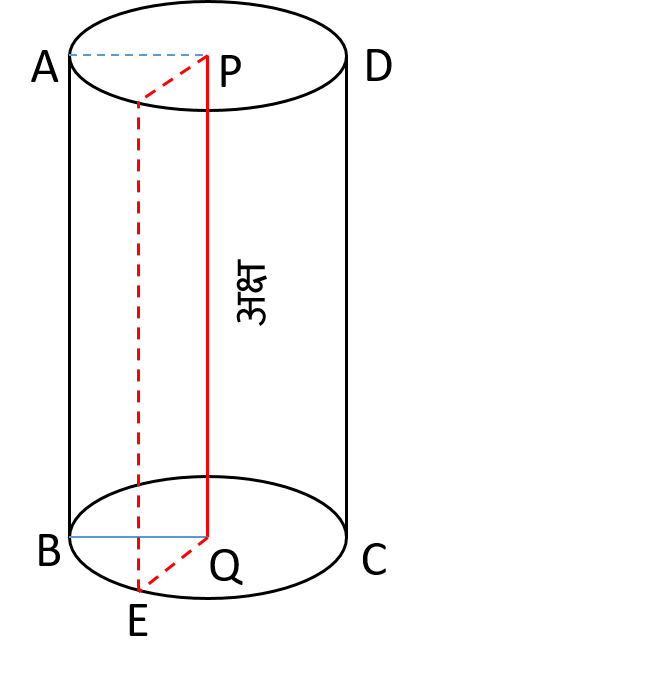
चित्र में रेखा AB के वृत्त BEC की परिधि पर घूमने से लम्ब वृत्तीय बेलन बनता है। घूमने वाली रेखा AB जनक रेखा (generating line) तथा केन्द्रों को मिलाने वाली रेखा PQ बेलन का अक्ष है। वृत्त BEC बेलन का आधार है।
यदि कागज के बहुत सारे वृत्ताकार शीटों को एक के ऊपर एक आधार के लम्बवत h ऊँचाई तक रखा जाय तो, इस तरह से प्राप्त ठोस (पिंड) एक लम्ब वृत्तीय बेलन होगा। वृत्त की त्रिज्या बेलन की त्रिज्या कहलाती है तथा यदि वृत्ताकार शीटों को h ऊँचाई तक रखा गया है तो बेलन की ऊँचाई h होगा।
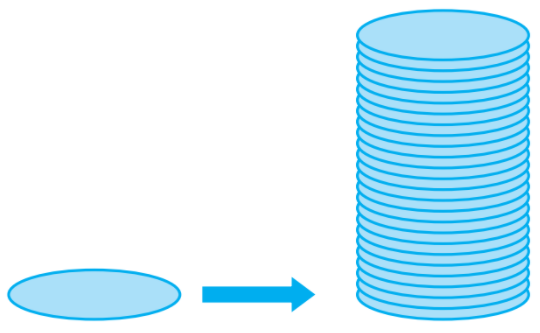
लंब वृत्तीय बेलन का आधार तथा ऊपरी सतह वृत्ताकार होता है। यदि इस वृत्त की त्रिज्या r हो तो दोनों वृत्ताकार सतहों का क्षेत्रफल (πr2+πr2) 2πr2 होगा।
बेलन का वक्र पृष्ठीय क्षेत्रफल
बेलन का वक्र पृष्ठ जानने के लिए एक खोखला बेलन लेते हैं और अक्ष के समान्तर इसे काटकर जमीन पर फैला दिया तो पूरा पृष्ठ एक आयत के रूप में बदल गया जिसकी लम्बाई बेलन के आधार की परिधि होगी तथा चौड़ाई बेलन की ऊँचाई होगी।
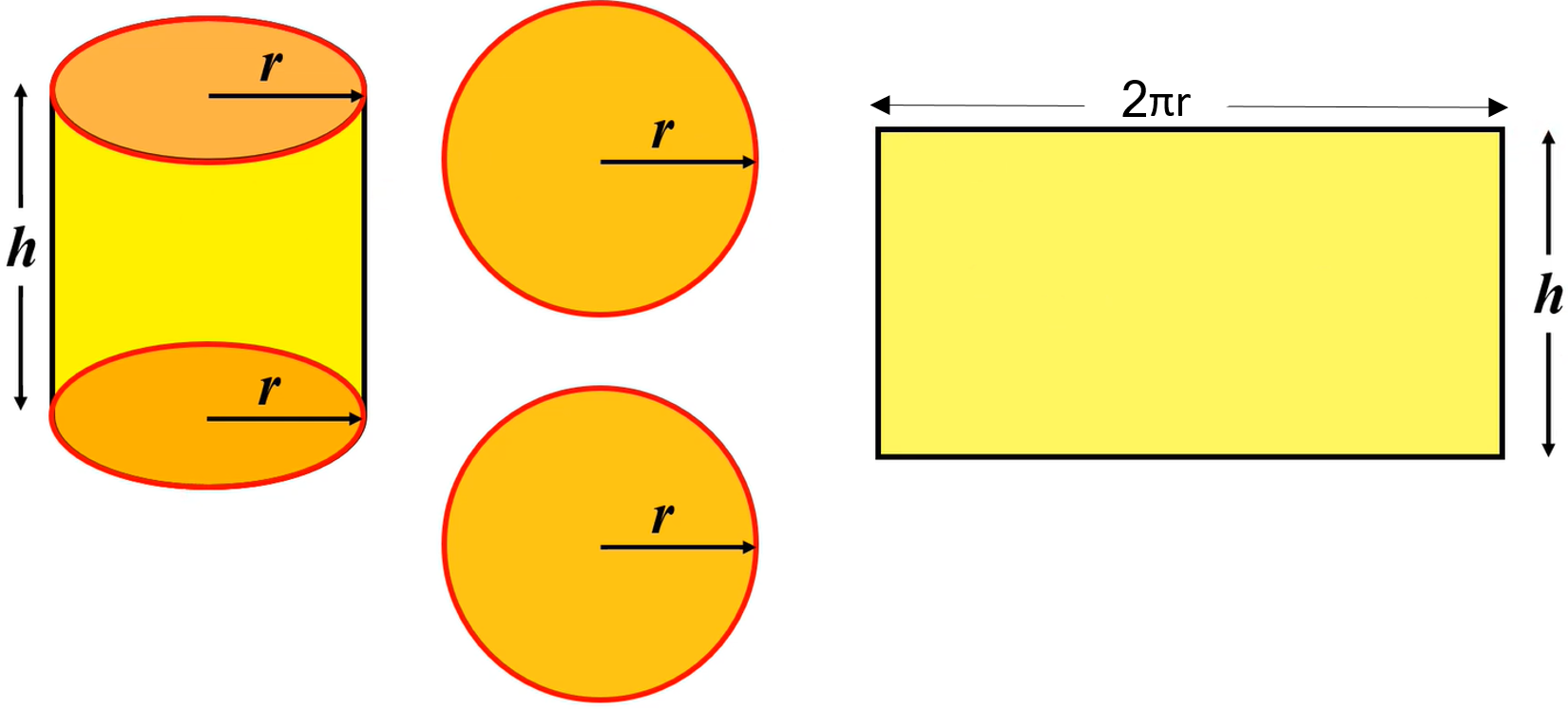
बेलन का वक्र पृष्ठीय क्षेत्रफल = आधार की परिमाप × ऊँचाई
चूंकि यहाँ आधार वृत्ताकार हैं और हम जानते हैं की वृत्त का परिमाप 2πr होता हैं।
∴ बेलन का वक्र पृष्ठीय क्षेत्रफल =2πr×h
अतः बेलन का वक्र पृष्ठीय क्षेत्रफल =2πrh
जहाँ r बेलन की त्रिज्या और h ऊँचाई है।
बेलन का कुल पृष्ठीय क्षेत्रफल
हम कागज का एक आयताकार शीट लेते हैं जिसकी लंबाई l तथा ऊँचाई h है यदि हम इस कागज को l की दिशा में गोल - गोल मोड़े तो हमे h ऊँचाई का एक बेलन प्राप्त होता हैं।
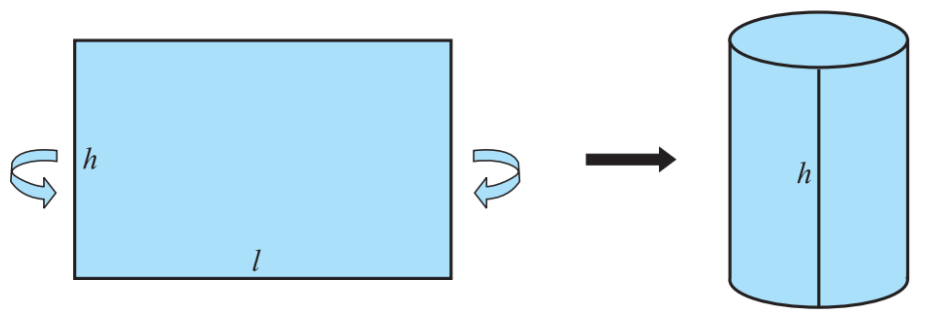
यदि बेलन के ऊपरी और निचले सिरों को भी कागज से ढकना हो, तो 2 वृत्तों ( वृत्ताकार क्षेत्रों ) की आवश्यकता होगी, जिनमे से प्रत्येक की त्रिज्या r और क्षेत्रफल πr2 होगा।
अतः बेलन का कुल पृष्ठीय क्षेत्रफल
= बेलन के दोनों आधारों का क्षेत्रफल + बेलन का वक्रपृष्ठ का क्षेत्रफल
=(πr2+πr2)+2πr×h
=(2πr2)+2πrh
=2πr(r+h)
अतः बेलन का कुल पृष्ठीय क्षेत्रफल =2πr(r+h)
OMR (One Minute Revision)
| आकृति | वक्र पृष्ठीय क्षेत्रफल (वर्ग इकाई) | सम्पूर्ण पृष्ठीय क्षेत्रफल (वर्ग इकाई) | |
|---|---|---|---|
| बेलन | 2πrh | 2πr(r+h) | r= बेलन के आधार की त्रिज्या h= ऊँचाई |
उदाहरण 4
सावित्री को अपने विज्ञान के प्रोजेक्ट के लिए एक बेलनाकार केलिडोस्कोप (kaleidoscope) का मॉडल बनाना था। वह इस केलिडोस्कोप की वक्र बनाने के लिए चार्ट कागज (chart paper) का प्रयोग करना चाहती थी (देखिए आकृति में)। यदि वह 25 सेमी लम्बाई और 3.5 सेमी त्रिज्या का केलिडोस्कोप बनाना चाहती है, तो उसे चार्ट कागज के कितने क्षेत्रफल की आवश्यकता होगी (π=227 लीजिये)

बेलनाकार केलिडोस्कोप की त्रिज्या (r)=3.5 cm
केलिडोस्कोप की ऊँचाई (लंबाई) (h)=25 cm
अतः, आवश्यक चार्ट कागज़ का क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
=2×227×3.5×25
=550 cm2
अतः केलिडोस्कोप बनाने के लिए आवश्यक चार्ट कागज़ का क्षेत्रफल =550 cm2
उदाहरण 5
एक ठोस बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल 462 सेमी 2 है इसका वक्र पृष्ठीय क्षेत्रफल सम्पूर्ण पृष्ठीय क्षेत्रफल का 13 भाग है। बेलन की ऊंचाई ज्ञात कीजिए।
दिया है,
बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल =462 सेमी 2
प्रश्न के अनुसार,
वक्र पृष्ठीय क्षेत्रफल =13× सम्पूर्ण पृष्ठीय क्षेत्रफल
2πrh=13×2πr(r+h)
⇒ cancel (2pir) h = (1)/(3) xx cancel (2pir)(r +h)
⇒ h=13×(r+h)
⇒ h×3=(r+h)
⇒ 3h=(r+h)
⇒ 3h=r+h
⇒ 3h−h=r
⇒ 2h=r ..................समीकरण (i)
चूंकि सम्पूर्ण पृष्ठीय क्षेत्रफल =462 सेमी 2
∴ वक्र पृष्ठीय क्षेत्रफल =13× सम्पूर्ण पृष्ठीय क्षेत्रफल
⇒ वक्र पृष्ठीय क्षेत्रफल =13×462
⇒ वक्र पृष्ठीय क्षेत्रफल =154 सेमी 2
⇒2πrh=154
⇒2×227rh=154
⇒2h×227r=154
समीकरण (i) से, 2h=r
∴2h×227×2h=154
⇒2h2×227×2=154
⇒h2=154×72×22×2
⇒h2=494
वर्गमूल लेने पर,
h=√494
⇒h=√7×72×2
⇒h=72
⇒h=3.5 सेमी
अतः बेलन की ऊँचाई 3.5 सेमी हैं।
एक लंब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल
समकोण त्रिभुज बनाने वाली भुजाओं में से एक को स्थिर रखकर उसके चारों तरफ घुमाने से जो पिण्ड बनता है उसे लम्ब वृत्तीय शंकु (right circular cone) कहते हैं।
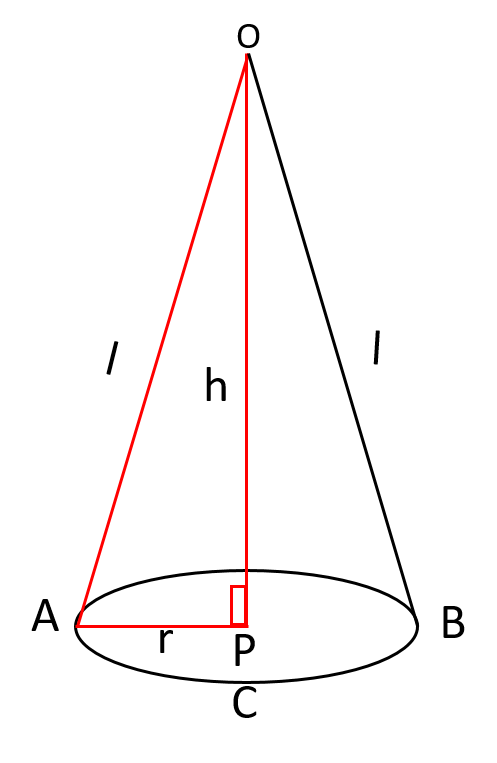
चित्र में समकोण ΔOPA अपने स्थिर भुजा OP के चारों ओर घूमकर शंकु (OACB) बनाता है।
यहाँ ACB वृत्त हैं जो शंकु का आधार हैं और O शंकु का शीर्ष हैं। शीर्ष O से वृत्त के तल पर खींचा गया लम्ब OP शंकु का ऊँचाई कहलाता हैं। शीर्ष को वृत्त पर स्थित किसी बिन्दु से मिलाने वाली रेखाखण्ड को शंकु की तिरछी ऊँचाई कहते हैं। अतः OA तथा OB शंकु की तिरछी ऊँचाई हैं। ∠AOB को शंकु का शीर्षकोण है।
जैसे - तेल डालने वाले टीप, जोकर की टोपी, आइसक्रीम कोण ये सभी वृत्तीय शंकु के उदाहरण हैं।
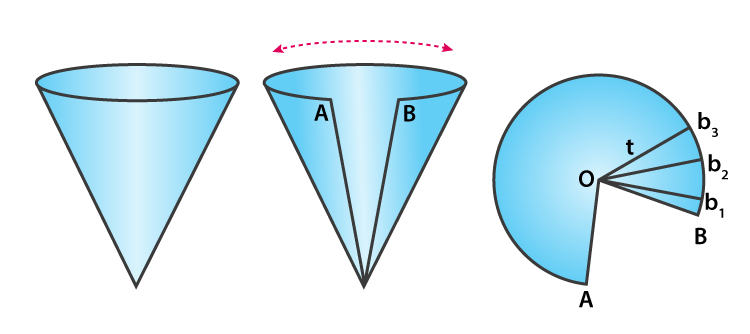
चूंकि त्रिभुज का क्षेत्रफल =12× प्रत्येक त्रिभुज का आधार ×l
शंकु का वक्र पृष्ठीय क्षेत्रफल (CSA) छोटे त्रिभुजों के क्षेत्रफलों का योग होगा
12×(b1+b2.……..bn)×l
यहाँ (b1+b2...bn) आधार की परिधि के बराबर है।
∴(b1+b2...bn)=2πr
शंकु का वक्र पृष्ठीय क्षेत्रफल =12×l×2πr=πrl
जहाँ r आधार की त्रिज्या और l तिर्यक ऊँचाई हैं।
चित्र से स्पष्ट है कि l2=r2+h2 (पाइथागोरस प्रमेय से)
जहाँ h शंकु की ऊँचाई है।
अतः l=√r2+h2
अब यदि शंकु के आधार को बंद रखना है, तो ढकने के लिए त्रिज्या वाले एक वृत्ताकार कागज के टुकड़े की आवश्यकता और होगी। इसका क्षेत्रफल πr2 होगा।
∴ शंकु का कुल पृष्ठीय क्षेत्रफल = वक्र पृष्ठ का क्षेत्रफल + वृत्ताकार आधार का क्षेत्रफल
=πrl+πr2
=πr(l+r)
अतः शंकु का कुल पृष्ठीय क्षेत्रफल =πr(l+r)
जहाँ r आधार की त्रिज्या और l तिर्यक ऊँचाई हैं।
OMR (One Minute Revision)
| आकृति | वक्र पृष्ठीय क्षेत्रफल (वर्ग इकाई) | सम्पूर्ण पृष्ठीय क्षेत्रफल (वर्ग इकाई) | |
|---|---|---|---|
| शंकु | πrl | πr(l+r) | r= शंकु के आधार की त्रिज्या l= तिर्यक ऊँचाई |
उदाहरण 6
शंकु के आकार का एक तंबू 10 मीटर ऊँचा है और उसके आधार की त्रिज्या 24 मीटर है ज्ञात कीजिए:
(i) तंबू की तिर्यक ऊँचाई
(ii) तंबू में लगे केनवास (Canvas) की लागत, यदि 1 मीटर 2 केनवास की लागत 70 रुपए है।
(i) शंकु की त्रिज्या r=24 m और ऊँचाई h=10 m है।

माना, तिर्यक ऊँचाई = l m
हम जानते हैं कि, l2=r2+h2
⇒l2=242+102
⇒l2=576+100=676
⇒l=√676=26 m
अतः, तंबू की तिर्यक ऊँचाई 26 m हैं।
(ii) तंबू में लगे केनवास का क्षेत्रफल =πrl
=227×24×26m2
चूंकि 1m2 केनवास की लागत = ₹70
∴227×24×26m2 केनवास की लागत =₹70×227×24×26m2= ₹137280
अतः, तंबू में लगे केनवास की लागत ₹137280 है।
उदाहरण 7
यदि एक शंकु की तिर्यक ऊँचाई 21 मी और आधार का व्यास 24 मी हो, तो उसका सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात करो।
दिया है,
तिर्यक ऊँचाई l= 21 मी तथा व्यास =24 मी
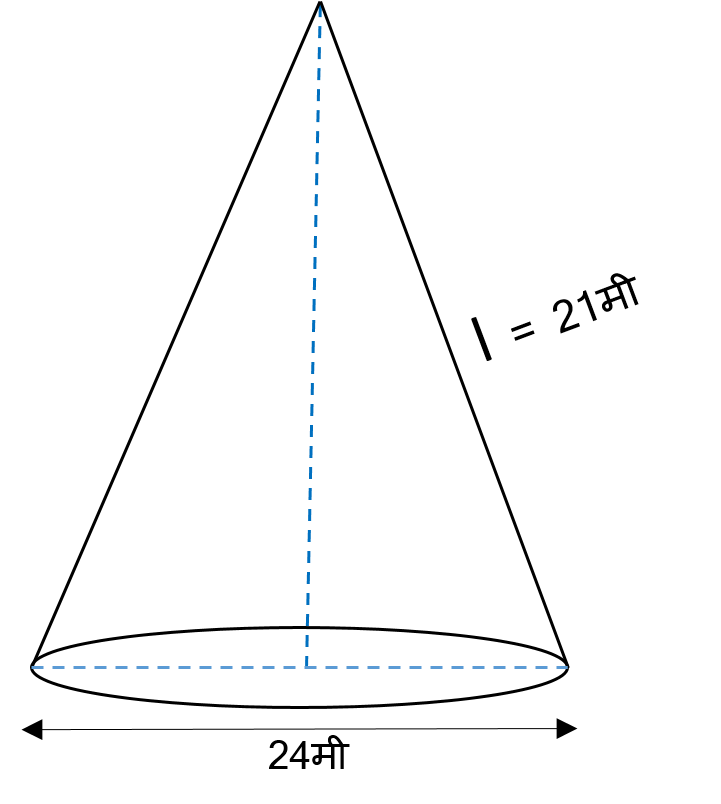
चूंकि व्यास =2×त्रिज्या
∴ त्रिज्या =
⇒ त्रिज्या r=242=12 मी
सम्पूर्ण पृष्ठीय क्षेत्रफल =πr(l+r)
=227×12(12+21) मी 2
=227×12×33 मी 2
=1244.571 मी 2
अतः शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल 1244.571 मी 2 हैं।
गोले का पृष्ठीय क्षेत्रफल
गोला (Sphere)
गोला एक ऐसी त्रिविमीय (3D) आकृति होती है, जिसमें सतह का प्रत्येक बिन्दु एक स्थिर बिन्दु से समान दूरी पर होता है तो यह आकृति गोला कहलाता है। स्थिर बिन्दु को गोले का केंद्र तथा स्थिर बिन्दु से गोले की सतह तक की दूरी, गोले की त्रिज्या कहलाती है।
उदाहरण - फुटबॉल, बॉलीबॉल, क्रिकेट बॉल आदि।
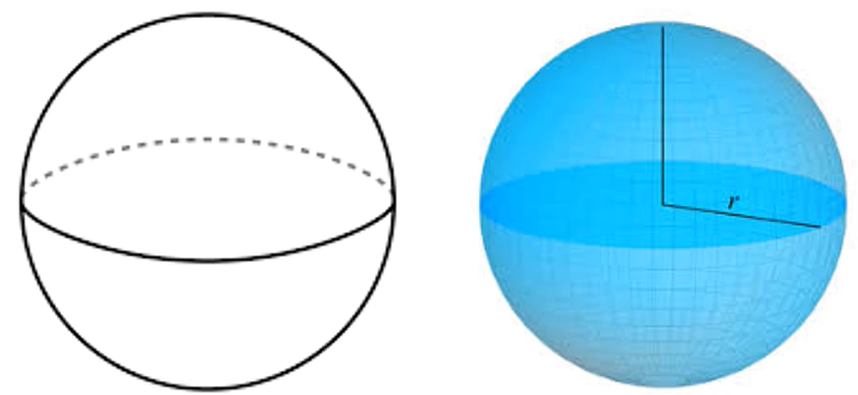
गोले का पृष्ठीय क्षेत्रफल =4πr2
जहाँ r गोले की त्रिज्या हैं।
Note: गोले के पृष्ठ पर केवल एक फलक होता है जो वक्रीय है।
अर्धगोला (Hemisphere)
एक ठोस गोला को बीच से इसके केंद्र से जाते हुए एक तल द्वारा दो भागों में काटने पर यह गोला दो बराबर भागों में विभाजित हो जाता है। प्रत्येक आधा भाग अर्धगोला (hemisphere) कहलाता है।
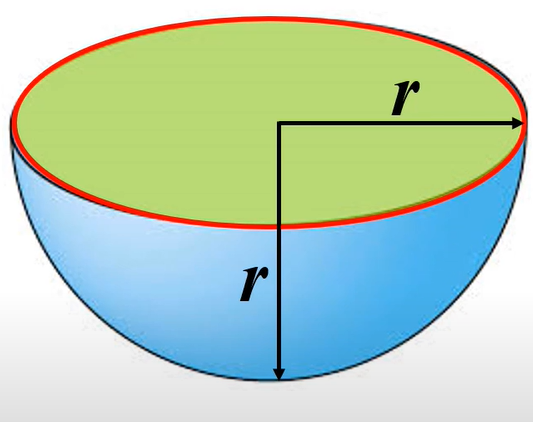
अर्घगोले में दो फलक होते हैं-
(I) वक्रीय फलक (II) समतल फलक
अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल(Curved Surface Area of Hemisphere)
अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल गोले के पृष्ठीय क्षेत्रफल का आधा होगा।
∴ अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल =12× गोले का पृष्ठीय क्षेत्रफल
=12×4πr2
=2πr2
अतः अर्द्धगोले का वक्र पृष्ठीय का क्षेत्रफल =2πr2
अर्धगोले का कुल पृष्ठीय का क्षेत्रफल (Total Surface Area of Hemisphere)
=2πr2+πr2
=3πr2
अतः अर्धगोले का कुल पृष्ठीय का क्षेत्रफल =3πr2
OMR (One Minute Revision)
| आकृति | वक्र पृष्ठीय क्षेत्रफल (वर्ग इकाई) | सम्पूर्ण पृष्ठीय क्षेत्रफल (वर्ग इकाई) | |
|---|---|---|---|
| गोला | 4πr2 | − | r= गोले की त्रिज्या |
| अर्धगोला | 2πr2 | 3πr2 | r= अर्धगोले की त्रिज्या |
उदाहरण 8
एक गोलाकार गुब्बारे में हवा भरने पर, उसकी त्रिज्या 7 सेमी. से बढ़कर 14 सेमी. हो जाती है। इन दोनों स्थितियों में, गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हवा भरने से पहले त्रिज्या r1=7 cm
हवा भरने के बाद त्रिज्या r2=14 cm
हम जानते हैं की, गोले का पृष्ठीय क्षेत्रफल =4πr2
7 cm त्रिज्या वाले गोलाकार गुब्बारे का पृष्ठीय क्षेत्रफल A1=4π×72 cm2
14 cm त्रिज्या वाले गोलाकार गुब्बारे का पृष्ठीय क्षेत्रफल A2=4π×142 cm2
∴A1A2=4π×724π×142
⇒A1A2=4π×494π×196
implies (A_(1))/(A_(2))=(cancel (4pi)xx49)/(cancel (4pi)xx196)
⇒A1A2=14
⇒A1:A2=1:4
अतः गुब्बारे का पृष्ठीय क्षेत्रफल का अनुपात 1:4 हैं।
उदाहरण 9
एक 21 सेमी त्रिज्या वाले अर्धगोले का वक्र पृष्ठीय क्षेत्रफल और सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिये।
हम जानते हैं कि r त्रिज्या वाले अर्धगोले का पृष्ठीय क्षेत्रफल 2πr2 और सम्पूर्ण पृष्ठीय क्षेत्रफल 3πr2 हैं।
यहाँ, त्रिज्या r= 21 cm
अर्धगोले का वक्र पृष्ठीय क्षेत्रफल =2πr2
=2×227×(21)2 cm2
=2×227×21×21 cm2
=2772 cm2
अर्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल =3πr2
=3×227×(21)2 cm2
=3×227×21×21 cm2
=4158 cm2
अतः अर्धगोले का वक्र पृष्ठीय क्षेत्रफल 2772 cm2 तथा सम्पूर्ण पृष्ठीय क्षेत्रफल 4158 cm2 हैं।
घनाभ और घन का आयतन
यदि किसी घनाभ की लंबाई, चौड़ाई तथा ऊँचाई क्रमशः l,b,h हैं, तब
घनाभ का आयतन = लंबाई × चौड़ाई × ऊँचाई
∴ घनाभ का आयतन =l×b×h
चूंकि हम जानते हैं की घन की लंबाई, चौड़ाई तथा ऊँचाई तीनों समान होती हैं।
∴l=b=h=a (माना )
अतः घन का आयतन =a×a×a=a3
Note: आयतन का मात्रक (unit) घन लम्बाई का मात्रक होता है, जैसे - घन मिमी, घन सेमी, घन मीटर आदि।
उदाहरण 10
8 m लंबा, 6 m चौड़ा और 3 m गहरा एक घनाभाकर गड्ढा खुदवाने में 30 रुपए प्रति m3 की दर से होने वाला व्यय ज्ञात कीजिए।
माना गड्ढे की लंबाई l चौड़ाई b तथा ऊँचाई h हैं।
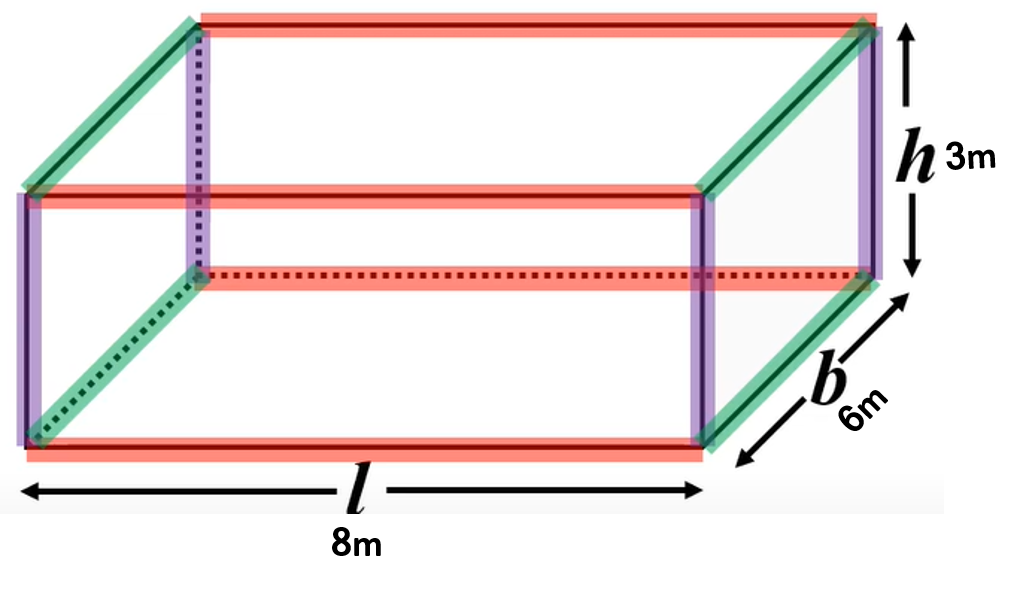
दिया हैं,
गड्ढे की लंबाई l=8 m, चौड़ाई b=6 m और गहराई h=3 m है।
घनाभाकर गढ्ढे का आयतन =l×b×h
=8×6×3
=144m3
अब, 1m3 खुदाई करने का व्यय =₹30
∴ 144m3 खुदाई करने का व्यय =₹144×30=₹4320
अतः, गड्ढा खुदवाने में होने वाला व्यय ₹ 4320 है।
उदाहरण 11
एक गॉंव जिसकी जनसंख्या 4000 है प्रतिदिन प्रति व्यक्ति 150 लीटर पानी की आवश्यकता है। इस गॉंव में 20m×15m×6m मापों वाली एक टंकी बनी हुई है। इस टंकी का पानी वहाँ कितने दिन के लिए पर्याप्त होगा ?
प्रतिदिन प्रति व्यक्ति पानी की आवश्यकता = 150 लीटर
प्रत्येक दिन 4000 व्यक्तियों के लिए पानी की आवश्यकता =4000×150 लीटर
टंकी का आयतन =l×b×h
=(20×15×6)m3
=20×15×6×1000 लीटर , [∵1m3=1000 लीटर ]
∴ टंकी का पानी जितने दिनों के लिए पर्याप्त होगा उसकी संख्या
=20×15×6×10004000×150=3
अतः टंकी का पानी 3 दिनों के लिए पर्याप्त होगा।
बेलन का आयतन
माना कि लंब वृत्तीय बेलन की ऊँचाई h, आधार की त्रिज्या r तथा आयतन V है।
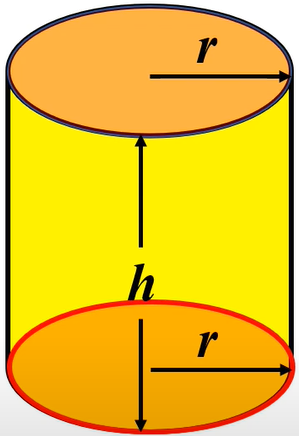
बेलन का आयतन = आधार का क्षेत्रफल × ऊँचाई
V=πr2×h
अतः बेलन का आयतन V=πr2h
उदाहरण 12
एक 44 सेमी × 20 सेमी आयताकार कागज़ के पैन को बेलन बनाने के लिए इसकी लम्बाई के सापेक्ष लपेटा गया है इस प्रकार बनाये गए बेलन का आयतन ज्ञात कीजिए।
दिया है,
बेलन की ऊँचाई h=20 सेमी

चूंकि आयताकार कागज़ के पैन को बेलन बनाने के लिए इसकी लम्बाई के सापेक्ष लपेटा गया है।
अतः बेलन की परिधि =44 सेमी
⇒2πr=44
⇒2×227×r=44
⇒447×r=44
impliescancel (44)/(7)xxr=cancel (44)
⇒ त्रिज्या r=7 सेमी
∴ बेलन का आयतन =πr2h
=227×(7)2×20
=(22)/cancel (7)xx7xxcancel (7)xx20
=3080 सेमी 3
अतः बेलन का आयतन 3080 सेमी 3 हैं।
उदाहरण 13
यदि एक बेलन वाले का पार्श्व पृष्ठीय क्षेत्रफल 94.2 सेमी 2 है और उसकी ऊँचाई 5 सेमी है, तो ज्ञात कीजिए :
(i ) आधार की त्रिज्या
(ii ) बेलन का आयतन (π=3.14 लीजिए )
दिया है,
बेलन के पार्श्व पृष्ठ का क्षेत्रफल =94.2 cm2
तथा बेलन की ऊँचाई h= 5 cm
अत: दिये गये बेलन के आधार की त्रिज्या और बेलन का आयतन = ?
(i) आधार की त्रिज्या
हम जानते हैं कि,
एक बेलन के पार्श्व पृष्ठ का क्षेत्रफल =2πrh
अत: दिये गये बेलन का पार्श्व पृष्ठीय क्षेत्रफल =2×227×r×5
⇒94.2=2×3.14×r×5 cm
⇒94.2=6.28×r×5 cm
⇒94.2=6.28×r×5 cm
⇒94.2=31.4r cm
⇒r=94.231.4
⇒r=3 cm
अत: दिये गये बेलन के आधार की त्रिज्या 3 cm हैं।
(ii) बेलन का आयतन
हम जानते हैं कि,
एक बेलन का आयतन =πr2h
अत: दिये गये बेलन का आयतन =3.14×32×5
=3.14×9×5
=141.3 cm3
अत: दिये गये बेलन के आधार की त्रिज्या = 3 cm और दिये गये बेलन का आयतन = 141.3 cm3
लंब वृत्तीय शंकु का आयतन
यदि किसी शंकु की त्रिज्या r, ऊँचाई h तथा तिर्यक ऊँचाई l है, तो
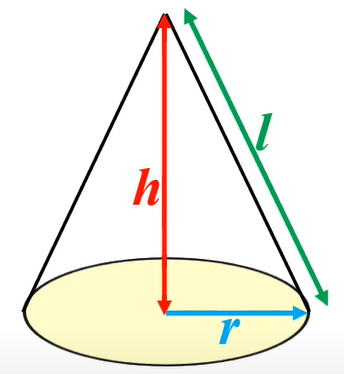
लंब वृत्तीय शंकु का आयतन =13×πr2h=13πr2h
(शंकु का आयतन बेलन के आयतन का एक तिहाई होता हैं क्योंकि बेलन के आयतन =πr2h होता हैं।)
लम्ब वृत्तीय शंकु की तिर्यक ऊँचाई,
l2=h2+r2 (पाइथागोरस प्रमेय से)
⇒l=√h2+r2
अतः तिर्यक ऊँचाई l=√h2+r2
उदाहरण 14
एक शंकु की ऊँचाई 15 cm है। यदि इसका आयतन 1570 cm3 है, तो इसके आधार की त्रिज्या ज्ञात कीजिए । (π=3.14 प्रयोग कीजिए )।
दिया है,
शंकु की ऊँचाई h=15 cm
और शंकु का आयतन =1570 cm3
और, π= 3.14
अत: दिये गये शंकु के आधार की त्रिज्या =?
हम जानते हैं कि, एक लम्ब वृत्तीय शंकु का आयतन =13πr2h
अत: दिये गये शंकु का आयतन,
1570 cm3 =13×3.14×r2×h cm
⇒1570 =13×3.14×r2×15
⇒1570 =3.14×r2×5
⇒1570 =r2×15.70
⇒r2=157015.7
⇒r2=100
⇒r=10 cm
अत: दिये गये शंकु की आधार की त्रिज्या =10 cm
गोले का आयतन
यदि किसी गोले की त्रिज्या r है तब
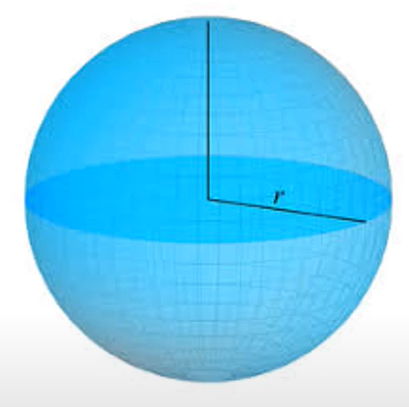
गोले का आयतन =43πr3
गोले का आयतन अर्धगोले के आयतन का आधा होगा।
∴अर्धगोले का आयतन =
अर्धगोले का आयतन =43πr32
=43πr32
=23πr3
अतः अर्धगोले का आयतन =23πr3
OMR (One Minute Revision)
| आकृति | आयतन (घन इकाई) | |
|---|---|---|
| घनाभ | l×b×h | l= लंबाई b= चौड़ाई h= ऊँचाई |
| घन | a3 | a= घन का किनारा | बेलन | πr2h | r= बेलन के आधार की त्रिज्या h= ऊँचाई |
| शंकु | 13πr2h | r= शंकु के आधार की त्रिज्या h= ऊँचाई | गोला | 43πr3 | r= गोले की त्रिज्या |
| अर्धगोला | 23πr3 | r= अर्धगोले की त्रिज्या |
उदाहरण 15
उस गोले का आयतन ज्ञात कीजिए जिसकी त्रिज्या निम्न है : (i) 7 सेमी (ii) 0.63 मीटर
(i) 7 cm
दिया है,
गोले की त्रिज्या =7 cm
अत: दिये गये गोले का आयतन =?
हम जानते हैं कि गोले का आयतन =43πr3
अत: दिये गये गोले का आयतन
=43×227×73
=43×227×7×7×7
= 4/3 xx 22/cancel(7) xx cancel(7)xx7xx7
=43×22×49
=43123
=1437.33 cm3
अत: दिये गये गोले का आयतन =1437.3 cm3
(ii) त्रिज्या =0.63 m
दिया है,
गोले की त्रिज्या =0.63 m
अत: दिये गये गोले का आयतन = ?
हम जानते हैं कि, गोले का आयतन =43πr3
अत: दिये गये गोले का आयतन
=43×227×0.633
=43×227×0.63×0.63×0.63
=4×22×0.09×0.21×0.63
=4×22×0.0119
=1.05 (लगभग)
अत: दिये गये गोले का आयतन लगभग 1.05 m3 हैं।
उदाहरण 16
उस गोले का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm2 है।
दिया है,
गोले का पृष्ठीय क्षेत्रफल = 154 cm2
अत: दिये गये गोले का आयतन =?
हम जानते हैं कि, एक गोले का पृष्ठीय क्षेत्रफल =4πr2
⇒ 154 cm2 =4×227×r2 cm
⇒r2=154×722×4
⇒r=√154×722×4
⇒r=√494
⇒r=72
⇒r=3.5 cm
अत: दिये गये गोले की त्रिज्या =3.5 cm
अब, हम जानते हैं कि, गोले का आयतन
=43×π×r3
=43×227×3.53
=43×227×3.5×3.5×3.5
=179.66 cm3
अत: दिये गये गोले का आयतन = 179.66 cm3
सारांश
| आकृति | वक्र पृष्ठीय क्षेत्रफल या पार्श्व पृष्ठीय क्षेत्रफल (वर्ग इकाई) | सम्पूर्ण पृष्ठीय क्षेत्रफल (वर्ग इकाई) | आयतन (घन इकाई) | |
|---|---|---|---|---|
| घनाभ | 2h(l+b) | 2(l×b+l×h+b×h) | l×b×h | l= लंबाई b= चौड़ाई h= ऊँचाई |
| घन | 4a2 | 6a2 | a3 | a= घन का किनारा | बेलन | 2πrh | 2πr(r+h) | πr2h | r= बेलन के आधार की त्रिज्या h= ऊँचाई |
| शंकु | πrl | πr(l+r) | 13πr2h | r= शंकु के आधार की त्रिज्या l= तिर्यक ऊँचाई h = ऊँचाई | गोला | 4πr2 | − | 43πr3 | r= गोले की त्रिज्या |
| अर्धगोला | 2πr2<td><td>3pi r^2 <td><td>2/3 pi r^3<td><td>r =अर्धगोले की त्रिज्या |