LINEAR EQUATION IN TWO VARIABLES for Class 9 MATHS
INTRODUCTION
Is chapter me hum linear equation with two variables ko detail me padhne wale hai . Aise algebraic equations jisme exactly two variables ho and maximum power or degree of the variables must be one , iss type ke algebraic equation ko linear equation with two variable kehte hai. Guys linear ka matlab hota hai straight line, iska matlab hai If we solve the linear equation with two variables and usse graph me plot kre to hume har condition me ek straight line hi milegi. So iss chapter me hum ye janenge ki kon kon se equations linear equation with two variables hote hai , sath hi sath hum dekhenge solution of linear equation with two variable and usse graph me plot krna , So let's go !
Linear Equations
So guys jaise ki hum pehle se jante hai an algebraic expression is a combination of variables and numbers and at least one mathematical operation like (+,−,× etc), For Ex : 7x3+√x+9, hum ye bhi jante hai ki polynomials are special type of algebraic expression jisme variables ki power hamesa whole number ho i.e.(0,1,2,….). For Ex :7x4+9x3+6. Aap polynomials with one variable bhi dekh chuke hai matlab aise polynomials jisme sirf ek variable hote hai . For example: 7x3+9. Aap ye bhi jante hai ki agar variable ki maximum power ya degree of the polynomial one ho in that case it is known as linear polynomial right!
A linear equation is an equation which involves linear polynomials.
Linear Equation in two variable ko padhne se pahle hum apna discussion Linear Equation in one variable par le jate hai.
Linear Equation in One Variable :
Koi aisa equation jise hum ax+b=0 ke form me likh sakte hai is called Linear Equation in one variable, where a≠0 and b are two real numbers and x is a variable. Iss baat ka dhyan rkhenge ki x ke place pr hum koi dusra variable bhi le sakte hai.
For Ex : 7x+8=0,9x+9=0 etc.
Solution of Linear equation in one variable
Solution of linear equation in one variable ka matlab hai ke hume variable ki aisi value find karni hai jisse L.H.S and R.H.S ki values equal ho jaaye.
Note : There is only one variable in the linear equation in one variable so there will be only one solution for this equation.
Example 1
If (2,0) is a solution of the linear equation 2x+3y=k, then the value of k is
Since, (2,0) is a solution of the given linear equation 2x+3y=k, then put x=2 and y=0 in the equation.
⇒ 2(2)+3(0)=k<br>⇒k=4
Hence, the value of k is 4.
Linear Equation in Two Variables
Ek aisa equation jise hum ax+by+c=0 ke form me likh sakte hai where a,bandc are real numbers and a , b are non zero is called linear equation in two variable. Here x and y are two variable whose values are unknown to us . Yha bhi is baat ka dhyan rkhenge ki xandy ke place pr hum other alphabets bhi le sakte hai like landm, pandq and so on.
For Ex : 7x+9y+8=0, 7x+9y=−8, 8x+9=8y
Note: Yha hum dekh sakte hai ki we have nothing but an algebraic equation jisme xandy, two variables hai and degree of the linear equation is always one.
Example 2
Write each of the following equations in the form ax+by+c=0 and indicate the values of a,b,c in each case.
(i) 2x+3y=4.37
(ii) x−4=√3y
(iii) 4=5x−3y
(iv) 2x=y
(i) We have 2x+3y=4.37⇒2x+3y−4.37=0.
This is of the form ax+by+c=0, where a=2,b=3andc=−4.37.
(ii) x−4=√3y⇒x−√3y−4=0
This is of the form ax+by+c=0, where a=1,b=−√3andc=−4.
(iii) 4=5x−3y
⇒−5x+3y+4=0.
This is of the form ax+by+c=0 where a=−5,b=3andc=4.
(iv) 2x=y⇒2x−y=0.
This is of the form ax+by+c=0, where a=2,b=−1andc=0.
Example 3
Write the linear equation such that each point on its graph has an ordinate 3 times its abscissa.
Let the abscissa of the point be x,
According to the question, Ordinate (y)=3× Abscissa⇒y=3x
⇒3x−y=0
Which is the required linear equation in two variables.
Linear equations and Cartesian Plane
Aapke mind me ye question aata hoga ki why this is called a linear equation to iska zawab hai ki when we solve this equation for xandy sath hi sath un values ki help se Cartesian plane pr points locate krte hai to ek interesting baat samne aati hai ki wo sare points kise ek straight line par lie karte hai that is why ise linear equation kehte hai jise hum aage dekhenge.
Solution of Linear Equation in Two Variables
So guys, aapne dekha ki jab humare pas linear equation in one variable tha in that case humare pas ek unique solution hua karta tha lekin jab humare pas two variables hai to uss condition mein solution means a pair of values one for x and one for y which will satisfy the given equation.
For Ex : Let us consider we have a linear equation in two variables i.e. 3x+6y=9 , we have to solve this for x and y.
Given equation is 3x+6y=9, ise solve krne ke liye hum sabse pehle to x ya y kise bhi ek variable ki kuch values khud se decide kr lenge and with respect to those values dusre variable ki values find out kr lenge. Jisse hum ek table bna kr bhi represent kr sakte hai and Cartesian plane pr bhi represent kr sakte hai.
For x=0
3x+6y=9⇒3×0+6y=9⇒6y=9
∴y=96=32
For x=1
3x+6y=9⇒3×1+6y=9⇒6y=9−3
∴6y=6
So, y=1
For x=2
3x+6y=9⇒3×2+6y=9⇒6+6y=9
∴6y=9−6⇒y=36
So y=12
In values ko hum tabulate bhi kr sakte hai. (See the table below) 
Note: Here we can see that for different values of x we have different values of y and vice versa. To ye dekhna bahut in interesting hai ki hum x ki kitni bhi values assume kar skate hai jiske liye hume different y ki values milegi. Iska matlab ki total number of solutions, two variable ke case me infinite honge .
Sath hi sath hum ye bhi observe krte hai ki x and y ki different values ek unique pair ka formation krte hai and that pair is nothing but the coordinate of a point on a Cartesian plane.
Example 4
Find four different solutions of the equation x+2y=6.
We have x+2y=6
Putting x=0
We get 0+2y=6
⇒y=62=3
∴(0,3) is a solution.
Putting y=0
We get x+2×0=6
⇒x=6
∴(6,0) is a solution.
Now putting x=1
We get 1+2y=6
⇒2y=6−1=5
∴y=52
∴(1,52) is a solution.
Putting y=1
We get x+2×1=6
⇒x=6−2
⇒x=4
∴(4,1) is a solution.
Example 5
Check which of the following are solutions of the equations x−2y=4 and which are not :
(i) (0,2) (ii) (2,0) (iii) (4,0) (iv) (√2,4√2) (v) (1, 1)
The given equation may be written as x−2y−4=0. …(A)
(i) Putting x=0 and y=2 in (A), we get
LHS=(0−2×2−4)=(0−4−4)=−8≠0=RHS.
∴(0,2) is not a solution of x−2y=4.
(ii) Putting x=2andy=0 in (A), we get
LHS={2−2×(0)−4}={2−0−4}=−2≠0=RHS.
∴(2,0) is not a solution of x−2y=4.
(iii) Putting x=4andy=0 in (A), we get
LHS=(4−2×0−4)=0=RHS.
∴(4,0) is a solution of x−2y=4.
Q. Iske aake ke questions aap khud se try krenge.
Graph of linear equation in two variables
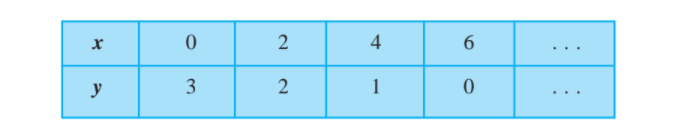
Jaisa ki hum Solution of linear equation in two variables nikalna sikh chuke hai sath hi sath hm ye jante hai ki solution of linear equation in two variable is always in the form of pairs jo Cartesian plane ke ek point ko represent karte hai . Now let us look their geometric representation. Let us Consider a Linear equation in two variable i.e. x+2y=6
Solution of of the above linear equation can be expressed in the form of table right!
Let us plot the points (0,3),(2,2),(4,1),(6,0) on the graph paper
Yha hum dekh sakte hai ki sare points ko connect karne se we will have a straight line. Or ye observe krna bahut hi interesting hai ki aage jitney bhi solutions hum find- out krte hai is particular linear equation ke liye wo ise line pr lie krte hai. Or jaise ki aap jante hai ki kise line pr hazaron points ho sakte hai that means kise linear equation in two variable ke hazaron solutions bhi ho sakte hai.
In fact, a linear equation in two variables is represented geometrically by a line whose points make up the collection of solutions of the equation. This is called the graph of the linear equation.
Note :To obtain the graph of a linear equation in two variables, it is enough to plot two points corresponding to two solutions and join them by a line. Kyuki hum aache se jante hai ki kise line ko construct krne ke liye we need only two points.
Example 6
Draw the graph of the equation 2x+3y=11. From your graph, find the value of y when (a)x=7,(b)x=−8.
We have
2x+3y−11⇒y=(11−2x)3. …(i)
Putting x=1, we get y=(11−2×1)3=93=3.
Putting x=4, we get y=(11−2×4)3=33=1.
Putting x=−2,we get y={11−2×(−2)}3=153=5.
Putting x=−5,we get y={11−2×(−5)}3=213=7.
Thus, we have the following table: x14−2−5y3157
On a graph paper, draw lines X'OX and YOY' as the x-axis and the y-axis respectively.
On this graph paper, plot the pointsA(1,3),B(4,1),C(−2,5)andD(−5,7). Join AB, AC and CD, to get the straight line BACD. Produce it in both ways to get the required graph.
(a) On the x-axis, we take a point P for which x=7, i.e., OP=7.
From P, draw PE⊥X'OX, meeting DCAB produced at E(7,-1).
∴(x=7⇒y=−1). Thus, when x=7, then y=-1.
(b) On the x-axis, we take a point Q on LHS of the y-axis, such that OQ=x=-8.
From Q, draw QF⊥X'OX, meeting BACD produced above at F(-8,9).
∴(x=−8⇒y=9). Thus, when x=-8,then y=9.
Equations of Lines Parallel to the x-axis and y-axis
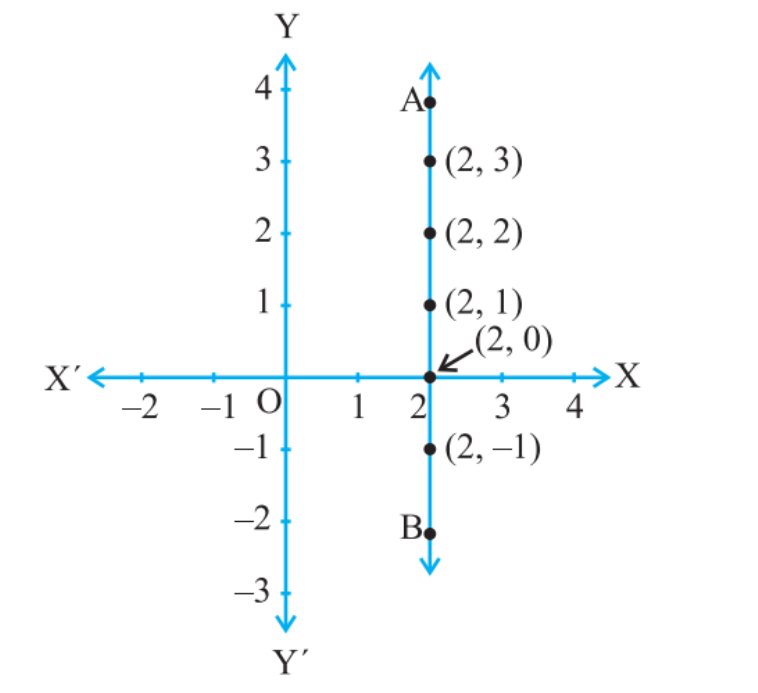
Consider an equation x−2=0, ise standard form me likhne se hume x−0×y−2=0 milta hai
Yha dekho friends aap, y ki koi bhi value rkhte hai 0×y=0 ho jayega and hume har condition me x=2 hi milega right !
To guys aap ye dekh sakte hai ki hume ek line milti hai which is parallel to Y-axis. Is se hum ye conclusion pe pahunchte hai ki if y term is zero in a linear equation in two variable, then we will have a parallel line with Y-axis.
Similarly if x term is zero in a linear equation of two variable, we will have a line parallel to X- axis.
Example 7
A taxi charges .Rs 20 for the first kilometre and @ .Rs per km for subsequent distance covered. Taking the total distance covered as x km and total fare .Rs y, write a linear equation depicting the relation between x and y. Draw the graph between x and y.
Form your graph, find the taxi charges for covering
(a) 12 km and (b) 20 km.
The required linear equation is given by
y=20+12(x−1)⇒y=8+12x …(i)
Putting x=1 in (i), we gety=(8+12×1)=20.
x=6 in (i), we get y=(8+12×6)=80.
Putting x=10 in (i) , we get y=(8+12×10)=128.
Putting x=15 in (i), we get y=(8+12×15)=188.
Thus, we have the following table: x161015y2080128188
On a graph paper, draw lines X'OX and YOY' as the x-axis and the y-axis respectively. Choose the scale.
Along the x-axis: 1 small division = 1 km.
Along the y-axis : 5 small division = .Rs 40.
Now, the plot the points A(1,20),B(6,80),C(10,128)andD(15,188).
Join AB, BC and CD to get the single graph line AD, as shown below.
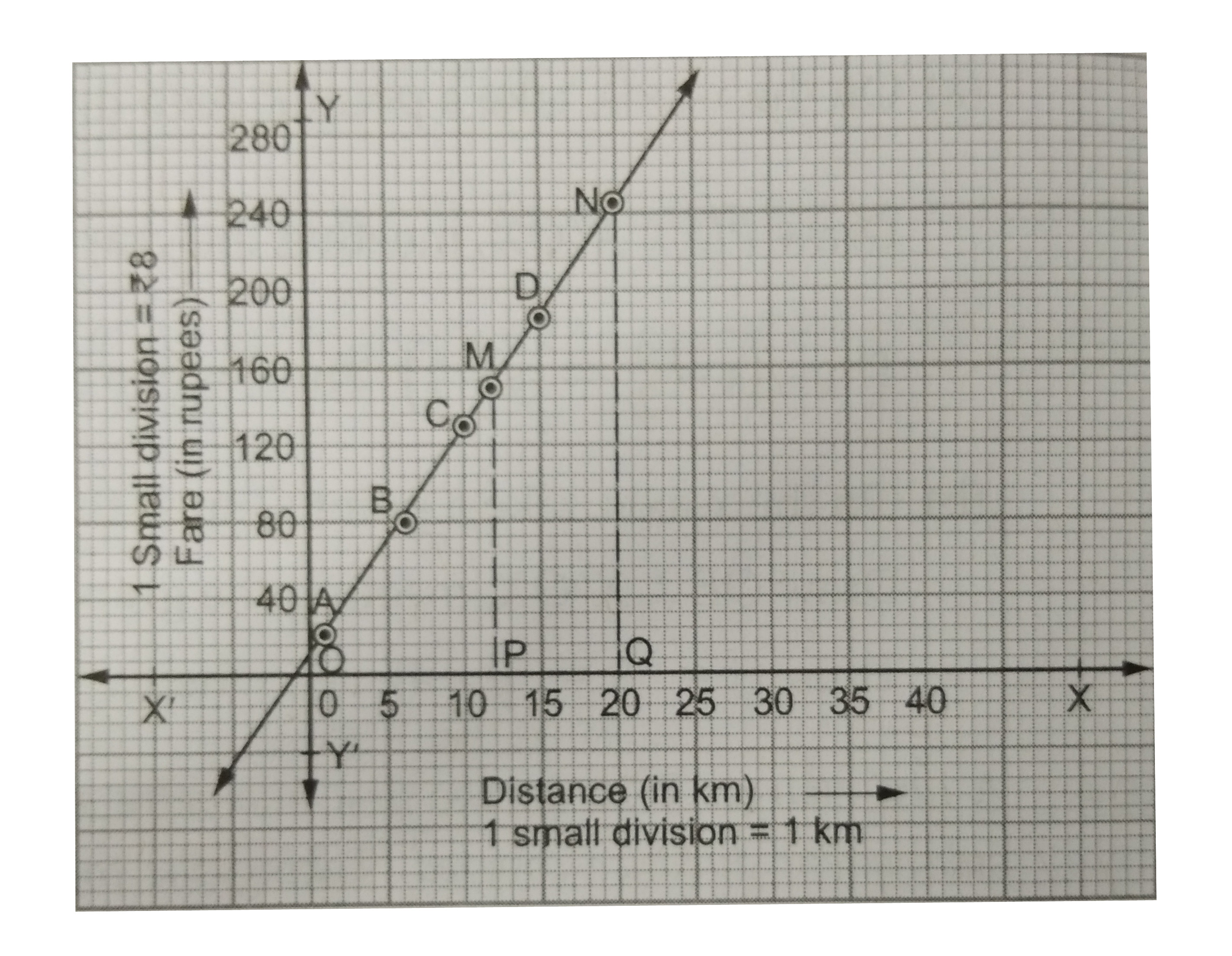
(a) On the x-axis , take a point P such that OP=12 km.
Draw PM⊥X'OX meeting the graph line at M(12,152).
Thus (x=12⇒y=152), i.e., when distance covered is 12 km then the taxi -fare is .Rs 152.
(b) On the x- axis, take a point Q such that OQ = 20 km.
Draw QN⊥X'OX, meeting the graph line at N(20,248).
Thus ,(x=20⇒y=248) i.e., when distance covered is 20 km then the taxi -fare is .Rs 248.
Summary
In this chapter, you have studied the following points :
(i). An equation of the form ax+by+c=0, where a, b and c are real numbers, such that a and
b are not both zero, is called a linear equation in two variables.
(ii). A linear equation in two variables has infinitely many solutions.
(iii). The graph of every linear equation in two variables is a straight line.
(iv). x=0 is the equation of the y-axis and y=0 is the equation of the x-axis.
(v). The graph of x=a is a straight line parallel to the y-axis.
(vi). The graph of y=a is a straight line parallel to the x-axis.
Note: An equation of the type y=mx represents a line passing through the origin.
(vii).Every point on the graph of a linear equation in two variables is a solution of the linear equation. Moreover, every solution of the linear equation is a point on the graph of the linear equation.
Let's Revise
For Ex: 7x+8=0, 9x+9=0, etc.
For Ex :7x+9y+8=0, 7x+9y=−8, 8x=8y
Let us Consider a Linear equation in two variable i.e. x+2y=6
Solution of of the above linear equation can be expressed in the form of table right!
Let us plot the points (0,3),(2,2),(4,1),(6,0) on the graph paper 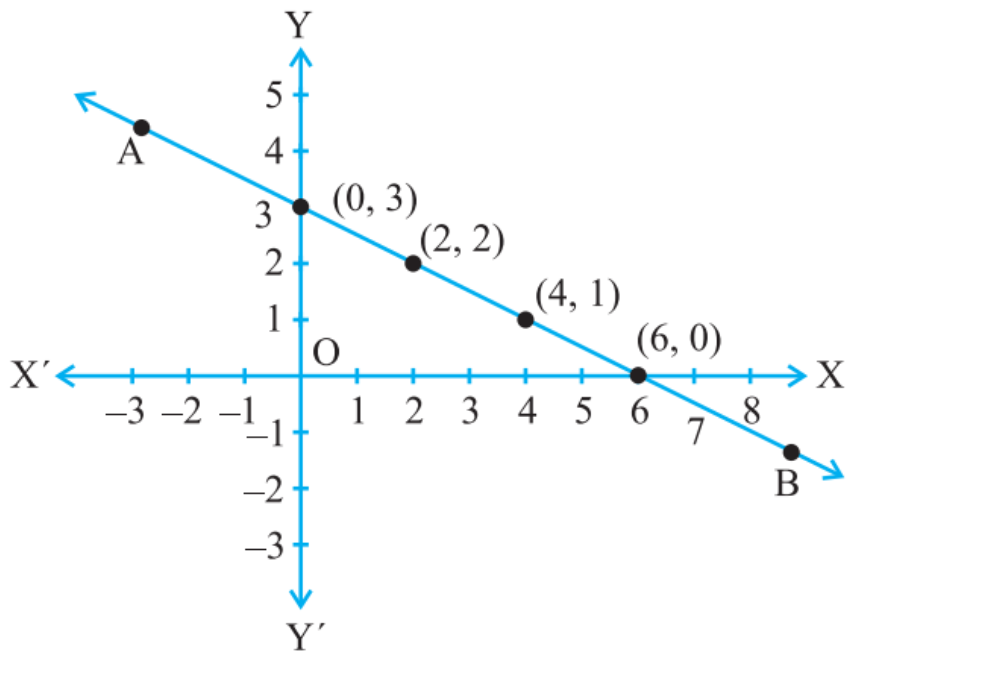
Yha hum dekh sakte hai ki sare points ko connect karne se we will have a straight line.
Note:To obtain the graph of a linear equation in two variables, it is enough to plot two points corresponding to two solutions and join them by a line.
If y term is zero in a linear equation in two variable, then we will have a parallel line with Y-axis
Similarly if x term is zero in a linear equation of two variable, we will have a line parallel to X- axis.
For Example: x−2=0
Ise standard form me likhne se hume x−0×y−2=0 milta hai
Yha dekho friends aap, y ki koi bhi value rkhte hai 0×y=0 ho jayega and hume har condition me x=2 hi milega right !
Yha hum dekh sakte hai ki hume ek line milti hai which is parallel to Y-axis. Similarly line will be parallel to x-axis if x term is zero in the equation.