SURFACE AREAS AND VOLUMES for Class 9 MATHS

Hello Bachcho, aap apne aas paas normally jo bhi dekhte ho wo solid form ki hoti hai. Hum apni studies mai unn sabhi figures se deal karte hai jo easily hum apni notebook ya blackboard par draw kar sakte hain. Inn sab ko plane figures kehte hai. Hum already samajh chuke hai ki square, rectangle, circle kya hota hai aur inke perimeters, area kaise nikalte hai. Yeh sab hum apni phechli classes mai padh chuke hain. Aur bachcho ye dekhna bahot hi zyada interesting hoga ki if we cut out many of these plane figures of the same shape and size from cardboard sheet and stack them up in a vertical pile. Iss process se aapko kuch new figures dekhne ko milenge jaise ki cube, cuboid, cylinder, etc. Aapne earlier classes mai inke bare mai thoda bahot padha hua hai. Toh ab iss chapter mein hum different figures ka surface area and volume detail mai nikalna sikhenge with very interesting and different examples.

Toh bachcho iss chapter mai hum surface area and volume of different solid shapes such as the cube, cuboid, cone, cylinder, and so on. Surface area ko generally lateral surface area (LSA), curved surface area (CSA) and total surface area (TSA) mai divide kiya gaya hai. Abh aage hum different three dimensional shapes ke surface area ke formulas and volumes ke formulas ko detail mai padhenge. Iss chapter mai hum two shapes ke combination ko bhi padhenge. It would be very interesting to study all these combination.

The surface area of any given object is the area or region occupied by the surface of the object. Whereas volume is the amount of space available in an object. In geometry, there are different shapes and sizes such as sphere, cube, cuboid, cone, cylinder, etc.

Toh bachcho ek example ke through hum surface area of cuboid ko samjhenge.
Kya aapne bahot sari sheets ka bundle dekha hai? kaisa dikhta hai?
Agar aapko nahi pata toh aap iss image mai dekh sakte hai.

Toh jaisa ki aap dekh sakte hai ki yeh ek cuboid ki tarah dikh raha hai. Toh abh hume yeh dekhna hai ki agar hum iss bundle ko cover karna chahte hai to kitne paper ki zarurat padegi? Toh chalo dekhte hai :-
(a) Sabse pehle hume ek rectangular sheet lenge bottom ke liye taki sari sheets uske upar rakhi jaye.

(b) Abh hum two long rectangular sheets lenge taki hum uss sheet ke dono side mai laga sake.

(c) Abh hume front aur back ends ko cover karne ke liye, we would need two more rectangular pieces of a different size.

(d) Abh tak humne jo bhi banaya hai abh hum usko ek baar open karke dekhenge. Toh wo kuch (below image) aisa dikhega.

(e) Abh hume iske top ko cover karne ke liye bhi same size ka rectangular piece chahiye jo humne bottom mai liya tha, aur agar hum usko right side mai lgayenge to wo kuch (below image) aisa dikhega.

(f) So we have used six rectangular pieces to cover the complete outer surface of the cuboid.

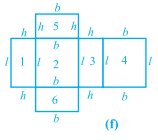
A cuboid is a box-like shape. It has six rectangular faces. The faces opposite each other are equal.
This shows us that the outer surface of a cuboid is made up of six rectangles (in fact, rectangular regions, called the faces of the cuboid), whose areas can be found by multiplying length by breadth for each of them separately and then adding the six areas together.
Now, if we take the length of the cuboid as $l$, breadth as $b$ and the height as $h.$
So, the sum of the areas of the six rectangles is:
Area of rectangle $1(=l\times h)$
$+$
Area of rectangle $2(=l\times b)$
$+$
Area of rectangle $3(=l\times h)$
$+$
Area of rectangle $4(=l\times b)$
$+$
Area of rectangle $5(=b\times h)$
$+$
Area of rectangle $6(=b\times h)$
$+$
$=2(l\times b)+2(b\times h)+2(l\times h)$
$=2(lb+bh+hl)$
This gives,

where $l,b$ and $h$ are respectively the three edges of the cuboid.
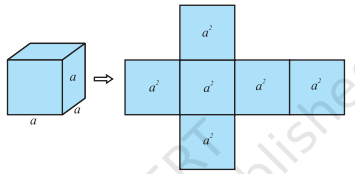
Toh bachcho aapne abh tak upar sirf cuboid ke barein mai padha hai abh hum cube ke barein mai padhenge.
Recall that a cuboid, whose length, breadth and height are all equal, is called a cube. If each edge of the cube is $a$, then the surface area of this cube would be
$2(a\times a+a\times a+a\times a)$, i.e., $6a$

where $a$ is the edge of the cube.
Abh aap suppose kare ki cuboid ke six faces mai se hum only four faces (leaving top and bottom) ka hi area find karenge. So, the area of these four faces is called the lateral surface area of the cuboid.
So, lateral surface area of a cuboid of length $l,$ breadth $b$ and height $h$ is equal to $2lh+2bh\text{or}2(l+b)h.$
Similarly, lateral surface area of a cube of side $a$ is equal to $4a^2.$

The surface area of a cuboid (or a cube) is sometimes also referred to as the total surface area.

• A cuboid has $6$ faces, $8$ vertices, and $12$ edges.
• All the angles formed at the vertices of a cuboid are right angles.
• All the faces of a cuboid are rectangular in shape.
• Two diagonals can be drawn on each face of a cuboid.
• The opposite edges of a cuboid are parallel to each other.
• The dimensions of a cuboid are length, width, and height.

• A cube has $12$ edges, $6$ faces, and $8$ vertices.
• All the faces of a cube are shaped as a square hence the length, breadth, and height are the same.
• The angles between any two faces or surfaces are ${90}^{\circ }$.
• The opposite planes or faces in a cube are parallel to each other.
• The opposite edges in a cube are parallel to each other.

Three cubes each of side $5cm$ are joined end to end. Find the surface area of the resulting cuboid.

If we join these three cubes, then the length of the resulting cuboid will be $5+5+5=15cm$.
Breadth and height will be $5cm$.
$\therefore$ Surface area of the cuboid will be,
$S=2(lb+bh+hl)=2(15\cdot 5+5\cdot 5+5\cdot 15)=2\left(175\right)=350c{m}^2.$

The sum of length, breadth and depth of a cuboid is $19cm$ and the length of its deagonal is $11cm.$
Find the surface area of the cuboid.

Let length be $l$
Let breath be $b$
Let height be $h$
$l+b+h=19$
Length of diagonal$=\sqrt{l^2+b^2+h^2}$
$11=\sqrt{l^2+b^2+h^2}$
${11}^2=l^2+b^2+h^2$
${11}^2={19}^2-2(lb+lh+hl)$
surface area of cuboid$={19}^2-{11}^2$
$=240c{m}^2$.

Agar hum bahot sari circular sheets ko ek dusre ke upar stack kare jaise ki humne rectangular sheets ko kiya tha toh wo kuch (below image) aisa dikhega.

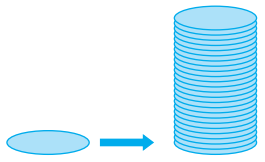
Agar hum continuously sheets ko vertically stack karte hai toh, we get what is called a right circular cylinder. Because it has been kept at right angles to the base, and the base is circular.
Toh bachcho abhi aapne padha ki right circular cylinder kaisa hota hai but abh aap dekhoge ki kis tarah ke cylinder right circular cylinder nahi hote.

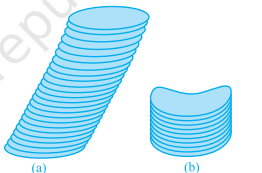
Aap figure (a) ko dekho wo aapko ek cylinder ki shape mai dikhega lekin wo right circular cylinder nahi hai because it is not at right angles to the base.
Figure (b) mai uska base hi circular nahi hai toh wo automatically right circular cylinder nahi hai.
Toh chalo uss paper sheets ke bundle ke cylinder ko cover karte hain. How will we do it with the minimum amount of paper?
Toh sabse pehle aap ek rectangular sheet le lijiye, whose length is just enough to go round the cylinder and whose breadth is equal to the height of the cylinder.

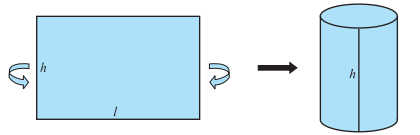
The area of the sheet gives us the curved surface area of the cylinder. Note that the length of the sheet is equal to the circumference of the circular base which is equal to $2\pi r.$
So, curved surface area of the cylinder
$=$ area of the rectangular sheet $=$ length $\times$ breadth
$=$ perimeter of the base of the cylinder $\times$ h
$=$ $2\pi r\times h.$

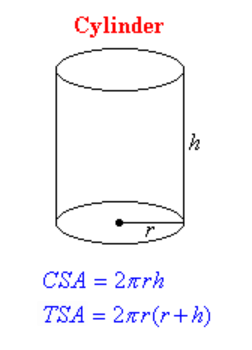
where $r$ is the radius of the base of the cylinder and $h$ is the height of the cylinder.
Agar hum cylinder ka top aur bottom dono cover karna chahte hai toh hume two circles chahiye, each of radius $r$, and area is $\pi r^2$, giving us the total surface area as $2\pi rh+2\pi r^2=2\pi r(r+h).$
$\pi =\frac{22}{7}\text{or}3.14$

where $h$ is the height of the cylinder and $r$ its radius.

• It has two curved edges, one curved surface, and two flat faces.
• Cylindrical bases always are congruent to each other.
• The base and the top of the cylinder always are identical to each other.

The inner diameter of a circular well is $3.5m.$ It is $10m$ deep.
Find (i) Its inner curved surface area,
(ii) The cost of plastering this curved surface at the rate of $Rs40$ per $m^2$.

1) CSA=$2\pi rh$
=$2\times \frac{22}{7}\times {\left(\frac{3.5}{2}\right)}^2\times 10$
=$110m^2$
2)$1m^2=40Rs$
$110m^2=110\times 40Rs$
$=4400Rs$

In a hot water heating system, there is a cylindrical pipe of length $28m$ and diameter $5cm.$ Find the total radiating surface in the system.

Radiating Surface=CSA of given cylinder
=$2\pi rh$
=$2\cdot \frac{22}{h}\cdot 0.05\cdot 28$
=$4.4m^2$.

A right circular cone is one whose axis is perpendicular to the plane of the base. We can generate a right cone by revolving a right triangle about one of its legs.

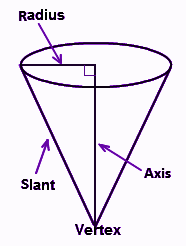
Iss figure mai aap ek right circular cone dekh sakte ho aur ek circular base jiska radius $r$ hai aur iski axis base ke perpendicular hain. Jo line vertex ko base ke center se connect karti hai wo height of the cone kehlati hai. The length at the outer edge of the cone, which connects a vertex to the end of the circular base is the slant height.
For a right circular cone of radius ‘r’, height ‘h’ and slant height ‘l’, we have;

Formula of slant height is
$l=\sqrt{r^2+h^2}$
Agar hume cone ke base yani circular portion ka bhi area nikalana ho to hume iske curved surface area mai circle ke area ko bhi add karna padega.
$=\pi r^2+\pi rl$
$=\pi r(r+l)$

• It has a circular base. The axis is a line that joins the vertex to the center of the base.
• The slant height of the cone is measured from the vertex to the edge of the circular base. It is denoted by $l$ or $s$.
• The altitude or height of a right cone coincides with the axis of the cone and is represented by $h$.
• If a right triangle is rotated with the perpendicular side as the axis of rotation, a right circular cone is constructed. The surface area generated by the hypotenuse of the triangle is the curved surface or the lateral surface area.

Find the curved surface area of a right circular cone whose slant height is $10cm$ and base radius is $7cm.$

CSA=$\pi rl$
=$\frac{22}{7}\times 7\times 10$
=$220c{m}^2$.

A joker’s cap is in the form of a right circular cone of base radius $7cm$ and height $24cm.$
Find the area of the sheet required to make $10$ such caps.

Curved surface Area of cone=$\pi \times r\times l$
where $r\text{and}l$ are the radius and slant height of the cone
slant height=$l=\sqrt{r^2+h^2}$
given $r=7cm$ and $h=24cm$ thus slant height $=25cm.$
Curved surface Area of cone=$=\pi \times 7\times 25=550{\left(cm\right)}^2$

Bachcho aapke mind mai sphere aur circle ko lekar kafi sare questions aate honge.
Jaise ki sphere kya hai? Kya circle aur sphere same hai?
Kya aap circle ko ek paper par draw kar sakte hai? The answer is yes. Because circle ek plane closed figure hai jiske sare points ek constant distance (center) se form hote hai. Agar aap ek string ko circular arc ke diameter ke sath tie karke usko rotate karte hai to aap ek solid dekhoge.
Now the question is kya yeh solid ek sphere hai? So, the answer is $yes.$

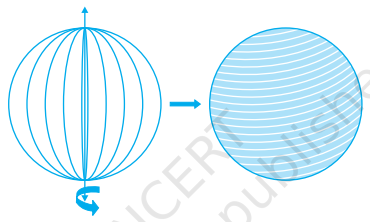
Can you guess circle ke center ka kya hota hai jab wo sphere ban jata hai. Of course, it becomes the centre of the sphere. Sphere ek three dimensional figure hai, which is made up of all points in the space, which lie at a constant distance called the radius, from a fixed point called the centre of the sphere.
Sphere ke outer surface ko surface area of sphere kehte hai.

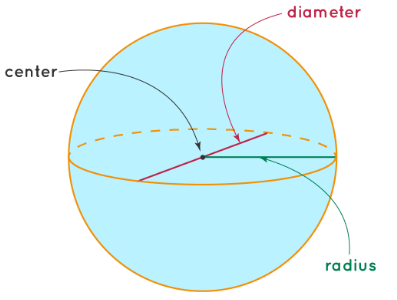
Circle aur sphere mai main difference yeh hai ki circle 2 dimensional hota hai aur sphere 3 dimensional hota hai. Yeh formula Archimedes ne diya tha. Now we will see the relation between cylinder and sphere.
Agar cylinder aur sphere ka radius $r$ hai to sphere ka surface area aur cylinder ka lateral surface area equal hoga.
Surface Area of Sphere = Lateral Surface Area of Cylinder
$\Rightarrow$ The surface area of Sphere = $2\pi rh$
Height of cylinder = Diameter of sphere = $2r$
Surface area of sphere is $2\pi rh=2\pi r\left(2r\right)=4\pi r^2$ square units.

How many faces do you see in the surface of a sphere?
There is only one, which is curved.
Abh hum ek sphere lenge aur ushe ekdum centre se plane ke through cut kar lenge.


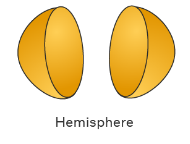
Yes, it gets divided into two equal parts.
What will each half be called?
It is called a hemisphere.
Hemisphere ke two faces hai ek curved face and dusra flat face (base). The curved surface area of a hemisphere is half the surface area of the sphere, which is $\frac{1}{2}of4\pi r^2.$

Where $r$ is the radius of the sphere of which the hemisphere is a part.
Now taking the two faces of a hemisphere, its surface area
$2\pi r^2+\pi r^2$

• A sphere is perfectly symmetrical.
• All the points on the surface are equidistant from the centre.
• It does not have a surface of centres.
• It has a constant width and circumference.

• A hemisphere has a one curved surface area.
• Just like a sphere, there are no edges and no vertices in a hemisphere.
• The diameter of a hemisphere is a line segment that passes through the center and touches the two opposite points on the surface of the hemisphere.
• It is created when a plane intersects the center of a sphere cutting it into two equal halves.

A sphere is like the surface of a ball. The word solid sphere is used for the solid whose surface is a sphere.

Find the radius of a sphere whose surface area is $154c{m}^2$

We know surface area of a sphere can be given by,
$A=4\pi r^2$
So, $4\pi r^2=154$
$\Rightarrow 4\times \frac{22}{7}\times r^2=154$
$\Rightarrow r^2=\frac{154\times 7}{22\times 4}=\frac{49}{4}$
$\Rightarrow r=\sqrt{\frac{49}{4}}=\frac{7}{2}=3.5$
So, radius of sphere will be $3.5cm$.

Find the surface area of a sphere of radius: (i) 10.5 cm (ii) 5.6 cm (iii) 14 cm

The surface area of a sphere can be given as $S=4\pi r^2$
(i) Here, $r=10.5cm$
So, $S=4\times \frac{22}{7}\times 10.5\times 10.5$
$=132\times 10.5=1386c{m}^2$

(ii)Here, $r=5.6cm$
So, $S=4\times \frac{22}{7}\times 5.6\times 5.6$
$=88\times 0.8\times 5.6=394.24c{m}^2$

(iii)Here, $r=14cm$
So, $S=4\times \frac{22}{7}\times 14\times 14$
$=88\times 28=2464c{m}^2$

The volume of a cuboid can be found by multiplying the base area with the height.
Therefore,
Volume of the cuboid = (length × breadth × height) cubic units.

The volume of the cube is equal to the product of the area of the cube and height. Jaisa ki hum jante hai ki cube ke sare edges ki length same rehti hai.
Hence,
Volume of the cube $=l^2\times h$
Since, $l=h$
Therefore,
Volume of the cube = $l^2\times l$
Volume of the cube = $l^3$

A cuboidal water tank is $6m$ long, $5m$ wide and $4.5m$ deep. How many litres of water can it hold? ($1m^3=1000l$)

Water tank can hold water equal to its volume.
As tank is a cuboid in shape, its volume will be ,$V=l\times b\times h$
Here, Length,$l=6m$
Breadth,$b=5m$
Height, $h=4.5m$
So, $V=6\times 5\times 4.5=135m^3$
Also, $1m^3=1000l$
So, $V=1,35,000l$
So, the water tank can hold $1,35,000$ $litres$ of water.

Find the volume, the total surface area and the lateral surface area of a cuboid which is $15m$ long, $12m$ wide and $4.5m$ high.

Here, $l=15m$ , $b=12m$ and $h=4.5m$
Volume of the cuboid $=(l\times b\times h)$ cubic units
$=(15\times 12\times 4.5)m^3=810m^3$
Total surface area of the cuboid
$=2(lb+bh+lh)$ sq units
$=2(15\times 12+12\times 4.5+15\times 4.5)m^2=603m^2$
Lateral surface area of the cuboid
$=[2(l+b)\times h]$ sq units
$=[2(15+12)\times 4.5]m^2=243m^2$

Jaisa ki aapne dekha humne rectangular sheets se ek cuboid banaya aur ushi tarah humne circular sheets se cylinder banaya. Toh jaise humne cuboid ke liye argue ki ushi tarah hum cylinder ki volume ko bhi calculate kar sakte hai.
$base\times height$
= area of circular base × height
$=\pi r^{2}h$

Find the (i) Volume,
(ii) Area of curved surface and
(iii) Total surface area of a cylinder having radius of the base $14cm$ and height $30cm.$

Here, $r=14cm$ and $h=30cm$
(i) Volume of the cylinder $=\left(\pi r^{2}h\right)$ cubic units
$=(\frac{22}{7}\times 14\times 14\times 30)c{m}^3=18480c{m}^3$
(ii) Curved surface area of the cylinder $=\left(2\pi rh\right)$ sq units
$=(2\times \frac{22}{7}\times 14\times 30)c{m}^2=2640c{m}^2$
(iii) Total surface area of the cylinder
$=(2\pi rh+2\pi r^2)\text{sq units}=2\pi r(r+h)$ sq units
$=\{2\times \frac{22}{7}\times 14\times (14+30)\}c{m}^2=3872c{m}^2$

The total surface area of a cylinder of radius $7cm$ is $880c{m}^2$.
Find the height and the volume of the cylinder.

Given, $r=7cm.$ Let the height of the cylinder be $h$ cm.
Then, total surface area $=(2\pi r^2+2\pi rh)$ sq units
$=2\pi r(r+h)$ sq units
$=2\times \frac{22}{7}\times 7\times (7+h)c{m}^2$
$=44(7+h)c{m}^2$
$\therefore 44(7+h)=880\Rightarrow (7+h)=20\Rightarrow h=(20-7)=13$
Hence, the height of the cylinder is $13cm$
Volume of the cylinder $=\left(\pi r^{2}h\right)$ cubic units
$=(\frac{22}{7}\times 7\times 7\times 13)c{m}^3=2002c{m}^3$
Hence, the volume of the cylinder is $2002c{m}^3$

Ek right circular cone ne jitna space occupie kiya hai wo uska volume kehlata hai. The volume of the right circular cone is equal to one-third of the product of the area of the circular base and its height. Jaisa ki hum jante hai ki right circular cone three dimensional hai to uski volume bhi three dimensional hogi. The volume of the cone is equal to one-third of the product of the area of the base and its height. The base area of the cone is obtained by multiplying the square of its radius to $\pi .$
Volume of cone $=\frac{1}{3}\pi r^{2}h$
$r=$ radius of the base circle
$h=$ height of the cone.
$=\pi r^{2}h$

The height and the slant height of a cone are $21cm$ and $28cm$ respectively.
Find the volume of the cone.

Volume of cone =$\frac{1}{3}\pi r^{2}h$
slant height=L=$\sqrt{r^2+h^2}$
substituting values we get = $r=\sqrt{343}cm$
volume of cone=$\frac{1}{3}\times \frac{22}{7}\times 343\times 21=7546{\left(cm\right)}^3$

A right triangle $ABC$ with sides $5cm,12cm$ and $13cm$ is revolved about the side $12cm.$
Find the volume of the solid so obtained.

When we revolve a right angle triangle, we get a conical shape.
Please refer to video for the figure of cone.
So, here, height of cone, $h=12cm$
Radius of cone, $r=5cm$
Volume of cone, $V=\frac{1}{3}\pi r^{2}h$
$V=\frac{1}{3}\times \frac{22}{7}\times 5\times 5\times 12=\frac{2200}{7}=314.21c{m}^3$
So, volume of obtained solid will be $314.21c{m}^3$.

The volume of sphere is the capacity it has. Sphere ek three dimensional shape hai. Iske three axes hai $x$ - axis, $y$- axis and $z$ - axis, which defines its shape. Football, Basketball sphere ke example hai.
Sphere ki volume uske diameter par depend karti hai. Jab hum ek circle ko rotate karte hai to sphere ki formation hoti hai. Archimedes’ principle helps us find the volume of a spherical object. It states that when a solid object is engaged in a container filled with water, the volume of the solid object can be obtained. Because the volume of water that flows from the container is equal to the volume of the spherical object. Volume ko cubic units mai measure karte hai (${\in }^3,f{t}^3,c{m}^3,m^3,$ etc ). Make sure ki aapke sare measurements same units ke ho volume nikalne se pehle.
The volume $V$ of a sphere is four-thirds times pi times the radius cubed.
Volume of Sphere = $\frac{4}{3}\pi r^3$

Higher classes mai aap ishe prove karna bhi sikhoge, but is stage par we will just take it as true. Jaisa ki aap sab jante hai ki hemisphere sphere ka half part hai.
Toh guess what ki hemisphere ki volume kya hogi?
Obviously half of the sphere's volume, i.e. $\frac{1}{2}$ of $\frac{4}{3}\pi r^3$ = $\frac{2}{3}\pi r^3$

Find the volume of a sphere whose surface area is $154$ $c{m}^2$

Here, we are given, the surface area of the sphere is $154c{m}^2$
So, $4\pi r^2=154c{m}^2$
$4\times \frac{22}{7}\times r^2=154c{m}^2$
$r^2=\frac{49}{4}\Rightarrow r=\frac{7}{2}=3.5cm$
So, volume of sphere, $V=\frac{4}{3}\pi r^3=\frac{4}{3}\times \frac{22}{7}\times 3.5\times 3.5\times 3.5$
$V=179.67m^3$

A hemispherical bowl has a radius of $3.5cm.$ What would be the volume of water it would contain?

Volume of hemispherical bowl=$\frac{2}{3}\times \pi \times r^3$
given $r=3.5cm$
volume of water it can contain$=\frac{2}{3}\times \pi \times {\left(3.5\right)}^3=179.66{\left(cm\right)}^3$

In this chapter, you have studied the following formulas :-

1. Surface area of a cuboid $=2(lb+bh+hl)$
2. Surface area of a cube $=6a^2$
3. Curved surface area of a cylinder $=2\pi rh$
4. Total surface area of a cylinder $=2\pi r(r+h)$
5. Curved surface area of a cone $=\pi rl$
6. Total surface area of a right circular cone $=\pi rl+\pi r^2$ or $\pi r(l+r)$
7. Surface area of a sphere of radius $r=4\pi r^2$
8. Curved surface area of a hemisphere $=2{\pi }^2$
9. Total surface area of a hemisphere $=3\pi r^2$
10. Volume of a cuboid $=l\times b\times h$
11. Volume of a cube $=a^3$
12. Volume of a cylinder $=\pi r^{2}h$
13. Volume of a cone $=\frac{1}{3}\pi r^{2}h$
14. Volume of a sphere of radius $r=\frac{4}{3}\pi r^3$
15. Volume of a hemisphere $=\frac{2}{3}\pi r^3$