गुरुत्वाकर्षण कक्षा 9 भौतिकी

भूमिका

इस अध्याय में हम गुरुत्वाकर्षण तथा गुरुत्वाकर्षण के सार्वत्रिक नियम के बारे में अध्ययन करेंगे। हम पृथ्वी पर गुरुत्वाकर्षण बल के प्रभाव के अंतर्गत वस्तुओं की गति पर विचार करेंगे। हम अध्ययन करेंगे कि किसी वस्तु का भार एक स्थान से दूसरे स्थान पर किस प्रकार परिवर्तित होता है। द्रवों में वस्तुओं के प्लवन की शर्तों के बारे में भी हम विचार-विमर्श करेंगे।

गुरुत्वाकर्षण :-

हम जानते हैं कि चंद्रमा पृथ्वी का चक्कर लगाता है, किसी वस्तु को जब ऊपर की ओर फेंकते हैं, तो वह कुछ ऊँचाई तक ऊपर पहुँचती है और फिर नीचे की ओर गिरने लगती है। कहते हैं कि जब न्यूटन एक पेड़ के नीचे बैठे थे तो एक सेब पेड़ से न्यूटन के सिर पर गिरा। अतः तर्क करके हम कह सकते हैं कि सूर्य, ग्रहों तथा हर एक पिंडों के बीच एक बल विद्यमान है। उपरोक्त तथ्यों के आधार पर न्यूटन ने निष्कर्ष निकाला कि केवल पृथ्वी ही सेब और चंद्रमा को आकर्षित नहीं करती, बल्कि विश्व के सभी पिंड एक-दूसरे को आकर्षित करते हैं। वस्तुओं के बीच यह आकर्षण बल गुरुत्वाकर्षण बल कहलाता है। अर्थात-

कणों के बीच कार्य करने वाले पारस्परिक आकर्षण को गुरुत्वाकर्षण (Gravitation) तथा उससे उत्पन्न बल को गुरुत्वाकर्षण बल (Force of Gravitation) कहते है।

गुरुत्वाकर्षण का सार्वत्रिक नियम :-

इस नियम के अनुसार,

न्यूटन ने बताया कि दो पिण्डों के बीच लगने वाले गुरुत्वाकर्षण बल का मान वस्तुओं के द्रव्यमान के गुणनफल के समानुपाती तथा उनके बीच की दूरी के व्युत्क्रमानुपाती होती है।

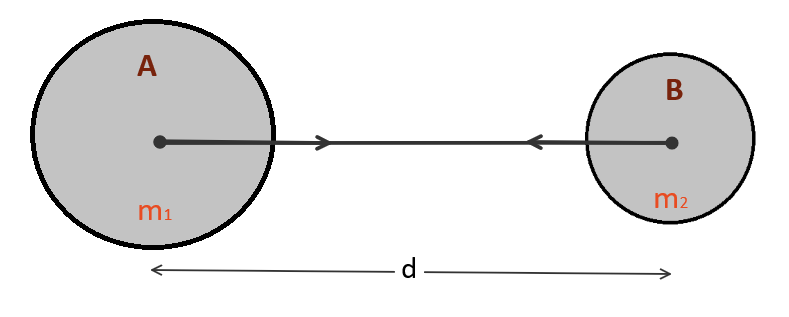
चित्रानुसार माना दो पिंडो के द्रव्यमान क्रमशः

m_{1}

व

m_{2}

है तथा इनके बीच की दूरी

r

तथा इनके बीच लगने वाला बल

F

है तब-

गुरुत्वाकर्षण बल का मान वस्तुओं के द्रव्यमान के गुणनफल के समानुपाती होती है। अर्थात-
$F \propto m_{1} m_{2}$ .......(1)

गुरुत्वाकर्षण बल का मान द्रव्यमानों के बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। अर्थात-
$F \propto \frac{1}{r^{2}}$ .......(2)

समीकरण (1) व समीकरण (2) से-

$F \propto \frac{m_{1} m_{2}}{r^{2}}$

$F = G \frac{m_{1} m_{2}}{r^{2}}$

यहाँ $G$ एक नियतांक है जिसे गुरुत्वीय नियतांक या गुरुत्वाकर्षण नियतांक कहते है।

G

(गुरुत्वीय नियतांक या गुरुत्वाकर्षण नियतांक) का मान $6.67 \times 10^{- 11} \frac{N - M^{2}}{{(K g)}^{2}}$ होता है।

इस पर ताप, दाब आदि का प्रभाव नहीं पड़ता है।

m_{1} = m_{2} = 1 K g

r = 1

$F = G$

जब एकांक द्रव्यमान वाले दो पिण्ड एक दूसरे से एकांक दूरी पर स्थिर हो तो उनके मध्य लगने वाला गुरुत्वाकर्षण बल गुरूत्वीय नियतांक के तुल्य होता है।

गुरुत्वाकर्षण के सार्वत्रिक नियम का महत्व :-

गुरुत्वाकर्षण का सार्वत्रिक नियम अनेक ऐसी परिघटनाओं की सफलतापूर्वक व्याख्या करता है जो सम्बन्धहीन मानी जाती थी :-

हमें पृथ्वी से बाँधे रखने वाला, बल,

पृथ्वी के चारों ओर चंद्रमा की गति,

सूर्य के चारों ओर ग्रहों की गति, तथा

चंद्रमा तथा सूर्य के कारण ज्वार-भाटा।

उदाहरण 1

पृथ्वी का द्रव्यमान $6 \times 10^{24} k g$ है तथा चंद्रमा का द्रव्यमान $7.4 \times 10^{22}$ kg है। यदि पृथ्वी तथा चंद्रमा के बीच की दूरी $3.84 \times 10^{5} k m$ है तो पृथ्वी द्वारा चंद्रमा पर लगाए गए बल का परिकलन कीजिए।
$(G = 6.7 \times 10^{- 11} N m^{2} k g^{- 2}$ )

दिया गया है कि
पृथ्वी का द्रव्यमान $m = 6 \times 10^{24} k g,$
चन्द्रमा का द्रव्यमान $m = 7.4 \times 10^{22} k g,$
पृथ्वी और चन्द्रमा के बीच कि दुरी
$r = 3.84 \times 10^{5} k m = 3.84 \times 10^{5} \times 10^{3} m = 3.84 \times 10^{8} m$
तथा $G = 6.7 \times 10^{- 11} N m^{2} / k g^{2} .$
समीकरण $F = G \frac{M m}{r^{2}}$ से, $F = (6.7 \times 10^{- 11} N m^{2} / k g^{2}) \frac{(6.0 \times 10^{24} k g) \times (7.4 \times 10^{22} k g)}{{(3.84 \times 10^{8} m)}^{2}}$
$= 2.02 \times 10^{20} N,$
अतः पृथ्वी द्वारा चन्द्रमा पर लगाया गया गुरुत्वाकर्षण बल $0.02 \times 10^{20} N$ है।

Learn more

उदाहरण 2

यदि दो लड़के, प्रत्येक का द्रव्यमान 40 kg है, एक-दूसरे से 5.0m दूर बैठे है, तो उनके बीच के गुरुत्वाकर्षण बल का परिणाम ज्ञात करे. $(G = 6.67 \times 10^{- 11} N m^{2} / k g^{2})$

दिया गया है कि
$m_{1} = 40 k g, m_{2} = 40 k g, r = 5.0 m,$
तथा $G = 6.7 \times 10^{- 11} N m^{2} / k g^{2}$
समीकरण $F = G \frac{m_{1} m_{2}}{r^{2}}$ से,
दोनों लड़को के बीच के गुरुत्वाकर्षण बल का परिणाम
$F = \frac{(6.7 \times 10^{- 11} N m^{2} / k g^{2}) (40 k g) (40 k g)}{{(5.0 m)}^{2}}$
$= 429 \times 10^{- 11} N .$

Learn more

उदाहरण 3

चंद्रमा से सूर्य का द्रव्यमान 2.7 करोड़ गुना अधिक होता है और पृथ्वी से चंद्रमा कि दुरी कि तुलन में पृथ्वी से सूर्य की दुरी 390 गुना अधिक होती है. पृथ्वी पर चंद्रमा की अपेक्षा सूर्य का गुरुत्वाकर्षण बल कितना अधिक या कम होगा ?

यदि सूर्य, पृथ्वी और चंद्रमा के द्रव्यमान क्रमशः $M_{s}, M_{e}$ और $M_{m}$ हो तथा पृथ्वी से सूर्य और चंद्रमा की दूरियाँ $r_{s}$ और $r_{m}$ हो, तो पृथ्वी पर सूर्य और चंद्रमा के गुरुत्वकर्षण बल क्रमशः
$F_{s} = G \frac{m_{s} M_{e}}{r_{s}^{2}}$ और $F_{m} = G \frac{M_{m} M_{e}}{r_{m}^{2}}$ होंगे
अतः $\frac{F_{s}}{F_{m}} = \frac{r_{s}^{2}}{G \frac{M_{m} M_{e}}{r_{m}^{2}}} = \frac{M_{s}}{M_{m}} \frac{r_{m}^{2}}{r_{s}^{2}} = \frac{M_{2}}{r_{s}^{2}} {(\frac{r_{m}}{r_{s}})}^{2}$
दिया गया है कि $\frac{M_{s}}{M_{m}} = 2.7 \times 10^{7}$ तथा $\frac{r_{s}}{r_{m}} = 390 .$
$∴ \frac{F_{s}}{F_{m}} = (2.7 \times 10^{7}) {(\frac{1}{390})}^{2} = 178 .$
अतः पृथ्वी पर चंद्रमा की अपेक्षा सूर्य का गुरुत्वाकर्षण बल 178 गुना अधिक होगा|

Learn more

मुक्त पतन :-

हम जानते हैं कि पृथ्वी वस्तुओं को अपनी ओर आकर्षित करती है। पृथ्वी के इस आकर्षण बल को गुरुत्वीय बल कहते हैं।

जब किसी वस्तु को ऊपर की ओर फेंका जाता है तब यह एक निश्चित ऊँचाई तक पहुँच कर नीचे की ओर गिरना आरम्भ कर देती है क्योंकि उस पर पृथ्वी का गुरुत्वाकर्षण बल आरोपित होता है।

किसी वस्तु का पृथ्वी के गुरुत्वीय बल के प्रभाव में पतन (गिरना), मुक्त पतन कहलाता है।

मुक्त पतन में, वस्तु के वेग की दिशा में कोई परिवर्तन नहीं होता क्योंकि वह हमेशा पृथ्वी की तरफ गिरती है। लेकिन वस्तु के वेग के परिमाण में परिवर्तन होता है ।

पृथ्वी के गुरुत्वीय बल के कारण वस्तु के वेग में परिवर्तन या त्वरण गुरुत्वीय त्वरण कहलाता है।

इसे

g

से निर्दिष्ट करते हैं।

g

के मात्रक वही हैं जो त्वरण के हैं, अर्थात्

\frac{m}{s^{2}}

गति के दूसरे नियम से हमें ज्ञात है कि बल द्रव्यमान तथा त्वरण का गुणनफल है।

गुरुत्व त्वरण $g$ के मान का परिकलन :-

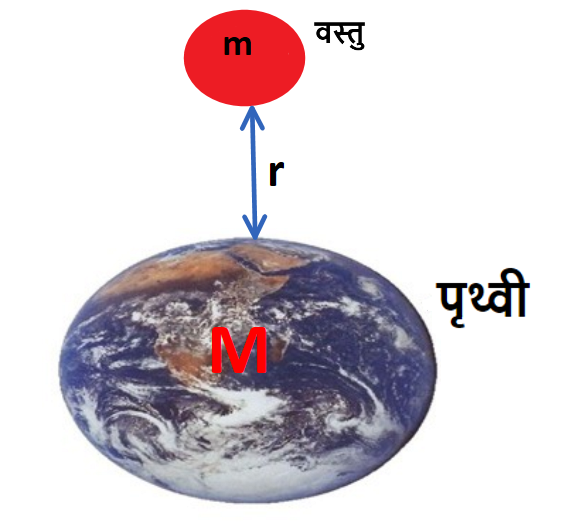
मान लीजिए चित्रानुसार पिंड या वस्तु का द्रव्यमान

m

है। हम पहले से ही जानते हैं कि मुक्त रूप से गिरती वस्तुओं में गुरुत्वीय बल के कारण त्वरण लगता है और इसे

g

से निर्दिष्ट करते हैं। इसलिए गुरुत्वीय बल का परिमाण

F

द्रव्यमान

m

तथा गुरुत्वीय त्वरण

g

के गुणनफल के बराबर होगा, अर्थात्

$F = m g$ ......(1)

हम जानते है कि,

$F = G \frac{m_{1} m_{2}}{r^{2}}$

माना

m_{1}

पृथ्वी का द्रव्यमान है जिसे

M

प्रदर्शित करते है तथा पिंड या वस्तु का द्रव्यमान

m_{2} = m

है तब

$F = G \frac{M m}{r^{2}}$

तब समीकरण (1) से -

$m g = G \frac{M m}{r^{2}}$

या

$g = \frac{G M_{e}}{R_{e}^{2}}$ .......(2)

जहाँ पर

M

पृथ्वी का द्रव्यमान है तथा

R

वस्तु तथा पृथ्वी के बीच की दूरी है।

हम जानते है की गुरुत्वाकर्षण नियतांक का मान

G = 6.6734 \times 10^{- 11} \frac{N m^{2}}{k g^{2}}

होता है, पृथ्वी का द्रव्यमान

M_{e} = 6 \times 10^{24} k g

होता है तथा पृथ्वी की त्रिज्या

R_{e} = 6.4 x 10^{6} m

होता है तब,

$g = \frac{(6.6734 \times 10^{- 11}) \times (6 \times 10^{24})}{(6.4 \times 10^{6})}$

या

$g = 9.8 \frac{m}{s^{2}}$

अतः पृथ्वी का गुरुत्वीय त्वरण पृथ्वी सतह की सतह पर

9.8 \frac{m}{s^{2}}

होता है।

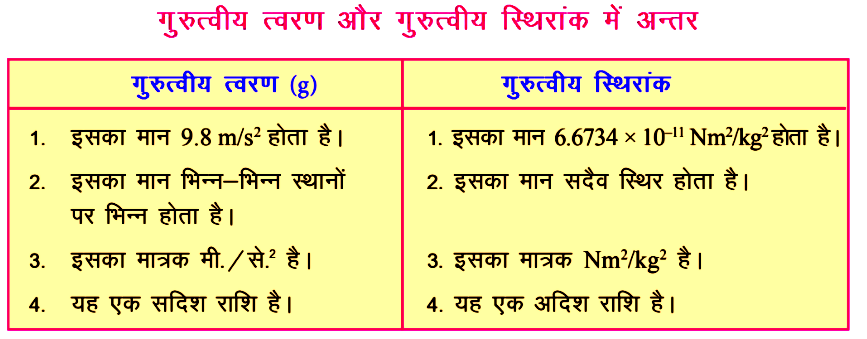
नीचे दिए गए सारणी में गुरुतवै त्वरण तथा गुरुत्वाकर्षण नियतांक के बीच अंतर प्रदर्शित है :-

ocr_image

द्रव्यमान और भार

द्रव्यमान :-

किसी वस्तु में निहित पदार्थ का परिमाण द्रव्यमान कहलाता है या किसी वस्तु के जड़त्व की माप द्रव्यमान कहलाती है।

यह एक अदिश राशि है इसका सिर्फ परिमाण होता है, दिशा नहीं होती है।

SI मात्रक किलोग्राम है जिसे

k g

से प्रदर्शित किया जाता है।

किसी वस्तु का द्रव्यमान सर्वत्र समान रहता है।

द्रव्यमान को

m

से दर्शाया जाता है।

किसी स्थान पर द्रव्यमान (किसी वस्तु का) शून्य नहीं होता है।

भार :-

किसी वस्तु का भार वह बल है जिससे पृथ्वी उसे अपनी ओर आकर्षित करती है।

हम जानते हैं कि

\times

या

F = m \times a

पृथ्वी के गुरुत्वीय बल के कारण त्वरण गुरुत्वीय त्वरण 'g' है।

F = m \times g

लेकिन पृथ्वी द्वारा आरोपित बल भार (weight) कहलाता है। इसे 'W'से प्रदर्शित करते हैं।

W = m \times g

अतः भार एक बल है और उसका S.I मात्रक न्यूटन N है।

एक किलो भार को परिभाषित कीजिए व इसका न्यूटन से सम्बन्ध :-

हम जानते हैं कि

W = m \times g

अगर द्रव्यमान

(m) = 1 k g

तथा

g = 9.8 \frac{m}{s^{2}}

तब

$W = 1 k g \times 9.8 \frac{m}{s^{2}}$

या

$W = 9.8 N$

अतः पृथ्वी का वह गुरुत्वीय बल जो $1$ किलोग्राम द्रव्यमान वाली वस्तु पर लगता है, एक किलोभार कहलाता है जो $9.8 N$ के बराबर है।

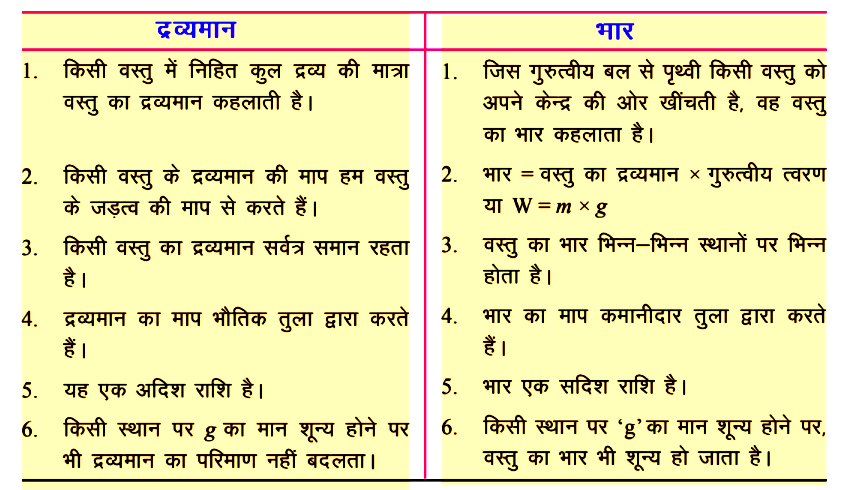
नीचे दिए गए सारणी में द्रव्यमान तथा भार में अंतर प्रदर्शित है :-

ocr_image

चन्द्रमा पर किसी वस्तु का भार

माना किसी वस्तु का द्रव्यमान $m$ है।

पृथ्वी पर उसका भार अर्थात् वह बल जिससे पृथ्वी उसे अपनी ओर खींचती है, वह बल होगा :-

$F_{e} = \frac{G M_{e} m}{R_{e}^{2}}$ .....(1)

जहाँ

M_{e}

= पृथ्वी का द्रव्यमान,

R_{e}

= पृथ्वी की त्रिज्या

चन्द्रमा पर वस्तु का भार

$F_{m} = \frac{G M_{m} m}{R_{m}^{2}}$ ......(2)

जहाँ

M_{m}

= चन्द्रमा का द्रव्यमान,

R_{m}

= चन्द्रमा की त्रिज्या,

समीकरण (2) को समीकरण (1) से भाग देने पर

$\frac{F_{m}}{F_{e}} = ⎡ ⎢ ⎢ ⎣ \frac{\frac{G M_{m} m}{R_{m}^{2}}}{\frac{G M_{e} m}{R_{e}^{2}}} ⎤ ⎥ ⎥ ⎦$

या

$\frac{F_{m}}{F_{e}} = {\frac{G M_{m} m}{R_{m}^{2}}} \times {\frac{R_{e}^{2}}{G M_{e} m}}$

या

$\frac{F_{m}}{F_{2}} = \frac{M_{m}}{M_{e}} \times {(\frac{R_{e}}{R_{m}})}^{2}$

यहाँ

M_{e} = 100 M_{m}

(चन्द्रमा से पृथ्वी का द्रव्यमान लगभग 100 गुना है)

R_{e} = 4 R_{m}

(चन्द्रमा से पृथ्वी की त्रिज्या लगभग 4 गुना है) अतः

$\frac{F_{m}}{F_{e}} = \frac{M_{m}}{100 M_{m}} \times {(\frac{4 R_{m}}{R_{m}})}^{2}$

या

$\frac{F_{m}}{F_{e}} = \frac{16}{100}$

या

$\frac{F_{m}}{F_{e}} = \frac{1}{6}$

या

$F_{m} = \frac{F_{e}}{6}$

अतः चन्द्रमा पर किसी वस्तु का भार उसके पृथ्वी के भार का

\frac{1}{6}

गुना है या पृथ्वी पर किसी वस्तु का भार चन्द्रमा पर उसी वस्तु के भार का

6

गुना है। (ध्यान रहे वस्तु का द्रव्यमान पृथ्वी पर वस्तु के द्रव्यमान के बराबर ही होता है केवल भार में अन्तर होता है।)

उदाहरण 4

एक कार किसी कगार से गिर कर $0.5 s$ में धरती पर आ गिरती हैं परिकलन में सरलता के लिए $g$ का मान $10 m s^{- 2}$ लीजिए।
(i) धरती पर टकराते समय कार की चाल क्या होगी?
(ii) $0.5 s$ के दौरान इसकी औसत चाल क्या होगी?
(iii) धरती से कगार कितनी ऊंचाई पर है?

समय, $t = 0.5 s$
प्रारंभिक वेग, $u = 0 m s^{- 1}$
गुरूत्वीय त्वरण, $g = 10 m s^{- 2}$
कार का त्वरण, $a = + 10 m s^{- 2}$ (अधोमुखी)
(i)चाल $v = a t$
$v = 10 m s^{- 2} \times 0.5 s$
$= 5 m s^{- 1}$
(ii)औसत चाल $= \frac{u + v}{2}$
$= \frac{0 m s^{- 1} + 5 m s^{- 1}}{2}$
$= 2.5 m s^{- 1}$
(iii) तय की गई दूरी, $s = \frac{1}{2} a t^{2}$
$= \frac{1}{2} \times 10 m s^{- 2} \times {(0.5 s)}^{2}$
$= \frac{1}{2} \times 10 m s^{- 2} \times 0.25 s^{2}$
$= 1.25 m$
अतः,
(i) धरती पर टकराते समय इसकी चाल $= 5 m s^{- 1}$
(ii) 0.5 सेकंड के दौरान इसकी औसत चाल $= 2.5 m s^{- 1}$
(iii) धरती से कगार की ऊंचाई $= 1.25 m$

Learn more

उदाहरण 5

एक वस्तु को ऊर्ध्वाधर दिशा में ऊपर की ओर फेंका जाता है और यह $10 m$ की ऊंचाई तक पहुंचती हैं परिकलन कीजिए
(i) वस्तु कितने वेग से ऊपर फेंकी गई तथा
(ii) वस्तु द्वारा उच्चतम बिंदु तक पहुंचने में‌ लिया गया समय।

तय की गयी दुरी s =10 मी
अंतिम वेग v =0 मी से $^{- 1}$
गुरुत्वीय त्वरण g =9 .8 मी से $^{- 2}$
गेंद का त्वरण $a = - 9.8$ मी से $^{- 2}$ (ऊपर की ओर)
$(a) v^{2} - u^{2} = 2 a s$
$0 - u^{2} = 2 \times (- 9.8) \times 10$
$- u^{2} = - 2 \times 9.8 \times 10$
$u = \sqrt{196} = 14$ मी से $^{- 1}$
$(b) v = u + a t$
$0 = 14 - 9.8 \times t$
$t = \frac{14}{9.8} = \frac{10}{7} = 1.43$ से.

Learn more

उदाहरण 6

एक वस्तु का द्रव्यमान $10 k g$ है। पृथ्वी पर इसका भार कितना होगा?

दिया गया है कि वस्तु का द्रव्यमान $m = 10 k g,$ गुरुत्वीय त्वरण $g = 9.8 m / s^{2}$ (मान लिया) .सूत्र $w = m g$ से,
$w = (10 k g) (9.8 m / s^{2}) = 98 k g m / s^{2} = 98 N .$

Learn more

उदाहरण 7

एक वस्तु का भार पृथ्वी की सतह पर मापने पर $10 N$ आता है। इसका भार चंद्रमा की सतह पर मापने पर कितना होगा?

हम जानते है कि
चंद्रमा पर किसी वास्तु का भार $= \frac{1}{6} \times$ पृथ्वी पर उस वस्तु का भार $= \frac{1}{6} \times 10 N = 1.67 N .$

Learn more

प्रणोद तथा दाब :-

प्रणोद :-

किसी वस्तु की सतह के लम्बवत लगने वाले बल को प्रणोद कहते हैं।

या,

एक विशेष दिशा में लगने वाले नेट बल को प्रणोद कहते हैं।

चूँकि प्रणोद एक प्रकार का बल है, अत: प्रणोद का एस आई मात्रक वही है जो बल का एस आई मात्रक है।

अत: प्रणोद [ थ्रस्ट (Thrust)] का एस आई मात्रक न्यूटन (N) है।

दाब :-

प्रति एकांक क्षेत्रफल पर लगने वाले प्रणोद को दाब कहते हैं।

अत:

दाब = प्रणोद/क्षेत्रफल

चूँकि प्रति एकांक क्षेत्रफल पर लगने वाले प्रणोद को दाब कहते हैं, अत: प्रणोद तथा क्षेत्रफल के एस आई मात्रक को दाब की परिभाषा में रखने पर हमें दाब का एस आई मात्रक प्राप्त हो जाता है।

हम जानते हैं कि प्रणोद का एस आई मात्रक न्यूटन (N) है तथा क्षेत्रफल का एस आई मात्रक =

m^{2}

है।

\frac{N}{m^{2}}

वैज्ञानिक ब्लैस पास्कल के सम्मान में, दाब के एस आई मात्रक को पास्कल कहा जाता है। तथा पास्कल को

P_{a}

से व्यक्त किया जाता है।

उत्प्लावकता :-

किसी वस्तु को तरल में आंशिक या पूर्ण रूप से डूबोने पर , तरल द्वारा वस्तु पर एक बल ऊपर की तरफ लगाया जाता है, तरल द्वारा वस्तु पर लगाया गया यह बल ही उत्प्लावन बल या उत्पेक्ष बल कहलाता है।

जब कोई वस्तु किसी तरल में डुबाई जाती है तो वस्तु का भार जो पृथ्वी के गुरुत्वीय बल के कारण वस्तु पर नीचे की ओर व तरल उस पर ऊपर की तरफ बल लगाता है। उत्प्लावन बल सदैव ऊपर की तरफ आरोपित होता है। इस बल का परिमाण द्रव के घनत्व पर निर्भर करता है।

इस बल का मान वस्तु द्वारा हटाये गये तरल के भार या मान पर निर्भर करता है अर्थात कोई वस्तु जितना अधिक तरल को हटाती है उस वस्तु पर लगने वाले उत्प्लावन बल का मान उतना ही अधिक होता है।

वस्तु पर लगने वाला गुरुत्वीय बल > उत्प्लावन बल

निष्कर्ष :- वस्तु डूब जायेगी।

वस्तु पर लगने वाला उत्प्लावन बल > गुरुत्वीय बल

निष्कर्ष :- वस्तु तैरती है।

उत्प्लावन बल का उदाहरण :-

जब किसी गहरे जल में आपका कोई सामान गिर जाता है और आप उसे लेने के लिए निचे की तरफ जाते है तो आप अनुभव करते है कि आपको ऊपर की तरफ धकेला जाता है अर्थात आपको द्रव की सतह पर लाने के लिए आपके ऊपर द्रव द्वारा एक बल कार्य करता है इसी बल को उत्प्लावन बल कहते है, जो द्रव में डुबोने पर उसके ऊपर की तरफ लगता है।

जब आप किसी गुब्बारे को पानी में डुबाने का प्रयास करते है तो आप देखते है कि आपको इसे पानी में डुबोने के लिए बहुत अधिक बल लगाना पड़ता है क्यूंकि आप अनुभव करते है की द्रव एक बल लगाता है जो इसे ऊपर की तरफ धकेलता है, इसी बल को उत्प्लावन बल कहते है।

आर्किमिडीज का सिद्धान्त

आर्किमिडीज का सिद्धान्त के अनुसार :-

जब किसी वस्तु को किसी तरल में पूर्णतः या अंशतः डुबोया जाता है, तब वस्तु ऊपर की तरफ लगने वाले एक बल का अनुभव करती है, यह बल वस्तु द्वारा विस्थापित तरल के भार के बराबर होता है।

आर्किमिडीज के सिद्धान्त के उपयोग :-

यह पदार्थों का आपेक्षिक घनत्व ज्ञात करने में उपयोगी है।

यह जलयानों और पनडुबियों के डिजाइन बनाने में प्रयोग किया जाता है।

दुग्धमापी और हाइड्रोमीटर आर्किमिडीज के सिद्धान्त पर आधारित है।

इसी कारण से लोहे एवं स्टील का बना एक जलयान इतना बड़ा होते हुए भी जल पर तैरता है, लेकिन एक छोटी सी पिन जल में डूब जाती है।

आपेक्षिक घनत्व :-

किसी वस्तु का घनत्व, उसके प्रति एकांक आयतन के द्रव्यमान को कहते हैं।

घनत्व का मात्रक किलोग्राम प्रति घन मीटर है। प्राय: किसी पदार्थ के घनत्व को पानी के घनत्व की तुलना में व्यक्त करना सुविधाजनक होता है। अतः

किसी पदार्थ का आपेक्षिक घनत्व उस पदार्थ का घनत्व व पानी के घनत्व का अनुपात है।

अर्थात्

आपेक्षिक घनत्व = किसी पदार्थ का घनत्व/पानी का घनत्व

चूँकि आपेक्षिक घनत्व समान राशियों का एक अनुपात है, अतः इसका कोई मात्रक नहीं होता।

उदाहरण 8

एक लकड़ी का गुटका मेज पर रखा है। लकड़ी के गुटके का द्रव्यमान $5 k g$ है तथा इसकी विमाएं $40 c m \times 20 c m \times 10 c m$ हैं। लकड़ी के टुकड़े द्वारा मेज पर लगने वाले दाब को ज्ञात कीजिए, यदि इसकी निम्नलिखित विमाओं की सतह मेज पर रखी जाती है (a) $20 c m \times 10 c m$ तथा (b) $40 c m 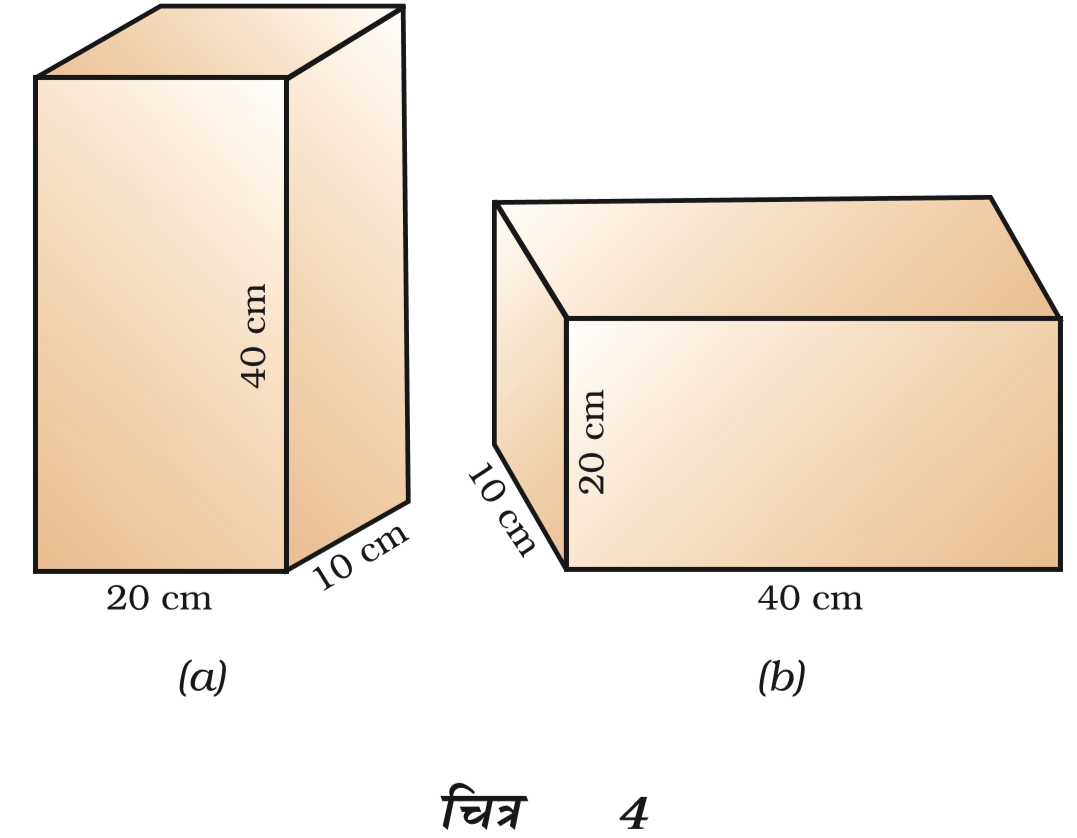\times 20 c m$
ocr_image

लकड़ी के गुटके का द्रव्यमान $= 5 k g$
तथा इसकी विमाएँ $= 40 c m \times 20 c m \times 10 c m$
यहाँ लकड़ी के गुटके का भार मेज की सतह पर प्रणोद लगाता है।
अर्थात्
प्रणोद $= F = m \times g$
$= 5 k g \times 9.8 m s^{- 2}$
$= 49 N$
सतह का क्षेत्रफल $=$ लंबाई $\times$ चौड़ाई
$= 20 c m \times 10 c m$
$= 200 c m^{2} = 0.02 m^{2}$
समीकरण (20) से,
दाब $= \frac{49 N}{0.02 m^{2}}$
$= 2450 N m^{- 2}$
जब गुटके की $40 c m \times 20 c m$ विमाओं की सतह मेज पर रखी जाती है, यह मेज की सतह पर पहले जितना ही प्रणोद लगाता है।
क्षेत्रफल $=$ लंबाई $\times$ चौड़ाई
$= 40 c m \times 20 c m$
$= 800 c m^{2} = 0.08 m^{2}$
समीकरण (20) से,
दाब $= \frac{49 N}{0.08 m^{2}}$
$= 612.5 N m^{- 2}$
सतह $20 c m x 10 c m$ द्वारा लगाया गया दाब $2450 N m^{- 2}$ है तथा सतह $40 c m \times 20 c m$ द्वारा लगाया गया दाब $612.5 N m^{- 2}$ है।

Learn more

उदाहरण 9

चाँदी का आपेक्षिक घनत्व $10.8$ है। पानी का घनत्व $10^{3} k g m^{- 3}$ है। SI मात्रक में चाँदी का घनत्व क्या होगा?

दिया गया है कि
चाँदी का आपेक्षिक घनत्व $= 10.8$
तथा पानी का घनत्व $= 10^{3} k g / m^{3}$
परिभाषा से, चाँदी का आपेक्षिक घनत्व =(चाँदी का घनत्व)/( पानी का घनत्व)
अतः चाँदी का घनत्व
= चाँदी का आपेक्षिक घनत्व x पानी का घनत्व $= 10.8 \times 10^{3} k g / m^{3} .$

Learn more

उदाहरण 10

500 g के एक गुटके का आयतन $350 c m^{3}$ है. यह गुटका $1 g / c m^{3}$ घनत्व वाले पानी में डूबेगा कि तैरेगा? इस गुटके द्वारा विस्थापित पानी का द्रव्यमान कितना होगा ?

दिया गया है कि
गुटके का द्रव्यमान $m = 500 g$
गुटके का आयतन $V = 350 c m^{3} .$
अतः, गुटके के पदार्थ का घनत्व $= \frac{500 g}{350 c m^{3}} = 1.4 g / c m^{3} .$
चूँकि, गुटके के पदार्थ का घनत्व $(1.4 g / c m^{3})$ पानी के घनत्व $(1 g / c m^{3})$ से अधिक है, अतः गुटका पानी में डूब जाएगा. गुटके द्वारा विस्थपित पानी का द्रव्यमान = गुटके के आयतन के बराबर द्रव्यमान $= 350 c m^{3}$ पानी का द्रव्यमान $= 350 c m^{3} \times$ पानी का घनत्व $= 350 c m^{3} \times 1 g / c m^{3} = 350 g .$

Learn more

Home
Ask Doubt
Profile

गुरुत्वाकर्षण कक्षा 9 भौतिकी

भूमिका

गुरुत्वाकर्षण :-

गुरुत्वाकर्षण का सार्वत्रिक नियम :-

F∝m1m2 .......(1)

F∝1r2 .......(2)

F∝m1m2r2

F=Gm1m2r2

F=G

गुरुत्वाकर्षण के सार्वत्रिक नियम का महत्व :-

उदाहरण 1

उदाहरण 2

उदाहरण 3

मुक्त पतन :-

गुरुत्व त्वरण g के मान का परिकलन :-

F=mg ......(1)

F=GMmr2

mg=GMmr2

g=GMeR2e .......(2)

g=(6.6734×10−11)×(6×1024)(6.4×106)

g=9.8ms2

द्रव्यमान और भार

द्रव्यमान :-

भार :-

एक किलो भार को परिभाषित कीजिए व इसका न्यूटन से सम्बन्ध :-

W=9.8N

चन्द्रमा पर किसी वस्तु का भार

Fe=GMemR2e .....(1)

Fm=GMmmR2m ......(2)

FmFe=⎡⎢ ⎢⎣GMmmR2mGMemR2e⎤⎥ ⎥⎦

FmFe={GMmmR2m}×{R2eGMem}

FmF2=MmMe×(ReRm)2

FmFe=Mm100Mm×(4RmRm)2

FmFe=16100

FmFe=16

Fm=Fe6

उदाहरण 4

उदाहरण 5

उदाहरण 6

उदाहरण 7

प्रणोद तथा दाब :-

प्रणोद :-

दाब :-

दाब = प्रणोद/क्षेत्रफल

उत्प्लावकता :-

उत्प्लावन बल का उदाहरण :-

आर्किमिडीज का सिद्धान्त

आर्किमिडीज के सिद्धान्त के उपयोग :-

आपेक्षिक घनत्व :-

आपेक्षिक घनत्व = किसी पदार्थ का घनत्व/पानी का घनत्व

उदाहरण 8

उदाहरण 9

उदाहरण 10

$F \propto m_{1} m_{2}$ .......(1)

$F \propto \frac{1}{r^{2}}$ .......(2)

$F \propto \frac{m_{1} m_{2}}{r^{2}}$

$F = G \frac{m_{1} m_{2}}{r^{2}}$

$F = G$

गुरुत्व त्वरण $g$ के मान का परिकलन :-

$F = m g$ ......(1)

$F = G \frac{M m}{r^{2}}$

$m g = G \frac{M m}{r^{2}}$

$g = \frac{G M_{e}}{R_{e}^{2}}$ .......(2)

$g = \frac{(6.6734 \times 10^{- 11}) \times (6 \times 10^{24})}{(6.4 \times 10^{6})}$

$g = 9.8 \frac{m}{s^{2}}$

$W = 9.8 N$

$F_{e} = \frac{G M_{e} m}{R_{e}^{2}}$ .....(1)

$F_{m} = \frac{G M_{m} m}{R_{m}^{2}}$ ......(2)

$\frac{F_{m}}{F_{e}} = ⎡ ⎢ ⎢ ⎣ \frac{\frac{G M_{m} m}{R_{m}^{2}}}{\frac{G M_{e} m}{R_{e}^{2}}} ⎤ ⎥ ⎥ ⎦$

$\frac{F_{m}}{F_{e}} = {\frac{G M_{m} m}{R_{m}^{2}}} \times {\frac{R_{e}^{2}}{G M_{e} m}}$

$\frac{F_{m}}{F_{2}} = \frac{M_{m}}{M_{e}} \times {(\frac{R_{e}}{R_{m}})}^{2}$

$\frac{F_{m}}{F_{e}} = \frac{M_{m}}{100 M_{m}} \times {(\frac{4 R_{m}}{R_{m}})}^{2}$

$\frac{F_{m}}{F_{e}} = \frac{16}{100}$

$\frac{F_{m}}{F_{e}} = \frac{1}{6}$

$F_{m} = \frac{F_{e}}{6}$