गति कक्षा 9 भौतिकी

Table Of Contents

भूमिका

दैनिक जीवन में हम अपने चारों ओर वस्तुओं को गति करते हुए, अर्थात एक स्थान से दूसरे स्थान जाते हुए देख सकते हैं उदाहरणतः सड़क पर कार, ट्रक, मोटर -साइकिल, साइकिल की गति तथा आप स्वयं भी अपने घर से स्कूल जाते हैं या दुकान जाते हैं तो आप एक जगह से दूसरे जगह समय के साथ अपने स्थान में परिवर्तन करते हैं तो यह सब कैसे होता है, इन सभी का अध्ययन इस अध्याय में किया जाएगा, की गति होती क्या है?, कोई वस्तु स्थिर (रुकी हुई) है अथवा गतिशील (गति में) है, इन सब के बारे में व्याख्या किस प्रकार की जा सकती है?, साथ ही साथ गति कितने प्रकार की होती है, इन सभी के बारे में हम यहां पर सीखेंगे।

गति का वर्णन

समय के सापेक्ष किसी वस्तु की स्थिति में परिवर्तन को गति कहते है।

अथवा जब कोई वस्तु समय के साथ अपनी स्थिति परिवर्तित करती है, तब वस्तु गतिक अवस्था में है। तथा जब कोई वस्तु समय के साथ अपनी स्थिति को परिवर्तित नहीं करती है इसका अर्थ है की वस्तु विरामावस्था में है।

आकाश में उड़ती चिड़िया खुले आकाश में कहीं भी गति करती है, उसी प्रकार तालाब में तैरती मछली भी जल में सभी दिशाओ में गति करती है। दिन व रात पृथ्वी के अपने अक्ष पर घूमने के कारण होता है अर्थात 24 घंटे में पृथ्वी अपनी धुरी पर एक चक्कर लगाती है परन्तु हमें इसका आभास नहीं होता जिसका कारण इस अध्याय में अध्ययन करेंगे,इसी तरह से चंद्रमा भी पृथ्वी के चारों ओर घूमता है तथा चंद्रमा पृथ्वी का एक पूर्ण चक्कर लगभग 28 दिनों में लगा लेता है। पृथ्वी सूर्य के चारों ओर 365 दिन में चक्कर लगाती है। अर्थात पृथ्वी में उपस्थित वस्तु और पृथ्वी के बाहर की उपस्थित पिंड भी गति में है।

अर्थात जब कोई वस्तु समय के सापेक्ष अपनी स्थिति में परिवर्तन करता हो तो वह वस्तु गति में है।

निर्देश तंत्र

गति को निर्देश तंत्र के माध्यम से समझ सकते हैं, हम किसी वस्तु की स्थिति को एक निर्देश बिंदु निर्धारित कर व्यक्त करते हैं। उदाहरार्थ मेले में झूला झूलने की स्थिति की परिकल्पना करे तो उसी झूले में साथ में झूल रहे किसी अन्य व्यक्ति को देखने पर वह स्थिर दिखाई देता है, परन्तु उसी क्षण किसी झूला ना झूल रहे व्यक्ति के द्वारा देखने पर झूला झूल रहे दोनों व्यक्ति गतिमान दिखाई देंगे।

ऐसा इसलिए होता है क्योंकि झूला झूल रहे दोनों व्यक्तियों के एक दूसरे के सापेक्ष स्थिति में परिवर्तन नहीं हो रहा है अपितु ऐसा व्यक्ति जो झूले में उपस्थित नहीं है, उनके सापेक्ष झूला झूलने वाले दोनों व्यक्ति की स्थिति में समय के सापेक्ष लगातार परिवर्तन हो रहे हैं। ऐसी स्थिति में झूले में उपस्थित व्यक्तियों के लिए झूला एक निर्देश तंत्र की तरह कार्य करेगा। तथा उसी निर्देश तंत्र अर्थात झूले में उपस्थित व्यक्ति किसी अन्य व्यक्ति को इस प्रकार देखेगा कि अन्य व्यक्ति भी उसी निर्देश तंत्र में स्थित है। किंतु झूले के बाहर स्थित व्यक्ति का निर्देश तंत्र झूला नहीं होगा अपितु उसकी स्थिति के अनुसार होगा तथा उसके सापेक्ष झूले पर उपस्थित व्यक्ति गतिमान अवस्था पर होंगे।

सरल रेखीय गति

गति का सबसे साधारण प्रकार सरल रेखीय गति है। जब कोई वस्तु एक सीधी रेखा के अनुदिश गति करती है तो उसे सरल रेखीय गति कहते हैं।

दुरी तथा विस्थापन

दुरी

गतिमान वस्तु द्वारा किसी समय पर एक स्थान से दूसरे स्थान तक तय की गई कुल लंबाई को उसकी वस्तु द्वारा तय की गई दूरी कहते हैं।

दूरी को प्रदर्शित करने के लिए दिशा अनिवार्य नहीं होती। दुरी में केवल परिमाण (आंकिक मान) होता है।
इसका मात्रक मीटर होता है |
यह सदैव धनात्मक होती है।

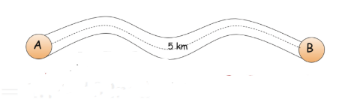
उपर्युक्त चित्र में दो बिंदु A और B के बिच एक रास्ता है। यदि कोई व्यक्ति इस रास्तें से जाता है। तो उसे A बिंदु से B बिंदु तक पहुचने के लिए 5 km की दूरी तय करनी पड़ती है। अतः बिंदु A से बिंदु B के बीच की दूरी 5 km है|

दूरी के पैमाने :-

9.46 \times 10^{16}

10^{- 6}

10^{- 10}

10^{- 15}

विस्थापन :-

किसी वस्तु की एक निश्चित दिशा में प्रारंभिक एवं अंतिम स्थितियों के बीच की न्यूनतम दूरी को विस्थापन कहते हैं। अर्थात किसी वस्तु द्वारा प्रारंभिक और अंतिम बिन्दुओ में मध्य चली गयी सबसे कम दूरी को विस्थापन कहते है। विस्थापन एक सदिश राशि है। अर्थात इसमें परिमाण (आंकिक मान) और दिशा दोनों होती है।

विस्थापन का SI मात्रक मीटर होता है।
विस्थापन एक प्रकार की दूरी ही है। अतः दूरी के सभी मात्रक विस्थापन के मात्रक है।
यह धनात्मक,ऋणात्मक तथा शून्य भी हो सकता है।

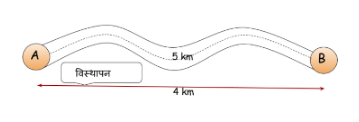
उपर्युक्त चित्र में दो बिंदु A और B के बिच एक रास्ता है| यदि कोई व्यक्ति इस रास्तें से जाता है| तो उसे A बिंदु से B बिंदु तक पहुचने के लिए 5 km की दूरी तय करनी पड़ती है| लेकिन वास्तव में A बिंदु से B बिंदु तक पहुचने के लिए 4 km का रास्ता तय करना पड़ेगा| बिंदु A से बिंदु B तक की न्यूनतम लम्बाई 4 km है। अतः बिंदु A से बिंदु B के बीच का विस्थापन 4 km है। तथा दूरी 5 km है।

चाल तथा औसत चाल

किसी वस्तु द्वारा तय की गई दूरी तथा उस दूरी को तय करने में लगे समय के अनुपात को चाल कहते हैं या किसी वस्तु द्वारा एकांक समय में चली गयी दूरी को चाल कहते है। इसका मात्रक मीटर प्रति सेकंड होता है।

चाल में केवल परिमाण होता है दिशा नहीं होती।
चाल सदैव धनात्मक होता है।

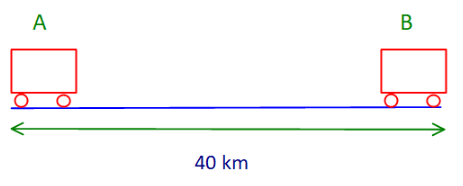
उपर्युक्त दिए गए चित्रानुसार बिंदु A से बिंदु B तक की दुरी 40 किमी दी गई है तो अगर कोई गाडी बिंदु A से बिंदु B तक 1 घंटे में पहुँचती है तो गाड़ी की चाल 40 किमी/घंटे होगी।

ocr_image

किसी दी गई निश्चित दूरी को तय करने के लिए अलग-अलग वस्तुएँ अलग-अलग समय लेंगी। इनमें से कुछ तेज चलती हैं तो कुछ धीमे। वस्तुओं की गति करने की दर अलग अलग हो सकती है। अलग अलग वस्तुएँ समान दर से भी गति कर सकती हैं।

वस्तु द्वारा इकाई समय में तय की गई दूरी के उपयोग से उस वस्तु की गति की दर प्राप्त की जा सकती है। इस राशि को चाल कहा जाता है। चाल का मात्रक मीटर प्रति सेकंड है।

किसी वस्तु की औसत चाल तय की गई कुल दूरी को उस कुल दूरी तय करने में व्यतीत हुए कुल समय से विभाजित करके प्राप्त की जाती है।

औसत चाल = कुल यात्रा की दुरी / कुल लिया गया समय

यदि कोई वस्तु t समय में s दूरी की यात्रा करती है तो उसकी चाल v है -

$v = \frac{s}{t}$

उदाहरण 1

वस्तु 16m की दूरी 4s में तय करती है तथा पुनः 16m की दूरी 2s में तय करती है। वस्तु की औसत चाल क्या होगी?

वस्तु द्वारा कुल तय की गई दूरी =
16 m + 16 m = 32 m
कुल समय = 4 s + 2 s = 6 s
औसत चाल = (कुल तय की गई दूरी)/(कुल लगा हुआ समय)
$= \frac{32 m}{6 s} = 5.33 m s^{- 1}$
इसलिए, वस्तु की औसत चाल $5.33 m s^{- 1}$ होगी।

उदाहरण 2

यात्रा शुरू होते समय कार का ओडोमीटर 2000 km प्रदर्शित करता है और यात्रा समाप्ति पर 2400 km प्रदर्शित करता है। यदि इस यात्रा में $8 h$ लगते हैं, तो कार की औसत चाल को km $h^{- 1}$ और $m s^{- 1}$ में ज्ञात करें।

कार के द्वारा तय की गई दूरी,
s = 2400 km – 2000 km = 400 km
कुल समय, t = 8 h
कार की औसत चाल,
$v_{a v} = \frac{s}{t} = \frac{400 k m}{8 h}$
$= 50 K m h^{- 1}$
$= 50 \frac{k m}{h} \times \frac{1000 m}{1 k m} \times \frac{1 h}{3600 s}$
$= 13.9 m s^{- 1}$
कार की औसत चाल $50 k m h^{- 1}$ or $13.9 m s^{- 1}$ है।

वेग तथा औसत वेग

किसी वस्तु के विस्थापन की दर को या एक निश्चित दिशा में प्रति सेकंड वस्तु द्वारा तय की दूरी को वेग कहते हैं। इसका S.I. मात्रक मी./से. है।

किसी निश्चित दिशा में एकांक समय में वस्तु द्वारा तय की गई दूरी को वस्तु का वेग कहते हैं।

वेग में दिशा तथा परिमाण दोनों होता है।
वेग धनात्मक, ऋणात्मक तथा शून्य हो सकता है।

सूत्र :-

वेग = विस्थापन/समय

यदि वेग को v, विस्थापन को s से तथा समय को t से प्रदर्शित करे तो वेग का सूत्र होगा -

$v = \frac{s}{t}$

उदाहरण

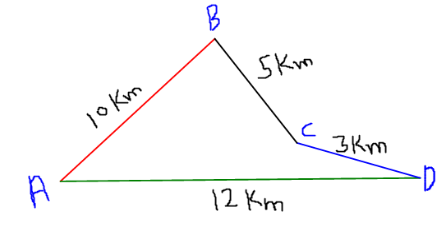
ऊपर दिए चित्रानुसार A से B की दुरी 10 किमी, B से C की दुरी 5 किमी तथा C से D की दुरी 3 किमी दी हुयी है।
यदि कोई व्यक्ति बिंदु A से B तक की दुरी 1 घंटा, B से C तक की दुरी 1 घंटा तथा C से D तक की दुरी 1 घंटा में तय करता है तब व्यक्ति की चाल

A से B तक 10 किमी/घंटा होगी
B से C तक की चाल 5 किमी/घंटा होगी तथा
C से B तक की दुरी 3 किमी/घंटा होगी।

तथा व्यक्ति द्वारा चली गयी कुल दुरी का औसत चाल चली गयी कुल दुरी तथा कुल दुरी तय करने में लगे समय के अनुपात के बराबर होगा अर्थात-

औसत चाल $= \frac{10 + 5 + 3}{1 + 1 + 1} = \frac{18}{3} = 6$ किमी/घंटा

अर्थात व्यक्ति की औसत चाल 6 किमी/घंटा है।

अब हम व्यक्ति के वेग देखे की वस्तु का वेग क्या था तो हम जाने है वेग के परिभाषा से की वेग वस्तु के विस्थापन की दर के बराबर होता है अर्थात वस्तु द्वारा चली गयी प्रारंभिक स्थिति तथा अंतिम स्थिति के बीच की दुरी तथा प्रारंभिक स्थिति से अंतिम स्थिति तक पहुँचने में लगे समय के अनुपात के बराबर होता है।

हम ऊपर दिए हुए चित्र में देख सकते है की वस्तु के प्रारंभिक स्थित तथा अंतिम स्थित अर्थात A तथा D के बीच की दुरी 12 किमी तथा व्यक्ति द्वारा बिंदु A से बिंदु D तक पहुँचने में लगा समय 3 घंटे है तब व्यक्ति का वेग बिंदु A से D तक होगा -

वेग = विस्थापन/समय $= \frac{12}{3} = 4$ किमी/घंटा

अर्थात व्यक्ति का वेग 4 किमी/घंटा होगा।

कोई व्यक्ति किसी बिंदु से चलना प्रारम्भ कर उसी बिंदु पर लौटकर पुनः लौटकर वापस आ जाता है। उस स्थिति में व्यक्ति द्वारा विस्थापन शून्य हो जायेगा अर्थात वेग भी शून्य हो जायेगा।

औसत वेग

किसी वस्तु का वेग समान या असमान हो सकता है। यह वस्तु की चाल, गति की दिशा या दोनों के परिवर्तन के साथ परिवर्तित हो सकती है। जब एक वस्तु सीधी रेखा में बदलती हुई चाल के साथ गति कर रही है, तो हम इसके गति की दर के परिमाण को औसत वेग के द्वारा व्यक्त कर सकते हैं। इसकी गणना औसत चाल की गणना के समान ही होती है। यदि वस्तु का वेग समान रूप से परिवर्तित हो रहा है, तब दिए गए प्रारंभिक वेग और अंतिम वेग के अंकगणितीय माध्य के द्वारा औसत वेग प्राप्त किया जा सकता है।

औसत वेग = (प्रारंभिक वेग + अंतिम वेग)/2

$v_{a v} = \frac{u + v}{2}$

जहां $v_{a v}$ औसत वेग है, u प्रारंभिक वेग है तथा v वस्तु का अंतिम वेग है।

ocr_image

ऊपर दिए हुए चित्र में देख सकते है की यदि बिंदु A प्रारम्भिक बिंदु पर वस्तु की वेग 6 km/h है तथा बिंदु B अर्थात अंतिम बिंदु पर वस्तु की वेग 8 km/h है तब वस्तु का औसत वेग होगा -

$v_{a v} = \frac{6 + 8}{2} = 7 \frac{k m}{h}$

अर्थात वस्तु की औसत वेग 7 km/h होगी |

उदाहरण 3

ऊषा 90m लंबे तालाब में तैरती है। वह एक सिरे से दूसरे सिरे तक सरल रेखीय पथ पर जाती है तथा वापस आती है। इस दौरान वह कुल 180 m की दूरी 1 मिनट में तय करती है। ऊषा की औसत चाल और औसत वेग को ज्ञात कीजिए।

उषा द्वारा 1 मिनट में तय की गई दूरी = 180 मी.
1 मिनट में उषा का विस्थापन = 0 m
औसत चाल = (तय की गई कुल दूरी) $/$ (लगा हुआ समय)
$= \frac{180 m}{1 min} = \frac{180 m}{1 min} \times \frac{1 min}{60 s}$
औसत वेग = (विस्थापन)/(कुल लगा समय)
$= \frac{0 m}{60 s}$
$= 0 m s^{- 1}$
उषा की औसत चाल 3 $m s^{- 1}$ और औसत वेग 0 $m s^{- 1}$ है।

एक समान गति और असमान गति

माना कि एक वस्तु एक सीधी रेखा पर चल रही है। माना पहले 1 सेकंड में यह 50 m दूसरे सेकंड में 50 m, तीसरे सेकंड में 50 m तथा चौथे सेकंड में 50 m दूरी तय करती है। इस स्थिति में वस्तु प्रत्येक सेकंड में 50 m की दूरी तय करती है, यहां वस्तु समान समयांतराल में समान दूरी तय करती है तो उसकी गति को एक समान गति कहते हैं। इस तरह की गति में समयांतराल छोटा होना चाहिए।

दैनिक जीवन में कई बार साक्षात्कर होता हैं कि वस्तुओं के द्वारा समान समयांतराल में असमान दूरी तय की जाती है। उदाहरण स्वरूप एक व्यक्ति 1 सेकंड में 40 मीटर, दूसरे सेकण्ड में 60 मीटर तथा तीसरे सेकण्ड में 50 मीटर दुरी तय करता है। इस स्थिति में व्यक्ति प्रत्येक सेकण्ड अलग अलग दुरी तय करता है, यहाँ व्यक्ति समान समय में समान दुरी तय नहीं करता है तो व्यक्ति की गति असमान गति है।

महत्वपूर्ण तथ्य

इकाई समय में वस्तु द्वारा यात्रा की गई दूरी किसी वस्तु की गति की दर मापने का एक तरीका है। इस मात्रा को गति के रूप में संदर्भित किया जाता है। चाल की SI मात्रक मीटर प्रति सेकेंड है। यह प्रतीक $m s^{- 1}$ या m/s द्वारा दर्शाया जाता है।

गति की अन्य इकाइयों में सेंटीमीटर प्रति सेकंड ( $c m s^{- 1}$ ) और किलोमीटर प्रति घंटे ( $k m s^{- 1}$ ) शामिल हैं।

किसी वस्तु की गति को निर्दिष्ट करने के लिए, हमें केवल इसकी परिमाण की आवश्यकता होती है। किसी वस्तु की गति स्थिर हो ऐसा आवश्यक नहीं है। ज्यादातर मामलों में, वस्तुओं की गति असमान होती है। इसलिए, हम उनकी औसत गति के संदर्भ में ऐसी वस्तुओं की गति की दर का वर्णन करते हैं।

त्वरण

किसी वस्तु की एकसमान सरल रेखीय गति के दौरान, समय के साथ वेग नियत रहता है। इस अवस्था में किसी भी समय अंतराल में वस्तु के वेग में परिवर्तन शून्य है। यद्यपि असमान गति में वेग समय के साथ परिवर्तित होता है। इसका मान विभिन्न समय पर एवं विभिन्न बिंदुओं पर भिन्न-भिन्न होता है। इस प्रकार, किसी भी समयांतराल पर वस्तु के वेग में परिवर्तन शून्य नहीं होता है।

वस्तु के प्रति इकाई समय में वेग परिवर्तन की माप को त्वरण कहते है।
या वस्तु के प्रारंभिक वेग तथा अंतिम वेग के अंतर तथा वेग में व्यतीत समय के अनुपात को त्वरण कहते है।

सूत्र

त्वरण = (वेग मे परिवर्तन वेग)/(परिवर्तन में लगा कुल समय)

त्वरण = (अंतिम वेग - प्रारंभिक वेग)/समय

यदि प्रारंभिक वेग u हो तथा अंतिम वेग v हो तब त्वरण a होगा -

$a = \frac{v - u}{t}$

त्वरण का मात्रक मीटर प्रति सेकण्ड की घात दो होती है अर्थात $\frac{m}{s^{2}}$
त्वरण एक सदिश राशि है। अर्थात त्वरण में दिशा एवं परिमाण दोनों होता है।
त्वरण धनात्मक, ऋणात्मक तथा शून्य हो सकता है।

मंदन ( ऋणात्मक त्वरण )

यदि वस्तु के गति में गति के विपरीत बल लगाया जाये तो वस्तु के गति में आये ऋणात्मक त्वरण या वस्तु के गति की धीमी होने के दर को मंदन कहते है। इसको हम नीचे दिए हुए चित्र की सहायता से समझ सकते है -

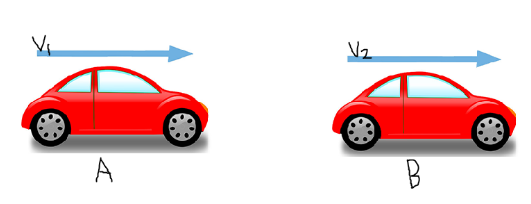
दिए गए चित्र में यदि हम कार का वेग बिंदु A ( प्रारम्भिक स्थिति ) पर

v_{1}

तथा बिंदु B ( अंतिम स्थिति ) पर

v_{2}

हो तब यदि

v_{1}

का मान

v_{2}

से अधिक है अर्थात कार की प्राम्भिक वेग अधिक थी परन्तु अंतिम स्थति पहुंचते पहुंचते कार की अंतिम वेग कम हो गयी गयी तो इस स्थित में कार में ऋणात्मक त्वरण उत्त्पन हुआ जिसकी वजह से कार का वेग कम हो गया तो हम इस ऋणात्मक त्वरण को ही मंदन कहते है।

उदाहरण 4

विरामावस्था से राहुल अपनी साइकिल को चलाना शुरू करता है और 30 s में $6 m s^{- 1}$ का वेग प्राप्त करता है। वह इस प्रकार से ब्रेक लगाता है कि साइकिल का वेग अगले 5 s में कम होकर $4 m s^{- 1}$ हो जाता है। दोनों स्थितियों में साइकिल के त्वरण की गणना करें।

पहली स्थिति में:
प्रारंभिक वेग $u = 0$ ,
अंतिम वेग, $v = 6 m s^{- 1}$ ,
समय, $t = 30 s$
समी. (3) से ,
$a = \frac{v - u}{t}$
उपर्युक्त समीकरण में $v, u$ तथा $t$ का मान रखने पर ,
$a = \frac{(6 m s^{- 1} - 0 m s^{- 1})}{30 s}$
$= 0.2 m s^{- 2}$
दूसरी स्थिति में :
प्रारंभिक वेग , $u = 6 m s^{- 1}$ ,
समय, $t = 5 s$ .
तत्पश्चात , $a = \frac{(4 m s^{- 1} - 6 m s^{- 1})}{5 s}$
$= - 0.4 m s^{- 2}$
पहली स्थिति में साइकिल का त्वरण $0.2 m s^{- 2}$ तथा दूसरी स्थिति में $- 0.4 m s^{- 2}$ है।

गति का ग्राफीय प्रदर्शन

कई घटनाओं के बारे में मूल जानकारी सुविधाजनक विधि से ग्राफ़ द्वारा प्रदर्शित की जा सकती है। किसी वस्तु की गति को दर्शाने के लिए, एक रेखीय ग्राफ़ की आवश्यकता होती है। इस स्थिति में रेखा ग्राफ़ किसी एक भौतिक राशि पर निर्भरता को दर्शाता है जैसे दूरी या वेग की दूसरी राशि, जैसे समय पर निर्भरता।

दूरी-समय ग्राफ

समय के साथ किसी वस्तु की स्थिति परिवर्तन को एक सुविधाजनक पैमाना अपनाकर दूरी-समय ग्राफ़ द्वारा व्यक्त किया जा सकता है। इस ग्राफ़ में समय को X-अक्ष और दूरी को Y-अक्ष पर प्रदर्शित किया जाता है। दूरी-समय ग्राफ़ को विभिन्न अवस्थाओं में प्रदर्शित किया जा सकता है, जैसे वस्तु एकसमान चाल या असमान चाल से गतिशील है, विरामावस्था में है इत्यादि।

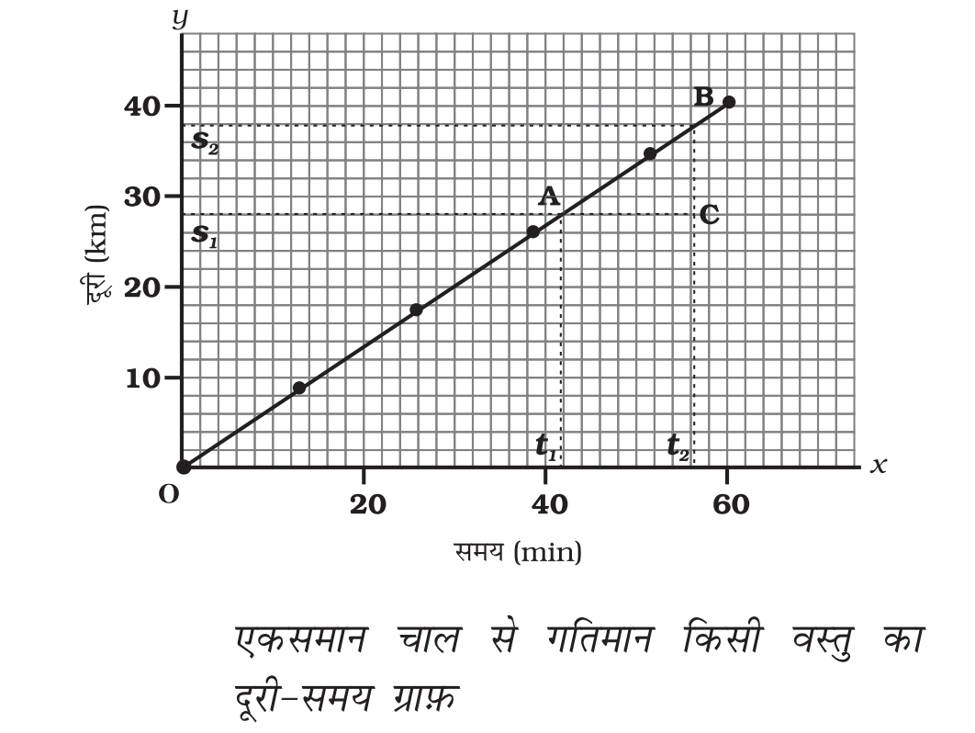
हम जानते हैं कि जब कोई वस्तु समान दूरी समान समयांतराल में तय करती है, तब इसकी चाल एक समान होती है। अत: वस्तु के द्वारा तय की गई दूरी, लिए गए समय के समानुपाती होती है। इस प्रकार एकसमान चाल के लिए, समय के साथ तय की गई दूरी का ग्राफ़ एक सरल रेखा है जैसा कि उपर्युक्त चित्र में प्रदर्शित है।

ग्राफ का OB भाग यह दर्शाता है कि दूरी, एकसमान दर से बढ़ रही है। यदि आप y-अक्ष पर विस्थापन का परिमाण, तय की गई दूरी के बराबर लेते हैं, तो आप एकसमान चाल के स्थान पर एकसमान वेग पद का भी प्रयोग कर सकते हैं। हम दूरी-समय ग्राफ का प्रयोग वस्तु की चाल ज्ञात करने के लिए कर सकते हैं। ऐसा करने के लिए, ऊपर दिए हुए चित्र 1 में दिए गए दूरी समय ग्राफ़ के भाग AB को लें। बिंदु A से x-अक्ष के समांतर एक रेखा तथा बिंदु B से y-अक्ष के समानांतर एक रेखा खींचें। ये दोनों रेखाएँ बिंदु C पर मिलकर एक त्रिभुज ABC बनाती है। अब ग्राफ़ पर, AC समयांतराल (

t_{2} - t_{1}

) को बताता है. जबकि BC दूरी (

S_{2} - S_{1}

) को बताता है। हम ग्राफ़ से देख सकते हैं कि वस्तु A से B बिंदु तक जाने में (

t_{2} - t_{1}

) समय में (

S_{2} - S_{1}

) दूरी तय करती है। अत: वस्तु की चाल निम्न प्रकार से व्यक्त की जा सकती है:

$v = \frac{S_{2} - S_{1}}{t_{2} - t_{1}}$

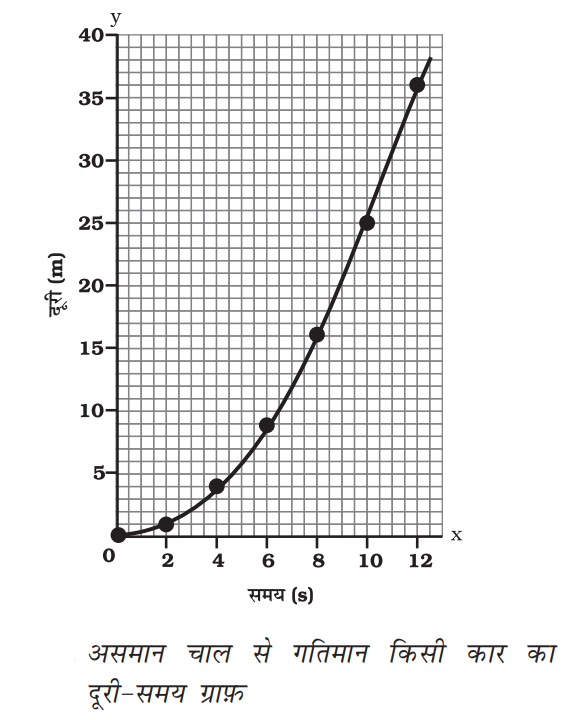
कार की गति के लिए दूरी-समय ग्राफ़ ऊपर दिए हुए चित्र में दर्शाया गया है। ध्यान रहे कि इस ग्राफ की आकृति पहले दर्शाये चित्र में दिए गए ग्राफ़ से भिन्न है। इस ग्राफ़ की प्रकृति समय के साथ कार द्वारा तय की गयी दूरी का आरेखीय परिवर्तन दर्शाता है। इस प्रकार, चित्र में दिखाया गया ग्राफ़ असमान चाल को व्यक्त करता है।

वेग-समय ग्राफ

एक सरल रेखा में चल रही वस्तु के वेग में समय के साथ परिवर्तन को वेग-समय ग्राफ़ द्वारा दर्शाया जा सकता है।

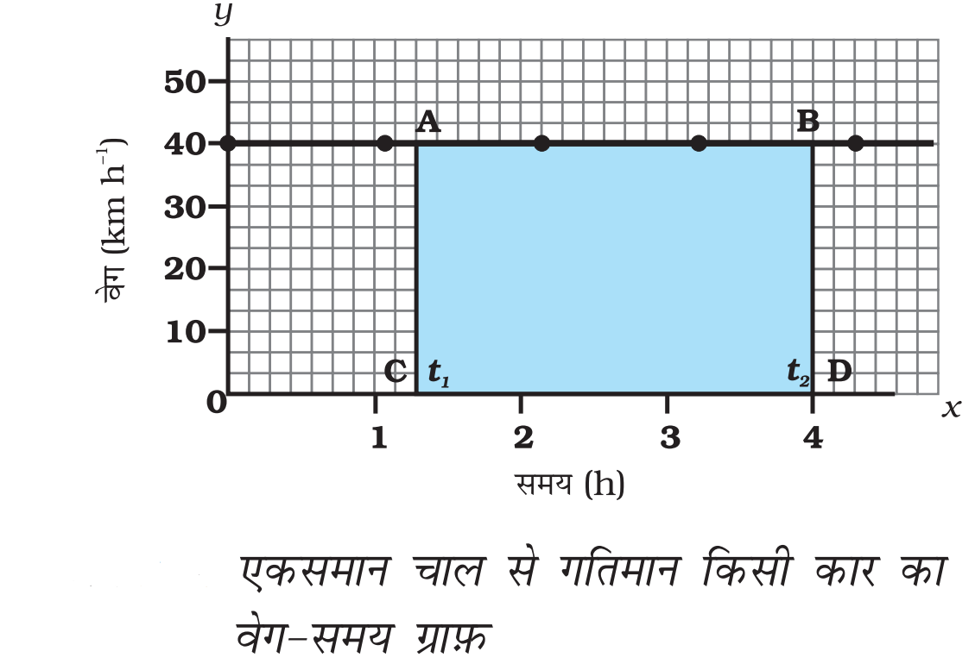
इस ग्राफ में, समय को X-अक्ष पर और वेग को Y-अक्ष पर दर्शाया जाता है। यदि वस्तु एकसमान वेग से गतिमान है, तो समय के साथ वेग-समय ग्राफ़ को ऊंचाई में कोई परिवर्तन नहीं होगा। यह X-अक्ष के समानांतर एक सीधी रेखा होगी। उपर्युक्त चित्र में, एक कार जो कि 40 km/h के एकसमान वेग से गति कर रही है, के वेग समय-ग्राफ़ को दर्शाया गया है।

एकसमान वेग से चल रही किसी वस्तु के वेग तथा समय के गुणनफल से विस्थापन प्राप्त किया जाता है। वेग-समय ग्राफ़ तथा समय अक्ष के द्वारा घेरा गया क्षेत्र विस्थापन के परिमाण के बराबर होता है। उपर्युक्त चित्र से

t_{1}

और

t_{2}

समय के बीच कार द्वारा तय की गई दूरी को ज्ञात करने के लिए समय

t_{1}

व

t_{2}

के संगत बिंदुओं से ग्राफ़ पर लंब खींचें। 40 km/h के वेग को ऊँचाई AC या BD और समय

(t_{2} - t_{1})

को लंबाई AB से प्रदर्शित किया गया है।

इसलिए समय ( $t_{2} - t_{1}$ ) में कार द्वारा तय की गई दूरी को इस प्रकार व्यक्त किया जा सकता है -

$S = A C \times C D$

$S = [(40 \frac{k m}{h}) \times (t_{2} - t_{1}) h]$

$S = 40 (t_{2} - t_{1}) k m$

S = चतुर्भुज ABDC का क्षेत्रफल

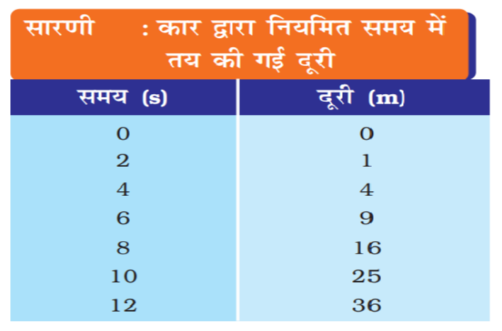
वेग-समय ग्राफ़ के द्वारा एकसमान रूप से त्वरित गति का अध्ययन भी कर सकते हैं। यदि परिकल्पना करें कि एक कार सीधे मार्ग पर चलाया जाता है। माना कि चालक के साथ में बैठा एक व्यक्ति प्रत्येक 5 s के बाद कार के स्पीड मीटर का पाठ्यांक लेता है। कार का वेग विभिन्न समयों पर m/s व km/h में नीचे दी हुयी सारणी में प्रदर्शित किया गया है।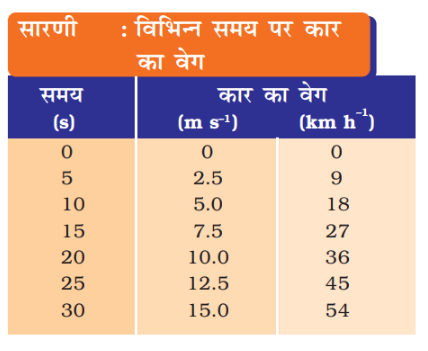

ocr_image

इस स्थिति में कार की गति के लिए समय-वेग ग्राफ़ नीचे दिए चित्र में प्रदर्शित किया गया है। ग्राफ़ की प्रकृति यह प्रदर्शित करती है कि समान समयांतराल में वेग में परिवर्तन समान रूप से होता है। इस प्रकार सभी एकसमान त्वरित गतियों के लिए वेग-समय ग्राफ़ सीधी रेखा है।

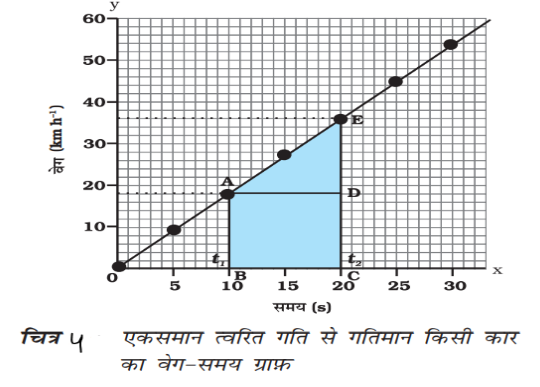
आप कार के द्वारा तय की गई दूरी को वेग-समय ग्राफ़ द्वारा प्राप्त कर सकते हैं। वेग-समय ग्राफ़ का क्षेत्रफल दिए गए समयांतराल में कार द्वारा तय की गई दूरी (विस्थापन के परिमाण) को बताता है यदि कार एकसमान वेग से गति करे, तो ग्राफ़ (उपर्युक्त चित्र) में दर्शाए गए क्षेत्र ABCD द्वारा तय की गई दूरी को दर्शाया जाएगा। चूंकि कार के वेग का परिमाण त्वरण के कारण परिवर्तित हो रहा है, अत: कार के द्वारा तय की गई दूरी S, वेग-समय ग्राफ (उपर्युक्त चित्र) में प्रदर्शित क्षेत्र ABCDE द्वारा व्यक्त की जाएगी।

S = ABCDE का क्षेत्रफल

S = आयत ABCD का क्षेत्रफल + त्रिभुज ADE का क्षेत्रफल

$S = (A B \times B C) + \frac{1}{2} (A D \times D E)$

असमान त्वरित गति की स्थिति में वेग-समय ग्राफ़

असमान त्वरित गति की स्थिति में वेग-समय ग्राफ़ किसी भी आकृति का हो सकता है। नीचे दिया गया प्रथम चित्र (a) वेग-समय ग्राफ़ को दर्शाता है, जो कि एक वस्तु के गति को प्रदर्शित करता है, जिसका वेग समय के साथ घटता है। जबकि नीचे दिए गए द्वितीय चित्र (b) में किसी वस्तु के वेग में असमान परिवर्तन को वेग-समय ग्राफ़ द्वारा दर्शाया गया है।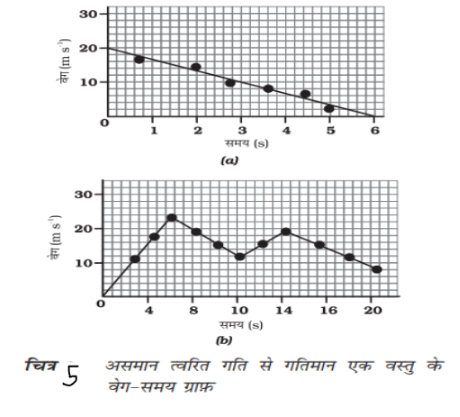

ocr_image

ग्राफीय विधि से गति के समीकरण

कोई वस्तु सीधी रेखा में एकसमान त्वरण से चलती है तो एक निश्चित समयांतराल में समीकरणों के द्वारा उसके वेग, गति के दौरान त्वरण व उसके द्वारा तय की गई दूरी में संबंध स्थापित करना संभव है, जिन्हें गति के समीकरण के नाम से जाना जाता है।

इस प्रकार के तीन समीकरण निम्नलिखित हैं :-

$v = u + a t \dots \dots ... ... (A)$

$s = u t + \frac{1}{2} a t^{2} \dots \dots \dots \dots . . (B)$

$v^{2} = u^{2} + 2 a s \dots \dots \dots \dots . (C)$

जहाँ u वस्तु का प्रारंभिक वेग है जो कि किसी समय के लिये एकसमान त्वरण a से चलती है, व अंतिम वेग v है तथा t समय में वस्तु के द्वारा तय की गई दूरी s है।

समीकरण (A) वेग एवं समय में संबंध व्यक्त करती है तथा समीकरण (B) समय व स्थिति के बीच संबंध व्यक्त करती है। समीकरण (C) जो कि वेग एवं स्थिति के बीच संबध व्यक्त करती है, जिसे समीकरण (A) एवं (B) को व्यक्त कर प्राप्त किया जा सकता है।

इन तीनों समीकरणों को ग्राफ़ीय विधि से भी प्राप्त किया जा सकता है।

वेग-समय संबंध के लिए समीकरण

कोई वस्तु जो कि एकसमान त्वरण के साथ चलती है, उसके वेग समय ग्राफ़ को देखा जाए, जैसा कि नीचे दिए गए चित्र में प्रदर्शित है (ऊपर दिए गए चित्र के समकक्ष, किंतु अब u= 0)। इस ग्राफ़ से आप देख सकते हैं कि वस्तु का प्रारभिक वेग u है (बिंदु A पर) और यह t समय में बढ़कर v (बिंदु B पर) हो जाता है। वेग, एकसमान दर के साथ परिवर्तित होता है।

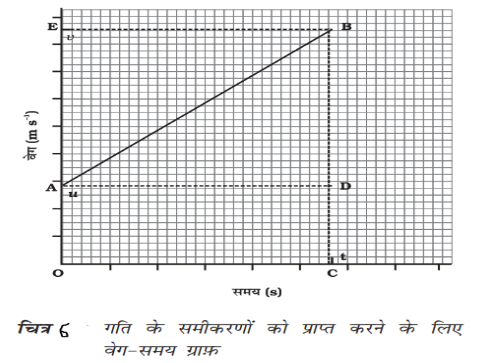
चित्र में, बिंदु B से दो लम्ब BC एवं BE क्रमशः: समय- तथा वेग- अक्षों पर खींचे गए हैं। प्रारंभिक वेग OA के द्वारा, अंतिम वेग BC के द्वारा तथा समयांतराल , OC के द्वारा प्रदर्शित किया गया है। BD = BC - CD समयांतराल 1 में वेग में परिवर्तन को दर्शाता है। अब OC के समानांतर AD रेखा खींचें। ग्राफ़ से हम पाते हैं कि

$B C = B D + D C = B D + O A$

इसमें BC = v और OA = u रखने पर हम पाते हैं -

$v = B D + u$

या,

$B D = v - u \dots \dots \dots \dots . (1)$

वेग समय ग्राफ से ( चित्र 6 ), वस्तु के त्वरण को व्यक्त जाता है -

a = वेग में परिवर्तन/वेग परिवर्तन में लगा समय

$a = \frac{B D}{A D} = \frac{B D}{O C}$

OC = t रखने पर,

$a = \frac{B D}{t}$

$B D = a t$

BD का मान समीकरण 1 में रखने पर -

$a t = v - u$

या

$v = u + a t \dots \dots \dots (A)$

यही समीकरण गति की प्रथम समीकरण है।

समय-स्थिति संबंध के लिए समीकरण

मान लें कि वस्तु द्वारा एकसमान त्वरण a से t समय में s दूरी तय की गयी। उपर्युक्त चित्र में वस्तु के द्वारा तय की गई दूरी, वेग-समय ग्राफ़ AB के नीचे घिरे क्षेत्र OBC द्वारा प्राप्त की जाती है।

इस प्रकार, वस्तु के द्वारा तय की गई दूरी s निम्न प्रकार व्यक्त की जाती है,

s = OABC का क्षेत्रफल (जो एक समलंब है) = आयत ABCD का क्षेत्रफल + त्रिभुज ABD का क्षेत्रफल

$s = (O A \times O C) + \frac{1}{2} (A D \times B D)$

OA = u, OC = AD = t और BD = at, रखने पर ....

$s = u t + \frac{1}{2} t \times a t$

$s = u t + \frac{1}{2} a t^{2} \dots \dots \dots . . (B)$

यही समीकरण गति का द्वितीय समीकरण है।

वेग-स्थिति संबंध के लिए समीकरण

उपर्युक्त दिए गए चित्र में प्रदर्शित वेग-समय ग्राफ़ से, वस्तु के द्वारा एकसमान त्वरण a से t समय में तय की गई दूरी S को ग्राफ़ के नीचे समलंब चतुर्भुज OABC द्वारा घेरे गए क्षेत्रफल द्वारा प्रदर्शित किया गया है। अर्थात्,

$s =$ समलंब OABC का क्षेत्रफल

$s = \frac{(O A + B C) \times O C}{2}$

$s = \frac{(v + u) \times t}{2} \dots \dots \dots (1)$

वेग-समय सम्बन्ध ( समीकरण A ) हम प्राप्त कर सकते है -

$t = \frac{v - u}{a}$

t का मान समीकरण 1 में रखने पर -

$s = \frac{(v + u) \times (v - u)}{2} a$

या

$s = \frac{v^{2} - u^{2}}{2} a$

या

$2 a s = v^{2} - u^{2}$

या

$v^{2} = u^{2} + 2 a s \dots ... ... ... . (C)$

यही समीकरण गति का तृतीय समीकरण है |

उदाहरण 5

एक रेलगाड़ी विरामावस्था से चलना प्रारंभ करती है और 5 मिनट में $72 k m / h$ का वेग प्राप्त कर लेती है । मान लें कि त्वरण एक समान है परिकलन कीजिए (i) त्वरण, (ii) इस वेग को प्राप्त करने के लिए रेलगाड़ी द्वारा तय की गई दूरी।

दिया गया है
$u = 0, v = 72 k m h^{- 1} = 20 m s^{- 1}$ तथा t=5 minutes =300s
(i) समीकरण (5) से हम जानते है कि
$a = \frac{(v - u)}{t}$
$= \frac{20 m s^{- 1} - 0 m s^{- 1}}{300 s}$
$= \frac{1}{15} m s^{- 2}$
(ii) समीकरण (7) से $2 a s = v^{2} - u^{2} = v^{2} - 0$
अतः ,
$s = \frac{v^{2}}{2 a}$
$s = \frac{{(20 m s^{- 1})}^{2}}{2 \times (1 / 15) m s^{- 2}}$
$s = 3000 m$
$s = 3 k m$
रेलगाड़ी का त्वरण $\frac{1}{15} m s^{- 2}$ और तय की गई दूरी $3 k m$ है।

उदाहरण 6

कोई कार एकसमान रूप से त्वरित होकर $5 s$ में $18 k m h^{- 1}$ से $36 k m h^{- 1}$ की गति प्राप्त करती है। ज्ञात करें (i) त्वरण, (ii) उतने समय में कार के द्वारा तय की गई दूरी।

दिया गया है
u=18 $k m h^{- 1} = 5 m s^{- 1}$
$v = 36 k m h^{- 1} = 10 m s^{- 1}$ और
t = 5 s.
(i) समीकरण (5) से
$a = \frac{v - u}{t}$
$= \frac{10 m s^{- 1} - 5 m s^{- 1}}{5 s}$
$= 1 m s^{- 2}$
(ii) समीकरण (6) से
$s = u t + \frac{1}{2} a t^{2}$
$= 5 m s^{- 1} \times 5 s + \frac{1}{2} \times 1 m s^{- 2} \times {(5 s)}^{2}$
$= 25 m + 12.5 m$
=37.5 m
कार का त्वरण 1 $m s^{- 2}$ और तय की गई दूरी 37.5 m. है|

उदाहरण 7

किसी कार पर ब्रेक लगाने पर वह गति के विपरीत दिशा में $6 m s^{- 2}$ का त्वरण उत्पन्न करती है। यदि कार ब्रेक लगाए जाने के बाद रूकने में 2s का समय लेती है तो उतने समय में तय की गई दूरी की गणना करें।

दिया गया है
$a = - 6 m s^{- 2}, t = 2 s$ और $v = 0 m s^{- 1}$
समीकरण
$v = u t + a t$
$0 = u + (- 6 m s^{- 2}) \times 2 s$
or $u = 12 m s^{- 1}$ .
समीकरण (6) से
$s = u t + \frac{1}{2} a t^{2}$
$s = (12 m s^{- 1}) \times (2 s) + \frac{1}{2} (- 6 m s^{- 2}) {(2 s)}^{2}$
$s = 24 m - 12 m$
$s = 12 m$
अतः, ब्रेक लगाने के पश्चात रुकने से पहले कार 12 मीटर की दूरी तय करेगा।

वृत्तीय गति

जब वस्तु के वेग में परिवर्तन होता है तब हम कहते हैं कि वह वस्तु त्वरित हो रही है। वेग में यह परिवर्तन, वेग के परिमाण अथवा गति की दिशा अथवा दोनों के कारण हो सकता है।

यह तभी संभव है जब कोई वस्तु एक बंद पथ पर या एक वृत्तीय मार्ग में गति करे। इस प्रकार की गति में जो कण है वह किसी निश्चित बिन्दु के परित: वृत्तीय पथ पर अचर वेग से गति करता है।

जब कोई पिण्ड ऐसी गति करता है कि उसकी गति का पथ एक वृत्त हो तो ऐसी गति को वृत्तीय गति (Circular motion) कहते है।
जब कोई वस्तु किसी वृत्ताकार मार्ग पर गति करती है तो इसे वस्तु की वृत्तीय गति कहा जाता है।

एकसमान वृत्तीय गति

जब कोई वस्तु एक निश्चित बिन्दु को केन्द्र मानकर उसके चारो ओर वृत्तीय पथ पर समान चाल से गति करती है तो उसकी गति एकसमान वृत्तीय गति कहलाती है।

यदि कोई कार प्रत्येक 10 मिनट में 1 किलोमीटर की दूरी तय करती है, तो इस स्थिति में कार की गति एकसमान गति कहलाती है।
घड़ी की मिनट वाली सूई प्रत्येक एक घंटे में एक चक्कर पूरा करती है। वहीं घड़ी की घंटे वाली सूई प्रत्येक 12 घंटे में एक चक्कर पूरा करती है। तो इस स्थिति में घड़ी के सुई की गति एकसमान वृत्तीय गति कहलाएगी।

वृत्तीय गति के उदहारण

नीचे दिए हुए चित्र के अनुसार यदि कोई व्यक्ति आयताकार पथ ABCD पर एकसमान गति करता है तो बिंदु A से चलने के बाद जब वह बिंदु B पर पहुँचता है तो उसको अपने वेग की दिशा में परिवर्तन करना होगा तभी वह बिंदु B से बिंदु C की तरफ गति कर पायेगा तो यहाँ पर देखा जा सकता है की वस्तु के वेग के परिमाण में बिना परिवर्तन किये उसकी दिशा में परिवर्तन कर दिया गया तथा वेग परिवर्तन की दर को ही त्वरण कहते है इसी प्रकार जब वस्तु बिंदु C से D की तरफ मुड़ेगी तब भी उसके दिशा में परिवर्तन होगा तो इस स्थिति पर ऐसा कह सकते है की वस्तु के वेग के परिमाण बिना बदले ही वस्तु को त्वरित कर दिया। वस्तु की इसी गति को एक सामान वृत्तीय गति कहते है।

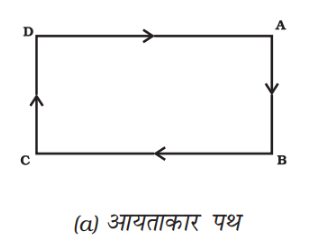
इसी प्रकार अगर कोई वस्तु वृत्तीय मार्ग में एकसमान गति कर रहा है तो उसके दिशा में निरंतर परिवर्तन होता रहेगा अर्थात वस्तु त्वरित हो जाएगी। तो वस्तु के इसी गति को एक सामान वृत्तीय गति कहते है।

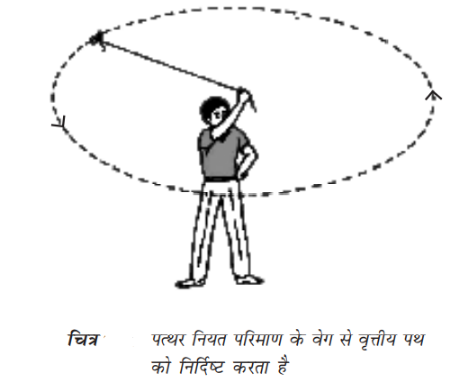
जब कोई व्यक्ति एक पत्थर को डोरी से बाँध कर हवा में घुमाता है तो डोरी से बंधा हुआ पत्थर वृत्तीय मार्ग में गति करता है अर्थात पत्थर की गति वृत्तीय गति होगी।

वस्तुनिष्ठ प्रश्न

Learn more

लघु उत्तरीय प्रश्न

Learn more

दीर्घ उत्तरीय प्रश्न

Learn more

अंकीय प्रश्न

Learn more

QUESTIONS

LEVEL 1

Learn more

LEVEL 2

Learn more

Home
Ask Doubt
Profile

गति कक्षा 9 भौतिकी

भूमिका

गति का वर्णन

निर्देश तंत्र

सरल रेखीय गति

दुरी तथा विस्थापन

दुरी

दूरी के पैमाने :-

विस्थापन :-

चाल तथा औसत चाल

औसत चाल = कुल यात्रा की दुरी / कुल लिया गया समय

v=st

उदाहरण 1

उदाहरण 2

वेग तथा औसत वेग

सूत्र :-

वेग = विस्थापन/समय

v=st

उदाहरण

औसत चाल =10+5+31+1+1=183=6 किमी/घंटा

वेग = विस्थापन/समय =123=4 किमी/घंटा

औसत वेग

औसत वेग = (प्रारंभिक वेग + अंतिम वेग)/2

vav=u+v2

vav=6+82=7kmh

उदाहरण 3

एक समान गति और असमान गति

महत्वपूर्ण तथ्य

त्वरण

सूत्र

त्वरण = (वेग मे परिवर्तन वेग)/(परिवर्तन में लगा कुल समय)

त्वरण = (अंतिम वेग - प्रारंभिक वेग)/समय

a=v−ut

मंदन ( ऋणात्मक त्वरण )

उदाहरण 4

गति का ग्राफीय प्रदर्शन

दूरी-समय ग्राफ

v=S2−S1t2−t1

वेग-समय ग्राफ

S=AC×CD

S=[(40kmh)×(t2−t1)h]

S=40(t2−t1)km

S = चतुर्भुज ABDC का क्षेत्रफल

S = ABCDE का क्षेत्रफल

S = आयत ABCD का क्षेत्रफल + त्रिभुज ADE का क्षेत्रफल

S=(AB×BC)+12(AD×DE)

असमान त्वरित गति की स्थिति में वेग-समय ग्राफ़

ग्राफीय विधि से गति के समीकरण

v=u+at……......(A)

s=ut+12at2…………..(B)

v2=u2+2as………….(C)

वेग-समय संबंध के लिए समीकरण

BC=BD+DC=BD+OA

v=BD+u

BD=v−u………….(1)

a = वेग में परिवर्तन/वेग परिवर्तन में लगा समय

a=BDAD=BDOC

a=BDt

BD=at

at=v−u

v=u+at………(A)

समय-स्थिति संबंध के लिए समीकरण

s = OABC का क्षेत्रफल (जो एक समलंब है) = आयत ABCD का क्षेत्रफल + त्रिभुज ABD का क्षेत्रफल

s=(OA×OC)+12(AD×BD)

s=ut+12t×at

s=ut+12at2………..(B)

वेग-स्थिति संबंध के लिए समीकरण

s= समलंब OABC का क्षेत्रफल

s=(OA+BC)×OC2

s=(v+u)×t2………(1)

t=v−ua

s=(v+u)×(v−u)2a

s=v2−u22a

2as=v2−u2

v2=u2+2as…..........(C)

उदाहरण 5

उदाहरण 6

उदाहरण 7

वृत्तीय गति

एकसमान वृत्तीय गति

$v = \frac{s}{t}$

$v = \frac{s}{t}$

औसत चाल $= \frac{10 + 5 + 3}{1 + 1 + 1} = \frac{18}{3} = 6$ किमी/घंटा

वेग = विस्थापन/समय $= \frac{12}{3} = 4$ किमी/घंटा

$v_{a v} = \frac{u + v}{2}$

$v_{a v} = \frac{6 + 8}{2} = 7 \frac{k m}{h}$

$a = \frac{v - u}{t}$

$v = \frac{S_{2} - S_{1}}{t_{2} - t_{1}}$

$S = A C \times C D$

$S = [(40 \frac{k m}{h}) \times (t_{2} - t_{1}) h]$

$S = 40 (t_{2} - t_{1}) k m$

$S = (A B \times B C) + \frac{1}{2} (A D \times D E)$

$v = u + a t \dots \dots ... ... (A)$

$s = u t + \frac{1}{2} a t^{2} \dots \dots \dots \dots . . (B)$

$v^{2} = u^{2} + 2 a s \dots \dots \dots \dots . (C)$

$B C = B D + D C = B D + O A$

$v = B D + u$

$B D = v - u \dots \dots \dots \dots . (1)$

$a = \frac{B D}{A D} = \frac{B D}{O C}$

$a = \frac{B D}{t}$

$B D = a t$

$a t = v - u$

$v = u + a t \dots \dots \dots (A)$

$s = (O A \times O C) + \frac{1}{2} (A D \times B D)$

$s = u t + \frac{1}{2} t \times a t$

$s = u t + \frac{1}{2} a t^{2} \dots \dots \dots . . (B)$

$s =$ समलंब OABC का क्षेत्रफल

$s = \frac{(O A + B C) \times O C}{2}$

$s = \frac{(v + u) \times t}{2} \dots \dots \dots (1)$

$t = \frac{v - u}{a}$

$s = \frac{(v + u) \times (v - u)}{2} a$

$s = \frac{v^{2} - u^{2}}{2} a$

$2 a s = v^{2} - u^{2}$

$v^{2} = u^{2} + 2 a s \dots ... ... ... . (C)$