FORCE AND LAWS OF MOTION for Class 9 PHYSICS
INTRODUCTION
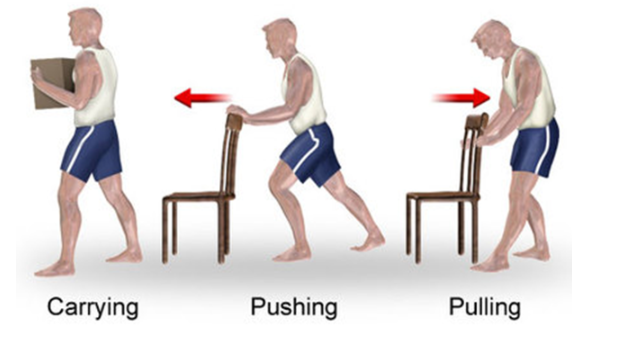
Kisi bhi body (object) ko motion me lane ke liye hum usko push ya pull karte hai. Aur is push or pull ko force kahte hai. Jis direction me body move karti hai use ‘direction of force’ kahte hai. Example, jaise ki hum jab door open ya close karte hai toh hum door ko push karte hai, yaha force hum apne opposite direction me lagate hai, jab hum door ko apni taraf pull karte hai tab isme force hum apni taraf lagate hai.
Force har ek action me lagta hai jaise pushing, pulling, lifting, stretching, twisting and pressing. For example, force use hota hai ja football ko kick karte hai, drawer ko kholne ke liye hum uske handle ko pull karte toh yaha bhi force lagta hai, kisi bhi box ko floor se uthane ke liye bhi force lagta hai.
Har ek object me motion lane ke force lagta hai.
Jab chalti hui car me break lagate hai toh us pr bhi force lagta hai jis se car rest position me aata hai.
- Force kisi stationary (rest) object ko motion me la sakta hai.
- Force ke karan object running position se rest position me aa sakta hai.

EFFECT OF FORCE
Force ko dekha nahi ja sakta. Objects ko observe karke hum yeh pata kr sakte hai hi kaun se type ka force us object me laga hai. Force ke effect’s object pr :
- A force can move stationary objects.
- A force can stop moving object.
- A force can change the speed of a moving body.
- A force can change the direction of a moving body.
- A force can change the size and shape of the body.

Ground me rakhe hue football ko jab hum kick karte hai tab football me movement shuru ho jati hai. Is case me humare leg ka force football ko move karta hai. Is example, se hum yah conclude kr sakte hain ki force stationary object ko move kr sakta hai. Football kuchh der ke baad ruk jata hai kyunki football ground ke force of friction ki wajah se ruk jata hai, aise hi force of break chalti hui car ko rok deta hai. Is example se hum yah conclude karte hain ki force moving body ko stop kr deta hai.
Suppose hum cycle per ek hi speed se chal rahe hain tab koi piche se cycle ko push karen toh cycle ki speed badh jayegi. Ager vahi use cycle ko pull kare to cycle ki speed km ho jayegi. Is example, se hume yah pata chalta hai ki push aur pull ki vajah se cycle ki speed mein change hoti hai.
Ager hum ek light spring le aur isi dono side se pull kare to spring ke shape aur size me changes hoga. The turns in spring became further apart aur iski length increase hogi. Is case me humare hand ka force spring ko change karta hai. Ek spherical ball ko jab hum apne hatho se dono side se press kare toh use ball ke shape me change hoga yeh aap figure me dekh sakte hai. In sare example se hum yeh keh sakte hai ki a force can change the shape and size of body

Forces do prakar ki hoti hai
- a) Balanced Force
b) Unbalanced force
Balanced force :
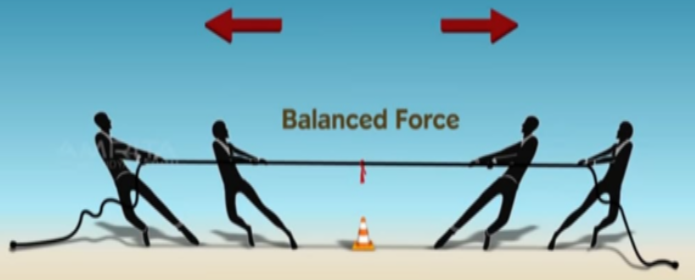
Jitne bhi force body me lag rahe ho aur un forces ka resultant zero ho tab use balanced force kehte hai. Koi body ager balanced force me hai tab woh body apni position change nahi karega (rest or of uniform motion), wo aisi appear hoga jaise us pr koi force nahi hai.
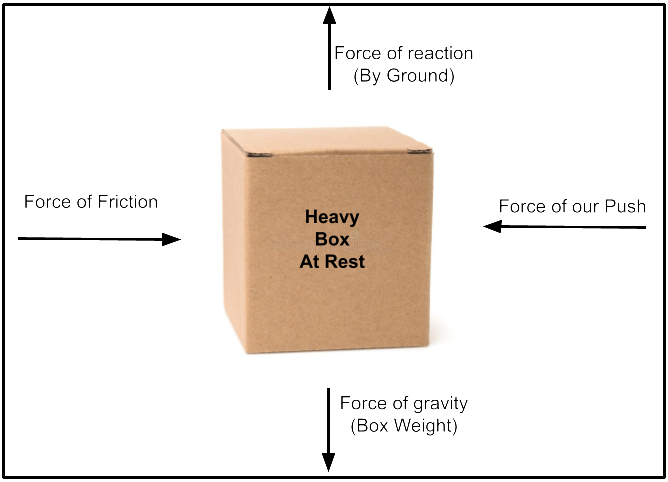
Let’s do an experiment, hum ek heavy box jo ground pr rakha ho use is experiment ke liye use karenge. Ab us box ko hum apne hato se push karenge, tab woh box apni position se move nahi karega woh rest position me hi rahega, tab hum yeh dekhenge ki is box pr 4 force act honge aur wo yeh hai :
- Force jab humne box push karne me lagaya.
- Force of friction jo oppose karta hai push force ko aur box ko move nahi karne deta.
- Force of gravity jo box ko downwards direction me pull karega.
- Force of reaction jo ground ke karan box me upwards direction me lagega, yeh force gravity ko balance karta hai.
So, box pr 4 force lag raha hai pr box move nahi ho raha aur wo rest position me hai, tab is se yeh conclude hota hai ki sare force ka resultant zero hai. Thus, ye box aise behave karta hai ki is pr koi force nahi lag raha ho.
Aisi hi box jo stationary position me ho wo sare balanced force ke example hai. Note : In this experiment :
- Force of push = Force of friction.
- Force of gravity = Force of Reaction.
Similarly, ager stationary body pr number of balanced force act ho rahe hai tab bhi wo body move nahi karega woh rest pr hi rahega, aise hi ager balanced force body pr uniform motion me lagega tab bhi body uniform motion ke state me rahega.
Though balance force motion produce nahi karta kisi bhi stationary body me aur wo kisi moving body ko bhi stop nahi kr sakta, pr wo body ke shape ko change kr sakta hai. For example agar hum kisi rubber ball or balloon ko squeez kre tab inke shape me change hoga. Is case me hum 2 force laga rahe hai equal and opposite direction me (balanced force) apne hatho se. Through the ball and balloon apni position change nahi karte.

Unbalanced force :
Jitne bhi forces body me lag rahe ho aur unka resultant zero na ho tab us forces ko hum unbalanced force kahte hai. Unbalanced force body ko movement se rest position me aur rest position se motion me lata hai.- Unbalanced force body ke speed or direction ko change karta hai.
- Force of our push
- Force of friction
- Force of gravity
- Force of reaction of ground.
Is case me car me jo gravitational force lag raha hai uska opposing force ground se aa raha hai wo reaction force hai jo ki gravitational force ke barabar hai, iska matlab Gforce=Rforce, isliye yaha pe ye balanced force hai. Ab toy car me wheel ki wajah se force of friction kam hai jab humne car ko push kiya to usme jo push force hai wo force of friction se jayda hai iski wajah se car force ki direction ki ore agge badgi. Is liye dono force unbalanced hai yaha pe resultant force zero hoga.
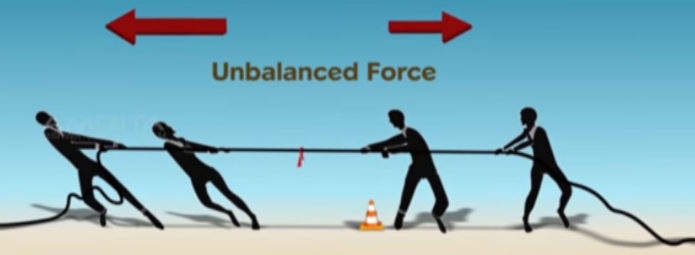
Uper image me aap dekh sakte hai ki yaha pe force unbalanced hai. Left side me pulling force jyada hai isliye rope left side walo ki taraf hai aur wo ye game win kr rahe hai. Ager right side wale suddenly rope ko release kr dete hai to left side walo ke force ki wajah se woh piche ki taraf fall honge. Is se ye proof hota hai ki jab body me unbalanced force hota hai to body move karta hai.
Isi tarah unbalanced force body ko movement se bhi rest position me lata hai. Eg: Jab ek ball ground me roll kr raha ho kuchh der me wo ball stop ho jayga kyunki ball me force of friction laga raha hota hai.

POINT 1
Force :
It is a push or pulls on an object that produces an acceleration in the body on which it acts. S.I. unit of force is Newton.
Balanced Force :
Forces are said to be balanced forces if they nullify one another and their resultant force is zero.
Frictional Force :
The force that always opposes the motion of objects is called a force of friction.
Unbalanced Force :
When two opposite forces acting on a body, move a body in the direction of the greater force or forces which bring motion in a body are called as unbalanced forces.
NEWTON’S FIRST LAW OF MOTION
Newton’s Law Of Motion :

Sir Issac Newton ne teen law likhe hai body ke motion ko describe karne ke liye, aur ise Newton’s law of motion kahte hai. Is law se hume body me jo force lagte use padhenge.
First Law of Motion :-
First law kehta hai ki Jab koi body rest me ho to wo rest me hi rahega or jab body move kr raha ho straight line me wo move hi karta rahega, jab tak us body me koi external force apply nahi hota tab tak wo same position maintain karega.External force ka matlab jab body body ka force nahi hota us body pr bahar se lagne wale forces ko external force kahte hai. For example ek book table pr rest position me hai, ye book apna position change nahi kar sakti, jab hum is book ko lift karenge to humare hatho ke force ki wajah se book apni position change karega, humare hatho ka force external force hai. Aur ye example first law ko follow karta hai.
Newton's First Law of motion in our daily life :
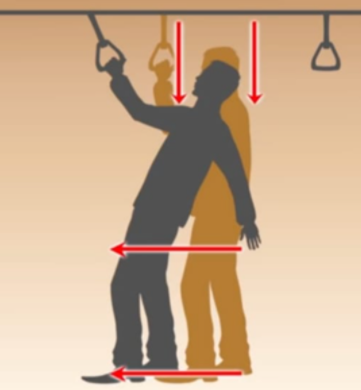
- (a) A person standing in a bus falls backward when moves suddenly.
Aisa isliye hota h kyunki jab bus rest me ho to person jo bus ke ander hai wo bhi rest me rahege, pr jab bus move karne lagega to person ke legs me bhi movement hogi bus ke karan jabki uski body ki tendency rest me hogi.isliye wo backward fall karega.
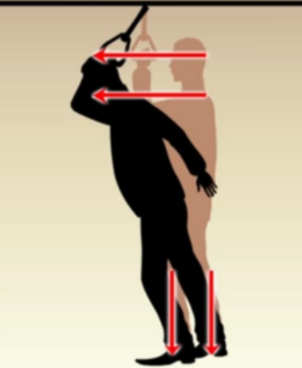
(b) Similarly, a person is standing in a bus and the bus suddenly stops then they will fall in forward direction.
Aisa isliye hota hai kyuki jab bus motion me hota hai to person bhi motion me hota hai kyuki wo bus ke surface pr khada hai, pr jab bus suddenly ruk jata hai to person ke leg ki movement bhi ruk jati hai pr uske body ki tendency movement me hoti hai is liye wo person bus ke suddenly rukne pr aage ki taraf girega ager wo alert nahi hai to.


Inertia :
Ye body ki wo property hai jisme body resist karta hai state of rest ke change ko or uniform motion ko. Jitna jyada hoga body me inertia utna hi jyada force lagega body ko move karne me. In Fact a mass is a measure of inertia of a body. Matlab ager body ka mass jyada hai to uska inertia bhi jyada hoga. Example ek stone me jayda inertia hai football se, cricket ball ka inertia jyada hai rubber ball se. Consider kre body A ka weight 1 kg hai aur body B ka weight 20 kg, to yaha pr inertia body B ka jyada ho hoga body A se. Is se hum ye conclude kr sakte hai ki to overcome inertia and make body move we must apply external force.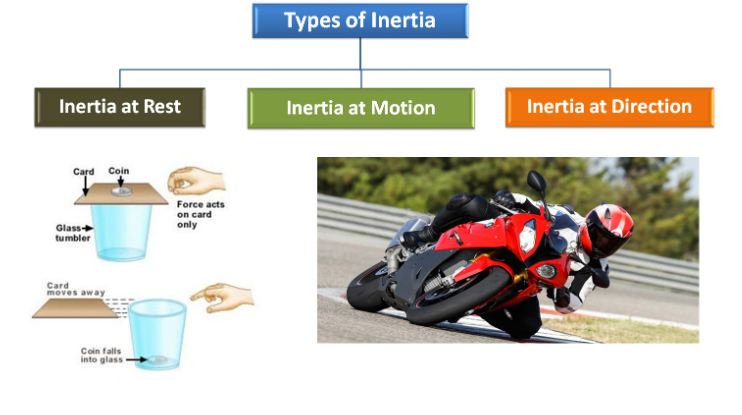
Jaise ki uper figure me hum dekh sakte ki ek glass ke upar ek cardboard rakha hai aur uske center me ek coin jo ki rest postion me hai. Jab hum card ko flick kare to card motion me ayega pr coin rest pr hi rahega is liye jab board glass se hat jayega to coin glass me gir jayega.
Newton’s First law of motion ke second part me humne dekha ki body jab movement kr raha ho toh move karta hi rahega jab tak us pr koi external force nahi lagta hai. Aap ko ye glt lag raha hoga, chaliye isi ek example se samjhte hai, ek cycle ko jab paddle karte hai to wo chalne lagti hai, aur ager hum use constant force se paddle kr rahe to wo constant speed me hogi, pr jab hum cycle ko paddle karna band kr de to wo kuch der baad ruk jaygi, pr first law kehta hai ki jab body motion me ho tab wo continue motion me rahegi jab tak uspr koi external force na lage. Yaha cycle is liye ruk jati hai kyunki cycle air resist karta hai matlab cycle pr air ka force lagta hai aur friction force bhi jiski wajah se wo ruk jata hai. Isliye ye first law of motion ko satisfy karta hai.


Momentum :
Second law ko padhne se pehle hume hume momentum ke bare me padhna jaruri hai. Jaise ki hum jante hai cricket ball or tennis ball ke mass me difference hai. Ager hum dono balls ko throw kre same speed me me toh cricket ball ko stop karne ke liye hume jyada force lagega tennis ball ko stop karne me se. Isse hum ye conclude karte hai ki force to stop a moving body is directly proportional to its mass. Ager hum do cricket ball jiska mass same ho use alag alag speed or velocity se throw kre, to hum ye found karenge ki jyada velocity wale ball ko rokne ke liye jyada force lagega km velocity wale ball se. Isse hum ye conclude kr sakte hai ki force to stop a moving body is directly proportional to its velocity. Isliye body ki quantity mass or velocity pe depend karti hai aur is dependence ko hum momentum kahte hai. The momentum of a body is defined as the product of mass and velocity.- Momentum = mass × velocity.
or, p=m×v
where, p = momentum, m = mass of body and v = speed or velocity of a body.
Ager body rest mai hai to momentum zero hoga. Isliye total momentum of gun and bullet is zero before firing.
- Momentum ek vector quantity hai aur iska direction velocity ke taraf hoga.
- SI unit of momentum is kgmsec.

EXAMPLE 1
What is the momentum of a man of mass 75 kg when he walks with a uniform velocity of 2m/s ?
Given data :
- m = 75 kg, v = 2 msec,
we know that : p=mv,
so, momentum (p) = 75 kg× 2 msec
p = 150 kgmsec.
Therefore momentum of a man is 150 kgmsec.
EXAMPLE 2
What is the acceleration produced by a force of 12 newtons exerted on an object of mass 3 kg
Here, Force, F= 12 N
Mass, m=3 kg
And, Acceleration, a= ? (To be calculated)
We know that: F=m×a
So, 12=3×a
3a=12
a=123ms2
or Acceleration, a = 4 m/s2
EXAMPLE 3
A force of 5 newtons gives a mass m1 an acceleration of 8m/s2, and a mass m2 an acceleration of 24m/s2. What acceleration would it give if both the masses are tied together?
(i) In the first case:
Force, F=5 N
Mass,m=m1 (To be calculated)
And, Acceleration, a = 8 m/s2
Now, F=m×a
So, 5=m1×8
And, m1=58kg
m1=0.625kg
Thus, the mass m1 is 0.625 kg.
(ii) In the second case:
Force, F = 5 N
Mass, m=m2 (To be calculated)
And, Acceleration a=24 m/s2
Now, F=m×a
So, 5=m2×24
And, m2=524kg
m2=0.208 kg
Thus, the mass m2 is 0.208 kg.
(iii) In the third case:
Force=5N
Total mass, m = m1+m2.
=0.625+0.208
=0.833 kg
And, Acceleration, a = ? (To be calculated)
Now putting these values in the relation :
F=m×a
We get : 5=0.833×a
a=50.833
a=6m/s2
Thus, if both the masses are tied together, then the acceleration would be 6 m/s2
EXAMPLE 4
A bullet of mass 10 g is fired from a gun of mass 6 kg with a velocity of 300 m/s. Calculate the recoil velocity of the gun.

Here, Mass of bullet= 10 g
=10100 kg
=0.01 kg
Velocity of bullet= 300 m/s
Mass of gun=6kg
And, Recoil velocity of gun=? (To be calculated)
Now, putting these values in the relation :
Mass of bullet ×Velocity of bullet×=mass of gun ×Recoil velocity of gun
We get : 0.01×300=6× Recoil velocity of gun
So, Recoil velocity of gun =0.01×3006
=0.5 m/s
Note: The above problem can also be solved by calculating the momentum of bullet and the gun separately as follows :
Momentum of bullet= Mass of bullet×Velocity of bullet
=0.01×300
= 3 kg. m/s
Now, suppose the recoil velocity of gun is v m/s.
So, Momentum of gun= Mass×Recoil velocity of gun
=6×v kg m/s
According to the law of conservation of momentum :
So, 3=6×v
And, v=36m/s
Recoil velocity of gun,v= 0.5 m/s.
EXAMPLE 5
Which of the following has more inertia: (a) a rubber ball and a stone of the same size? (b) a bicycle and a train? (c) a fiverupees coin and a one-rupee coin?
Inertia is the measure of the mass of the body. The greater is the mass of the body, the greater is its inertia and vice-versa.
(a) Mass of a stone is more than the mass of a rubber ball for the same size. Hence, inertia of the stone is greater than that of a rubber ball.
(b) Mass of a train is more than the mass of a bicycle. Hence, inertia of the train is greater than that of the bicycle.
(c) Mass of a five rupee coin is more than that of a one-rupee coin. Hence, inertia of the five rupee coin is greater than that of the one-rupee coin.
NEWTON’S SECOND LAW OF MOTION
Jab do body le, ek heavy weight ka aur dusra lightweight ka aur dono body pr ek hi force se push kare to jo lighter body hai wo jayda force gain karega heavyweight object se. Pr momentum jo dono body gain karega wo same hoga. Ye jo link hai force aur momentum ke beech use second law ne explain kiya hai.
Second law ke anusar body ke momentum ke rate me jo change hoga wo directly proportional hota hai force se jo us body me apply kiya hua hai, aur momentum force ke direction me hoga. Rate of change of momentum can be obtained by time taken for change. So, Newton's second law is expressed as :
- Force∝Change in MomentumTime Taken
Consider kare ek body ka mass m hai aur uska initial velocity u hai, to initial momentum of a body is mu. Suppose kare ek force F is body pr laga aur uski wajah se body ka velocity me badlav aya to final velocity hui body ki v, to final momentum hoga body ka mv. The change in momentum of body is mv−mu and time taken for change is t, then according to Newton’s second law :
- Force ∝ mv−mut,
or F ∝ m(v−u)t
but v−ut is acceleration a, so from this relation we can write as :
- F∝ma.
Is relation se ye pata chalta hai ki force ki wajah se mass or acceleration ka product banta hai.
- F=k×m×a
- F=m×a
Newton’s second law of motion hume force or acceleration ke beech ka relation batata hai. 2nd law hume force ko mass or acceleration ke terms me batata hai.
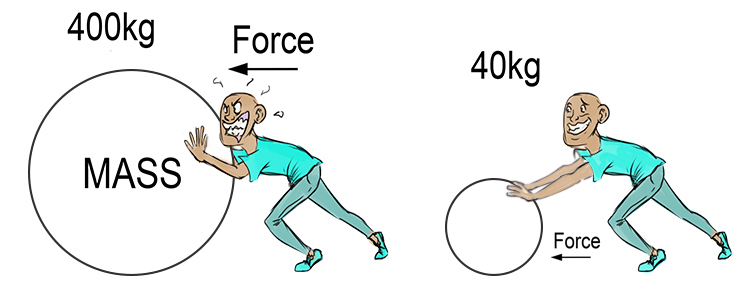
- a=Fm
Is relation se hume ye pata chalta hai ki force directly proportional hai acceleration ke. Aur m inversely proportion hai force ke. Isse ye pata chalta hai ki ager mass double ho jaye to acceleration half ho jata hai, aur agar acceleration double ho to mass half ho jata hai. So, lighter body ko move karna easy hai heavy bodies se.
Force ka SI unit Newton hai or isko N se denote karte hai. Newton ek aisa force hai jo 1 kg body me act ho raha hai aur uska acceleration hai 1 ms2 to :
- 1 Newton = 1kg×1ms2
OMR (One Minute Revision)
- *Ager acceleration -ve me hai to iska matlab acceleration ka direction opposite hai body ke movement se.
* Ager force -ve sign ke sath hai to iska matlb force opposite se act ho raha hai motion ke.
Applications of Second Law
Humare daily life ko ager hum observe kre to hum daily basis me kahi na kahi second law ko follow karte hai. Kuchh examples second law ke :1. Catching a Cricket Ball : Jab cricket player fast moving ball ko catch karta hai to ball ko catch karte hi apne hato ko piche ki taraf lata hai, aisa player isliye karta hai kyu wo apne hato ko injured hone se bachta hai. Jab ball bahut teji se travel kr raha hota hai to uski momentum bahut jyada hodi hai, player ball ke momentum ko reduce karne ke liye hatho ko piche ke or lata hai iski wajah se momentum ko reduce karne ke time mil jata hai jiski wajah se player ko koi injury nahi hoti.
Ager player fast ball ko catch karta hai bina koi movement ke, to ball ke momentum ki wajah se wo injured ho sakta hai kyuki jo large amount of momentum suddenly zero ho jata hai. Iski wajah se player ke hatho me force bahut jyada lagega. Isi aap niche diye gaye image me observe kr sakte hai.
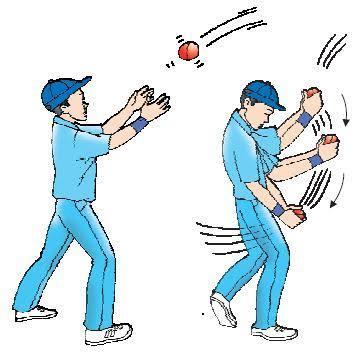
2. The case of High Jumper : Sabhi sports event me high jumper ko cushion or sand ko ground me provide kiya jata hai. Ye injury ko prevent karne ke liye kiya jata hai. Jab high jumper, jump ke bad wo sand aur cushion me land karta hai to use stop hone me thoda time lagta hai jiski wajah se jumper ke body ki momentum slowly reduce ho kr zero hoti hai aur jumper injured nahi hota. Ager jumper directly solid ground me land karta hai to uski body ke momentum suddenly zero ho jati hai aur uske body pe jayda force lagta hai aur wo injured ho jata hai.

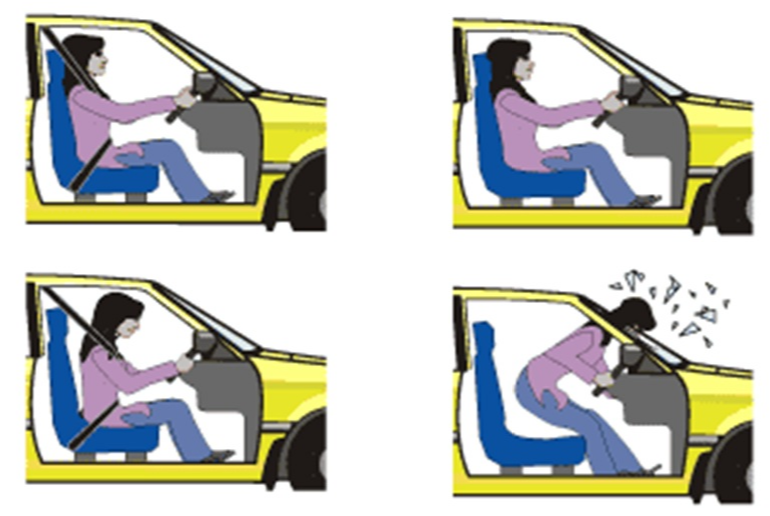
3. The Use of Seat Belts in Car : Apne ne dekha hoga ki cars me seat belt hota hai passengers ke liye. Ye seat belt passengers ko injury se bachane ke liye hota hai. Jab kar ka accident hota hai to car ki momentum suddenly zero ho jati hai jiski wajah se passenger ki momentum bhi zero hone lagti hai pr seat belt ki wajah se passenger ke momentum slowly reduce hota hai jiski wajah se wo less injured hota ya fir injured hi nahi hota.
POINT 2
First Law of Motion :
An object remains in a state of rest or of uniform motion in a straight line unless acted upon by an external unbalanced force.
Inertia :
The natural tendency of an object to resist a change in their state of rest or of uniform motion is called inertia.
The mass of an object is a measure of its inertia.
Its S.I. unit is kg.
A body with greater mass has greater inertia.
The Second Law Of Motion :
The rate of change of momentum of an object is proportional to the applied unbalanced force in the direction of the force.
Momentum :
The momentum of an object is the product of its mass and velocity and has the same direction as that of the velocity. It's S.I. unit is kg m/s.
1 Newton :
A force of one Newton produces an acceleration of 1 m/s2 on an object of mass 1 kg.
- 1 N = 1 kg m/s2 (F = ma).
EXAMPLE 6
What force would be needed to produce an acceleration of 4 ms2 in a ball of mass 6 kg ?
The force needed to be calculated by using the relation :
- Force = mass x acceleration
or F=ma
Here, Force F = ? , mass m = 6 kg, and acceleration = 4 ms2
Putting the values in above equation we get :
- F = 6 x 4 = 20 N
The force needed is of 20 newtons.
EXAMPLE 7
Calculate the force required to impart to a car a velocity of 30 m/s in 10 seconds starting from rest. The mass of the car is 1500 kg.
Given data :
- Mass, m = 1500 kg,
By using 1st equation of motion we get : v = u + a t.
Putting values, 30 = 0 + a x 10
10 a = 30
a=3010ms2
Acceleration, a = 3ms2.
- F = 1500 x 3 N = 4500 N.
EXAMPLE 8
Which would require a greater force - accelerating a 10 g mass at 5 m/ s2 or 20 g mass at 2 m/s2?
(i) In first case: Force, F=m×a
=101000kg×5m/s2
=0.05N
(ii) In second case : Force,F=201000kg×2m/s2
=0.04 N
Thus, a greater force of 0.05 N is required for accelerating a 10 g mass.
EXAMPLE 9
In the following example, try to identify the number of times the velocity of the ball changes: “A football player kicks a football to another player of his team who kicks the football towards the goal. The goalkeeper of the opposite team collects the football and kicks it towards a player of his own team”.
Also identify the agent supplying the force in each case.
The velocity of the ball changes four times.
First, when a football kicks to another player, second when that player kicks the football to the goalkeeper. Third when the goalkeeper stops the football. Fourth when the goalkeeper kicks the football towards a palyer of his own team.
Agent supplying the force.
Firts case-First player.
Second case- Second player
Third case- Goalkeeper
Fourth case- Goalkeeper
EXAMPLE 10
Two objects of masses 100 g and 200 g are moving along the same line and direction with velocities of 2 ms−1 and 1 m s−1, respectively. They collide and after the collision, the first object moves at a velocity of 1.67 m s−1. Determine the velocity of the second object
Mass of one of the objects, m1=100g=0.1kg
Mass of the other object, m2=200g=0.2kg
Velocity of m1 before collision, v1=2m/s
Velocity of m2 before collision, v2=1m/s
Velocity ofm1 after collision, v3=1.67m/s
Velocity of m2 after collision =v4
According to the law of conservation of momentum:
Total momentum before collision = Total momentum after collision
Therefore m1v1+m2v2=m1v3+m2v4
2(0.1)+1(0.2)=1.67(0.1)+v4(0.2)
0.4=0.67+0.2v4
v4=1.165 m/s
Hence, the velocity of the second object becomes 1.165 m/s after the collision.
NEWTON’S THIRD LAW OF MOTION
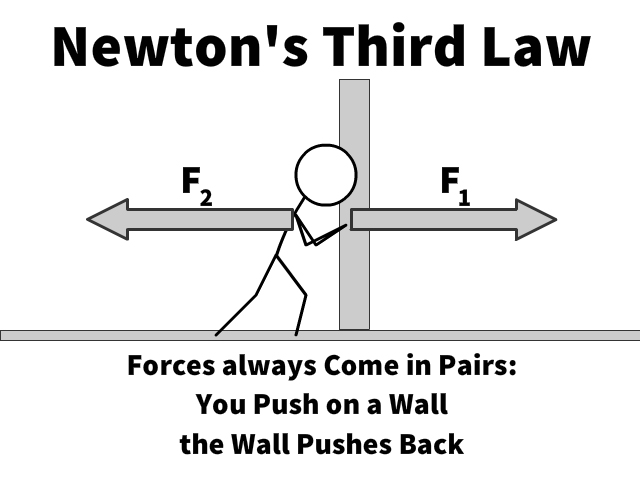
Newton’s third law states that Every action has an equal and opposite reaction. Iska mtlb jab kabhi bhi kisi body me force lagta hai wo itna hi force opposite direction me release karta hai. Chaliye ise ek example se samjhte hai :

Jaise ki app image me dekh sakte hai ki jab hum ball ko ground ki taraf kuch force se throw karte hai to ball ground se bounce krke wapas aata hai utne hi force se jitna humne throw karne me lagaya tha.

Jab hum walk karte hai to hum apne legs se ground pe force karte hai jiski wajah se hum aage badte hai, jab hum ground me force lagate hai to ground bhi hume utne hi force se push karti hai.
In examples se hum keh sakte hai ki jitna force kisi pr lagta hai wo utna hi force reaction bhi karta hai.

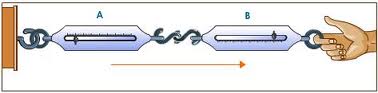
Let’s do an experiment : Aap do same spring le, aur dono spring ke knot ko join kr de, ek spring ke ek end ko wall se fix kr de aur dusre spring ke end ko aap apne hatho se pull kare aap payenge ki aapne jitna force spring ne lagya utna hi reaction force dusre spring ne dia. Ye experiment aap niche fig me dekh sakte hai.
Action and reaction of two different bodies
Suppose ek heavy box ground pr rakha hai. To box ka weight force exert karta hai ground ki taraf. Jo downward force hai ground ki aur ground, to ground bhi react karega aur utna hi force wo upwards direction me exert karega. Yaha pe box ka weight force hai wo action force hai aur jo ground se force aa raha hai wo reaction force hai. Ise se ye pata chalta hai ki action and reaction dono alag alag force hai.

Some examples for 3rd law:
1. When a swimmer swims :

Aap image me dekh sakte hai ki jab swimmer swim karta hai to apne hatho se water ko push karta hai to water utna hi force exert karke swimmer ko push karta hai.
2. Why the Gun Recoils :

Jab bullet fire hota hai gun se to jo force lagta hai bullet pr utna hi reaction force lagta hai gun pr lekin gun ka weight jyada hota hai bullet se isliye gun slightly move hota hai backward side aur gun hath ya shouler me gunner ko gun ke recoil ki tarah mahsus hota hai.
3. The flying of Jet aeroplanes and Rockets :

Jet planes or rockets action or reaction ki principal ko follow karta hai. Jet planes or rockets me hot gas jo fuel ko rapidly burn karne se milta hai wo nozzle se downward direction me exert hota to hot gas rocket ko upward direction me push karta hai.
In sab examples me ek point common hai jo ki hai : Every action there is an equal and opposite reaction. Ye Newton’s third law hai.
CONSERVATION OF MOMENTUM
Second law me humne dekha ki sabhi moving bodies momentum possess karti hai. i.e. Momentum = mass × velocity.
Jo term hai conservation of energy hum isi ek example se samjhege.
Consider kre ki ek heavy truck speed se chal rahe hai aur wo suddenly samne car hai us se takra jati hai to aap ye dekhege ki car piche ki taraf move karega mtlb truck jis direction me move ho raha tha usi direction me, kyu ki car ka mass truck se less hai isliye truck ka momentum car se jyada hota hai. Jab truck car se takrati hai to truck ka momentum km hone lagta hai aur car ka momentum badhne lagta hai. Isse ye proof hota hai ki jitna momentum car ne gain kiya hai collision ke baad utna hi momentum truck ne loss kiya hai. Yaha pe truck ka momentum car ke momentum me badal jata hai. Yahi conservation of momentum hai.
According to law of conservation of momentum when two or more bodies acts upon one another, their total momentum remains constant (or conserved) provide no external force is acting.
Law of momentum kahta hai ki jab ek body momentum gain karta hai to dusre body equal amount me momentum lose karta hai. Moment is neither created nor destroyed Law of conservation of momentum ko Principle of conservation of momentum bhi kaha jata hai.
Example fo Law of conservation of Momentum :
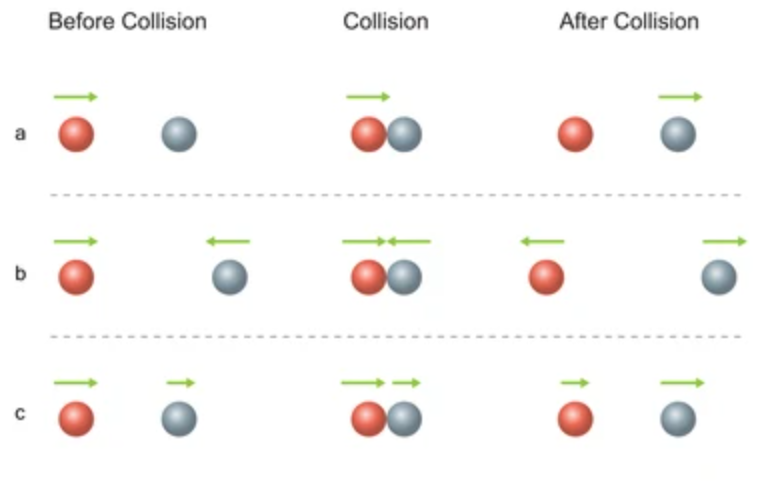
Ye figure law of conservation ka example hai, ye figure me teen case dikhaya gaya hai wo hai :
Case 1 : Jab red ball move kr raha to us pr momentum hai wo aa kr blue ball se collide hota hai jiska weight red ball se thoda jyada hai is liye red ball suddenly stop ho jata hai mtlb red ball ka momentum zero ho jata hai aur blue ball momentum gain karta hai. Blue ball utna hi momentum gain karta hai jitna red ball lose karta hai, aur wo momentum ke direction me move karta hai.
Case 2 : Aap dekh sakte hai ki red ball or blue ball dono ek momentum se opposite direction me move kr rahe hai. Yaha pe dono balls ka mass same hai isliye jab dono ball collide hue to dono ne apna momentum lose kiya aur dusre ball ka momentum gain kiya mtlb red ball ne blue ball ka or blue ball ne red ball ka or wo us momentum ke direction me move karenge. Dono ball same amount ka momentum gain kiya jitna opposite ball ne lose kiya.
Case 3. Jab red ball or blue ball ek hi direction me move kr rahe ho aur red ball ka momentum jayda ho to wo speed se aa kar blue ball ko back side se collide karega jiski wajah se red ball apni kuch momentum lose karta hai aur uski speed decrease hoti or momentum bhi usi tarah blue ball red ball ka momntum gain karega aur uski speed mai increase hogi.
Mathematical Representation For Law of Momentum
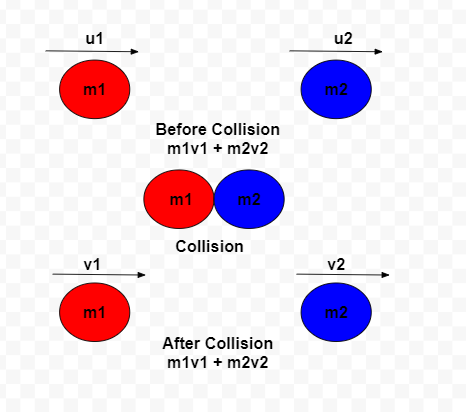
As shown in figure, Yaha pe do balls hai red and blue, jiska mass m1 or m2 hai, Aur unki velocity before collision hai u1 and u2 respectively. So the momentum of the balls is:
Red : (m1)(u1)
After collision velocity of balls are v1 for red and v2 for blue, so the momentum is (m1)(v1) and (m2)(v2). Total momentum after collision is (m1)(v1) + (m2)(v2)
Blue : (m2)(u2)
Suppose during the collision Force exerted by red ball is F1 and in turn blue ball exerts a force F2 to the red ball. AB hum Yaha Force ki value find karenge :
- a2=v2−u2t
- F1=m2×v2−u2t
- a1=v−1−u1t
- F1=m1v1−u1t
- F1 = -F2
m2v2−u2t=−m1v1−u1t
cancelling t on both sides we get,
m2v2−m2u2=m1u1−m1v1
m2v2+m1v1=m1u1+m2u2
Total momentum before collision = Total momentum after collision
EXAMPLE 11
The car A of mass 1500 kg, travelling at 25 m/s collides with another car B of mass 1000 kg travelling at 15 m/s in the same direction. After collision the velocity of car A becomes 20 m/s. Calculate the velocity of car B after the collision.

In order to solve this problem, we will calculate the total momentum of both the cars, before and after the collision.
(a) Momentum of car A(before collision)=Mass ofcar A×Velocity ofcar A
=1500×25
=37500 kg.m/s
Momentum of car B(before collision)=Mass ofcar B×Velocity ofcar B
=1000×15
=15000 kg.ms
Total momentum of car A and car B=37500+15000
(before collision)=52500 kg.m/s
(b) After collision,the velocity of car A of mass 1500 kg becomes 20 m/s.
So, Momentum of car A=1500×20
(after collision)=30000 kg.m/s
After collision, suppose the velocity of car B of mass 1000 kg becomes v m/s
So, Momentum of car B=1000×v
(after collision)=1000 v kg.m/s
Total momentum of car A and B = 30000+1000 v.......(2)
(after collision)
Now, according to the law of conservation of momentum :
Total momentum=Total momentum
before collision after collision
That is, 52500=30000+1000 v
1000 v=52500-30000
1000 v=22500
v=225001000
v=22.5 m/s
Thus, the velocity of car B after the collision will be 22.5 m/s.
EXAMPLE 12
A bullet of mass 10 g moving with a velocity of 400 m/s gets embedded in a freely suspended wooden block of mass 900 g. What is the velocity acquired by the block ?

Here, Mass of the bullet,m1=10g
=101000kg
=0.01 kg
And, Velocity of the bullet, v1=400 m/s
So, Momentum of bullet=m1×v1
=0.01×400kg.m/s…….(1)
Now, this bullet of mass 10 g gets embedded into a wooden block of mass 900 g . So ,the mass of wooden blockk alongwith the embedded bullet will become 900+10=910 g. Thus,
Mass of wooden block+Bullet, m2=900+10
=910 g
=9101000 kg
=0.91 kg
And, Velocity of wooden block+bullet,v2=? (To be calculated)
So, Momentum of wooden block+bullet=m2×v2
=0.91×v2kg.m/s...(2)
Now, according to the law of conservation of momentum, the two momenta as given by equations (1) and (2) should be equal.
So, m1×v1=m2×v2
or 0.01×400=0.91×v2
And, v2=0.01×4000.91
=4.4 m/s
Thus, the velocity acquired by the wooden block (having the bullet embedded in it) is 4.4 metres per second.
EXAMPLE 13
A batsman hits a cricket ball which then rolls on a level ground. After covering a short distance, the ball comes to rest. The ball slows to a stop because
(a) the batsman did not hit the ball hard enough.
(b) velocity is proportional to the force exerted on the ball.
(c) there is a force on the ball opposing the motion.
(d) there is no unbalanced force on the ball, so the ball would want to come to rest.
The ball slows down and comes to rest due to opposing foreces or air resistance and frictional force on the ball opposing its motion. Therefore the choice (c) there is a force on the ball opposing the motion is correct.
EXAMPLE 14
A stone of 1 kg is thrown with a velocity of 20 m s−1 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice?
Initial velocity of the stone, u = 20 m/s
Final velocity of the stone, v = 0
Distance covered by the stone, s = 50 m
Since, v2−u2=2as
Or, 0−202=2a×50,
Or , a=−4ms−2
Force of friction, F=ma= -4N
EXAMPLE 15
A truck starts from rest and rolls down a hill with constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force acting on it if its mass is 7 metric tonnes.
First of all we find its accelrating by using the relation:
Distance travelled,s=ut+12at2
Here,Distance travelled, s =400 m
Initial speed, u=0 (It starts from rest)
Time, t = 20 s
and Acceleration, a=? (To be calculated)
Putting these values in the above formula, we get :
400=0×10+12×a×(20)2
400=200a
a=400200
Acceleration,a=2m/s2
We will now calculate the force by using the relation: .....(1)
F=m×a
Here Mass, m =7 metric tonnes
=7×1000kg ....(2)
And, Acceleration, a = 2 m/s2 (Calculated above)
So, Force, F = 7000×2
F=14000 N
Thus, the force acting on the truck is 14000 newtons.
EXAMPLE 16
The speed-time graph of a car is given alongside. The car weighs 1000 kg
(i) What is the distance travelled by the car in the first two seconds?
(ii) What is the braking force applied at the end of 5 seconds to bring the car to a stop within one second?

(i) We will first calculate the distance travelled in the first two seconds. From the given graph we find that :
Distance travelled in first two seconds = Area under line AB and the time axis
=Area of triangle AB2
=12×base×Height
=12×2×15
=15 m
Thus, the distance travelled by the car in the first two seconds is 15 metres.
(ii) The braking force is to be calculated by using the formula
Force=mass×acceleration
or F=m×a
Here, the mass of the car is given as 1000 kg but the acceleration in the last one second (from point C to point D) is to be obtained from the graph shown above. Now, we know that the acceleration is given by the slope of speed-time graph. So,
Acceleration in last one second = Slope of line CD
=PerpendicularBase
=151
=15m/s2
If we look at the above given graph, we will find that the speed of the car is decreasing from point C to point D. That is, the acceleration from C to D is negative and hence it should be written with a minus sign. Thus,
Acceleration, a =-15 m/s2
Now,putting m= 1000 kg and a =15 m/s2 in formula (1), we get:
Force,F=1000 × (-15)
=-15000N
Thus, the force applied by the brakes to stop the car is 15000 newtons. The negative sign of force here shows that the force is being applied in a direction opposite to the motion of the car. That is, it is a retarding force.
POINT 3
Third Law of Motion :
To every action, there is an equal and opposite reaction and they act on two different bodies.
Conservation of Momentum :
If the external force on a system is zero, the momentum of the system remains constant i.e., in an isolated system, the total momentum remains conserved.

Suppose A and B are two balls, they have mass mA and and initial velocities uA and uB as shown in above figure before collision. The two bodies collide and force is exerted by each body. There is change in their velocities due to collision.
(mAuA+mAuB) is the total momentum of the two balls A and B before collision and (mAvA+mBvB) is their total momentum after the collision.
The sum of momenta of the two objects before collision is equal to the sum of momentum after the collision, provided there is no external unbalanced force acting on them.
This is known as the law of conservation of momentum.
SUMMARY
- First law of motion: An object continues to be in a state of rest or of uniform motion along a straight line unless acted upon by an unbalanced force.
- The natural tendency of objects to resist a change in their state of rest or of uniform motion is called inertia.
- The mass of an object is a measure of its inertia. Its SI unit is kilogram (kg).
- Force of friction always opposes motion of objects.
- Second law of motion: The rate of change of momentum of an object is proportional to the applied unbalanced force in the direction of the force.
- The SI unit of force is kgms−2. This is also known as newton and represented by the symbol N. A force of one newton produces an acceleration of 1 m s−2 on an object of mass 1 kg.
- The momentum of an object is the product of its mass and velocity and has the same direction as that of the velocity. Its SI unit is kg m s−1.
- Third law of motion: To every action, there is an equal and opposite reaction and they act on two different bodies.
- In an isolated system (where there is no external force), the total momentum remains conserved.