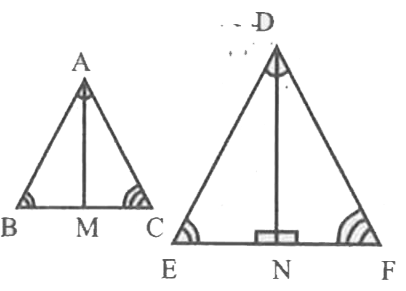
The area of two equilateral triangles are in the ratio 25 : 36 . Their altitudes will be in the ratio:
1 36 : 25
2 25 : 36
3 5 : 6
4 √5 : √6
Answer : 3. "5 : 6 " Explanation :the ratio will be squre root of triangle so that answer will
Related Solutions
The areas of two equilateral triangles are in the ratio 25:36. Their altitudes will be in the ratio (a) 25:36 (b) 36:25 (c) 5:6 (d)
View SolutionThe areas of two equilateral triangles are in the ratio 25:36. What will be the ratio of their vertices?
View Solutionदो समबाहु त्रिभुजों के क्षेत्रफलों का अनुपात हैं उनके शीर्षलम्बों का अनुपात है।
View SolutionThe areas of two equilateral triangles are in the ratio 25:36. Their altitudes will be in the ratio (a) 25:36 (b) 36:25 (c) 5:6 (d)
View SolutionIf the ratio of areas of two equilateral triangles is 25 : 36, then find the ratio of heights of the triangles.
View SolutionTwo isosceles triangles have equal vertical angles and their areas are in the ratio 36 : 25. Find the ratio of their corresponding altitudes.
View Solutionদুটি সমবাহু ত্রিভুজের ক্ষেত্রফলের অনুপাত 16 : 25 হলে, তাদের উচ্চতার অনুপাত কত ?
View Solutionদুটি সমবাহু ত্রিভুজের ক্ষেত্রফলের অনুপাত 16 : 25 হলে, তাদের উচ্চতার অনুপাত হল—
View Solutionଦୁଇ ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ 25:36 ହେଲେ ସେହି ତ୍ରିଭୁଜ ଦ୍ଵୟର ଅନୁରୂପ ବାହୁଯୋଡାର ଅନୁପାତ କେତେ ?
View SolutionThe areas of the similar triangles are the ratio of . What is the ratio of their respectively heights :
View SolutionThe areas of the similar triangles are the ratio of . What is the ratio of their respectively heights :
View Solutionଦୁଇଟି ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ ହେଲେ ସେହି ତ୍ରିଭୁଜଦ୍ବୟର ଅନୁରୂପ ବାହୁ ଯୋଡ଼ାର ଅନୁପାତ କେତେ ?
View SolutionThe ratio between the areas of two similar triangles is 16 : 25. Find the ratio between their :
corresponding altitudes.
View SolutionThe ratio of the circumferences of two equilateral triangles is 25:16, the ratio of the odd sides = _________
View SolutionThe ratio of base of two triangles is x:y and that of their areas is a: b. Then the ratio of their corresponding altitudes will be:
View SolutionIf the altitude of two similar triangles are in the ratio , what is the ratio of their areas?
View SolutionIf the altitude of two similar triangles are in the ratio , what is the ratio of their areas?
View SolutionIf the altitude of two similar triangle are in the ratio 2:3 what is the ratio of their areas?
View SolutionProve that " the ratio of areas of two similar triangles is equal to the square of the ratio of their altitudes.
View SolutionThe areas of two circles are in the ratio 25:36. Find the ratio of their circumferences.
View Solution