AX=0 to x=A/2 ans is T/12 B x=A to x=A/2 is T/6 How to calculate the time period from that equation?

A simple pendulum performs simple harmonic motion about x=0 with an amplitude a ans time period T. The speed of the pendulum at x = (a)/(2) will be

View Solution

A simple pendulum performs simple harmonic motion about x=0 with an amplitude a ans time period T. The speed of the pendulum at x = (a)/(2) will be

View Solution

A simple pendulum performs simple harmonic motion about $x = 0$ with an amplitude a ans time period T. The speed of the pendulum at $x = \frac{a}{2}$ will be

View Solution

यदि समीकरण $x^{2} + a x + 12 = 0$ का एक मूल 4 है तथा समीकरण $x^{2} + a x + b = 0$ के मूल समान हैं, तो b का मान होगा

View Solution

एक सरल आवर्त दोलक का आयाम a तथा आवर्तकाल T इसे $x = 0$ से $x = a / 2$ जाने में लगा समय है

View Solution

if f(x) is an odd periodic function defined on interval [-T/2,T/2], where T is the time period of f(x). Then time period of phi(x)=int_(a)^(x)f(x)dx is

View Solution

Which of the following equations in parametric form can represent a hyperbolic profile, where t is a parameter: (A)x=(a)/(2)(t+(1)/(t))&y=(b)/(2)(t-(1)/(t))(B)t(x)/(a)-(y)/(b)+t=0&(x)/(a)+t(y)/(b)-1=0(C)x=e^(t)+e^(-t)&y=e^(t)-e^(-t)(D)x^(2)-6=2cos t&y^(2)+2=4cos^((t)/(2))

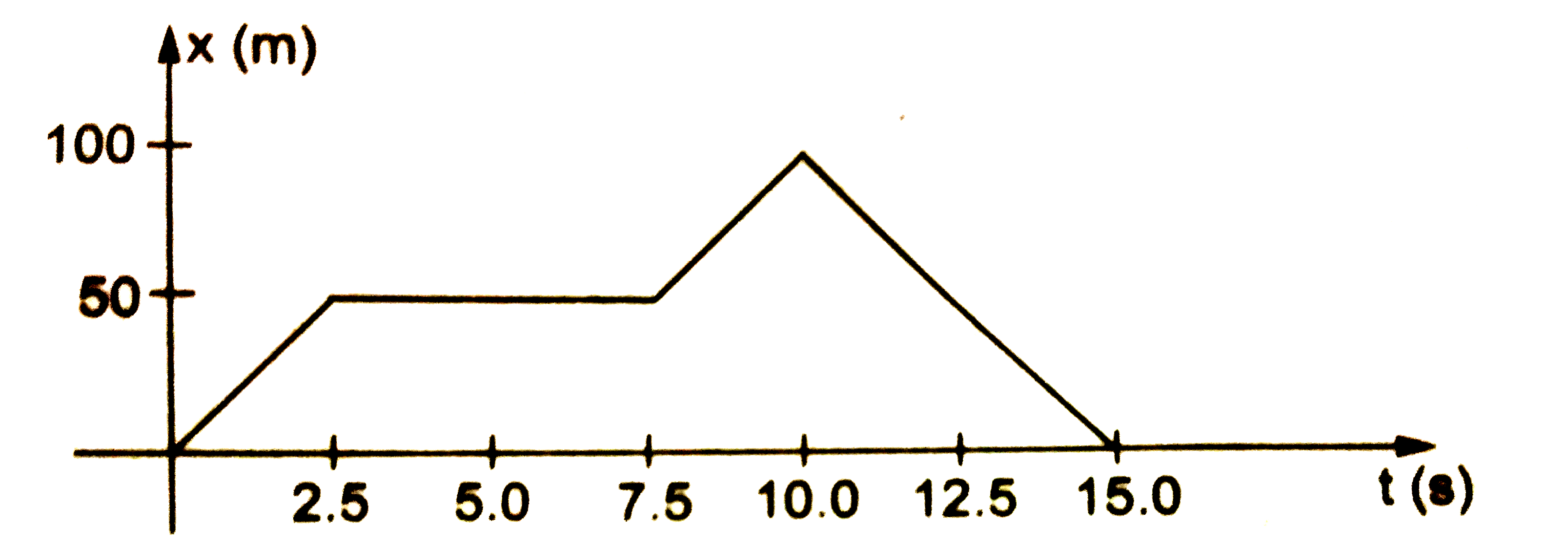
View Solution

चित्र में x - अक्ष पर चलते हुए एक कण का x - निर्देशांक समय के फलां के रूप में दिखाया गया है | ज्ञात करे, (a) t = 0 से t = 10s के अंतराल में औसत वेग (b) 2, 5, 8 तथा 12 s पर कण के वेग |
ocr_image

View Solution

A body oscillates with SHM according to the equation x(t)=5cos(2pit+pi//4) where t is in second and x in metres. Calculate (a) displacement at t=0 (b) time period (c) initial velocity

View Solution

If $x$ satisfies the equation $x^{2} (\int_{0}^{\frac{π}{2}} (2 \sin t + 3 \cos t) d t) - x (\int_{- 3}^{3} \frac{t^{2} \sin 2 t}{t^{2} + 1}) - 2 = 0$ ,then the value of $x$ is

View Solution

If f (x) is periodic function with period T, then the function f (ax+b) where a gt 0, is periodic with period

View Solution

Prove that if $f (x)$ is periodic function with period T, then the function $f (a x + b)$ where $a > 0,$ is periodic with period

View Solution

The displacement of a particle undergoing S.H.M. as a function of time t is given by
$x = A \sin (\frac{4 π t}{3})$
Where x is in cm and t in second
The time taken by the particle to travel from (a) x = 0 to A/2 is $t_{a}$ and time taken by it to travel from (b) x = A/2 to A is $t_{b}$ . Calculate the ratio $t_{b} / t_{a}$ .

View Solution

Let the function x(t) and y(t) satisfy the differential equations (dy)/(dt)+ax=0,(dy)/(dt)+by=0. If x(0)=2,y(0)=1 and (x(1))/(y(1))=(3)/(2), then x(t)=y(t) for t=

View Solution

If a body of mass 36 gm moves with SHM of amplitude A=13cm and period T=12 sec. At a time t=0 the displacement isd x=+13 cm. The shortest time of passage from x=+6.5cm to x=-6.5 is

View Solution

If a body of mass 36 gm moves with S.H.M. of amplitude A = 13 cm and period T = 12 sec. At a time t = 0 the displacement is x = +13 cm. The shortest time of passage from x = +6.5 cm to x = -6.5 is

View Solution

If the roots of the equation $x^{3} + a x^{2} - b x - 6 = 0$ be -1 and 2, calculate the value of a and b.

View Solution

The equation of the tangent to the curve $x = \frac{t - 1}{t + 1}, y = \frac{t + 1}{t - 1}$ at t = 2 is a) $x + 9 y - 6 = 0$ b) $9 x - y - 6 = 0$ c) $9 x + y + 6 = 0$ d) $9 x + y - 6 = 0$

View Solution

If T = time period and A = Amplitude then what is the time required to travel from x = A to x = $\frac{A}{2}$ for any particle maintaing S.H.M.?

View Solution

A simple haramonic motion has an amplitude A and time period T. The time required by ut to travel from x = A to $x = \frac{A}{2}$ is

View Solution

AX=0 to x=A/2 ans is T/12 B x=A to x=A/2 is T/6 How to calculate the time period from that equation?

Related Solutions

Recommended Content