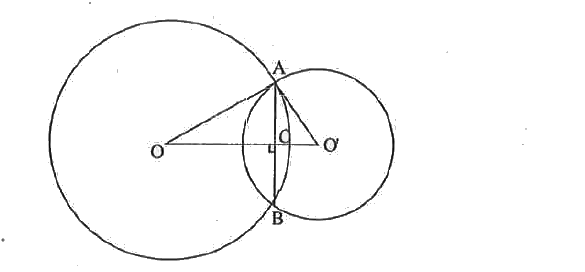
Two circles of radii 10 cm and 8 cm intersect each other and the length of common chord is 12 cm. The distance between their centres is .....A √7 cmB 3√7 cmC 4√7 cmD 8 + 2√7 cm
The correct option is: D 8 + 2√7 cmExplanation:M is the mid-point of AB .. AM = 6 cmAO r1 = 10 cm AO r2 = 8 cmAB is perpendicular to OO thenln ΔAOM 100 = 36 + OM2 [using pythagoras theorem]=> OM = 8 cm; In ΔAMO 64 = 36 + MO2 => √28 = MO => 2√7 MO. .. OO = 8 + 2√7 cm
Related Solutions
Two circles whose radii are 10 cm and 8 cm,intersect each other and their common chord is 12 cm long. What is the distance between their centres ?
View Solution10 cm. and 8 cm. Two circles of verbs intersect each other, and the length of the common chord is 12 cm. Is. Find the distance between their centres.
View SolutionTwo circles of radii 7 cm and 5 cm intersect each other at P and Q, and the distance between their centres is 10 cm. The length (in cm) of the common chord PQ is:
View SolutionIf the length of the transverse tangent is 8 cm, then calculate the centre distance (in cm) of the two circles with radii 7 cm and 3 cm.
View SolutionIf two circles of radii 7 cm and 3 cm touch each other extermally, then the distance between their centres will be 4 cm.
View SolutionTwo circles of radii 7 cm and 4 cm touch each other externally. Then the distance between their centres.
View SolutionTwo circles whose radii are 10 cm and 8 cm respectively, intersect each other at the points P and Q and their common chord is 12 cm in length. Find the distance between the centers of the two circles.
View Solution15 cm. and 12 cm. Two circles of radii intersect each other, and the length of their common chord is 18 cm. Is. What is the distance (in cm) between their centers?
View Solution10 सेमी तथा 8 सेमी त्रिज्या वाले दो वृत्त प्रतिच्छेद करते है। इनकी उभयनिष्ठ जीवा 12 सेमी है। उनके केंद्रों के बीच की दूरी ज्ञात कीजिए।
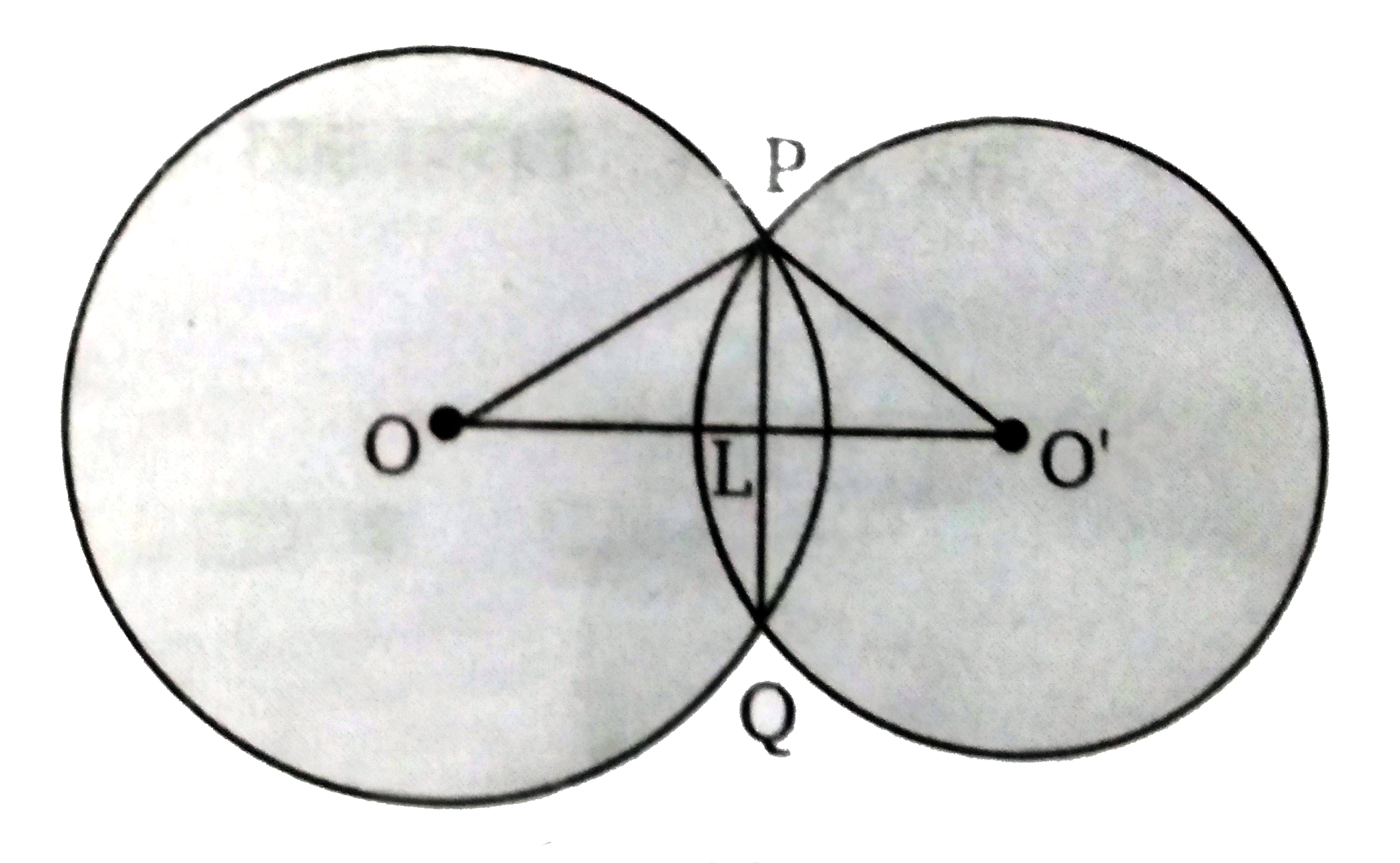
View SolutionTwo equal circles of radius 10 cm intersect each other and the length of their common chord is 12 cm . Find the distance between the centre of the circle .
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm, Find the length of the common chord.
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
View SolutionTwo circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
View SolutionJo's collection contains US, Indian and British stamps. If the ratio of US to Indian stamps is 5 to 2 and the ratio of Indian to British stamps is 5 to 1, what is the ratio of US to British stamps?
View Solution18 cm और 16 cm त्रिज्या वाले दो वृत्त एक दूसरे को प्रतिच्छेदित करते है और उनकी उभयनिष्ठ जीवा की लम्बाई 20 cm है | उनके केंद्रों के बीच की दूरी (cm में) ज्ञात करें |
View Solution10 সেমি এবং 8 সেমি ব্যাসার্ধবিশিষ্ট বৃত্তের দুটি পরস্পরকে ছেদ করেছে। তাদের সাধারন জ্যা-এর দৈর্ঘ্য 12 সেমি হলে বৃত্ত দুটির কেন্দ্রদ্বয়ের দূরত্ব কত?
View SolutionTwo each circles of radius 13 cm intersect each other and the length of their common chord is 10 cm. find the distance between the centre of the circle.
View SolutionThe radii of two circles with centres O and are 9 cm and 7 cm and the distance between their centres is 20 cm Then those circles will have _______ common tangents.
View SolutionThe distance between the centres of two circles having radii 8 cm and 3 cm, is 13 cm. The length (in cm) of the direct common tangent of the two circle is
View Solution