A tent is made in the form of a frustum of a cone surmounted by another cone. The diameter of the base and the top of the frustum are 20 m and 6 m respectively and the height is 24 m. If the height of the tent is 28 m and the radius of the conical part is equal to the radius of the top of the frustum find the quantity of canvas required. A 924.71 m2 B 1402.23 m2 C 1124.56 m2 D 1068.57 m2
The correct option is: D 1068.57 m2Explanation: Height of the cone part h1 = 28 - 24 = 4 m.Radius of base of the cone r1 = 6/2 = 3 mRadius of base of frustum r2 = 20/2 = 10 mHeight of the frustum h2 = 24 m Let l1 and l2 be the slant height of the cone and frustum respectively. So Quantity of canvas required = curved surface area of frustum + curved surface area of cone
Related Solutions
A tent is made in the form of a frustum of a cone surmounted by anoter cone. The diametere of the base top of the frustum are 20m and 6m respectvely, and the height is 24m. If the height of the tent is 28 m and the radius of the conical part is equal to the radius of the top of the frustum, fidn the quantity of can vas required. [ Take ]
View SolutionA tent is made in the form of a conic frustum surmounted by a cone . The diameter of the base and the top of the frustum are 20 m and 6m respectively and the height is 24 m . If the height of the tent is 28 m , find the quantity of canvas required ( Give your answer in ) .
View SolutionA tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m, the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent.
View SolutionA tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m, the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent.
View SolutionA tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m, the height of the frustum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent.
View SolutionA tent consists of a frustum of a cone, surmounted by a cone. If the diameters of the upper and lower and circular ends of the frustum be 14 m and 26 m respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of the canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of the surmounted conical portion are equal).
View SolutionFind the surface area of a frustum of a right circular cone with a slant height of 30 m, lower base radius 20 m and top radius of 15 m ?
View Solutionएक टेन्ट, एक शंकु के छिन्नक के आकार का है जिसका ऊपरी सिरा शंक्वाकार है। छिन्नक के आधार एवं शीर्ष के व्यास क्रमश : 14 m एवं 26 m हैं। यदि टेन्ट के छिन्नक की ऊंचाई 8 m और शंक्वाकार भाग की तिरछी ऊँचाई 12 m है, तो टेन्ट को बनाने का क्षेत्रफल ज्ञात कीजिए। (छिन्नक के ऊपरी सतह और शंकु के आधार की त्रिज्याओं को समान मानें)
View SolutionA tent consists of a frustum of a cone surmounted by a cone. If the diameter of the lower and upper circular ends of the frustum be 14 m and 26 m respectively, the height of the frustum be 8 m, and the slant height of the surmounted conical portion be 12m, find the area of canvas required to make the tent assuming the radii of the upper circular end and the base of surmounted conical portion are equal.
View Solutionएक तम्बू और एक शंकु को जोड़कर लंबवृत्तीय बेलन के रूप में बनाया जाता है। बेलन का व्यास 24 मी. है और बेलनाकार भाग की ऊँचाई 11 मी. है । जब कि शंकु का शीर्ष जमीन से 16 मी. ऊँचाई पर है। तम्बू में लगे हुए केनवास (कपड़े) का क्षेत्रफल ज्ञात कीजिए।
View SolutionA tent is shaped like a trunk of an elliptical cone. The upper end of which is conical. The diameter of the base and head of the incisor is 20 m and 6 m respectively. And the height is 24 m. If the total height of the tent is 28 m and the radius of the conical part is equal to the radius of the upper end of the frustum, find the area of the canvas used to make the tent. [ pi = 22//7 Take]
View SolutionA tent is in form of a cylinder of diameter 4.2 m and height 4 m surmounted by a cone of equal base and height 2.8 m. Find the capacity of the tent and the cost of canvas making the tent at ₹ 100 per square meter.
View Solutionशंकु के आकार का एक तंबू 10 m ऊँचा है और उसके आधार की त्रिज्या 24 m है | तंबू की तिर्यक ऊँचाई होगी :
View SolutionA tent of cloth is cylindrical up to 1 m height and conical above it of the same radius of base . If the diameter of tent is 6 m and the slant height of conical part is 5 m, find the cloth required to make this tent
View Solutionएक तम्बू को एक शकु रखकर शक्वाकार छिन्नक के रूप में बनाया जाता है | छिन्नक की ऊपरी और निचले सिरों के व्यास क्रमश : 20 मीटर और 6 मीटर तथा ऊचाई 24 मीटर है | यदि तम्बू की ऊचाई 28 मीटर हो तो केनवास का क्षेत्रफल ज्ञात कीजिए |
View SolutionThe volume of a conical frustum and that of a cylinder are same. The height of the cylinder is 1/3 m and radius is 62 m. The height of the frustum is 31 m and the radius of one end is 10 m. Find the radius of the other end.
View SolutionA tent is the form of a cylinder of diameter 15 m and height 2.4 m, surmounted by a cone of equal base and height 4 m. Find the capacity of the tent and the cost of the canvas at Rs. 50 per square metre.
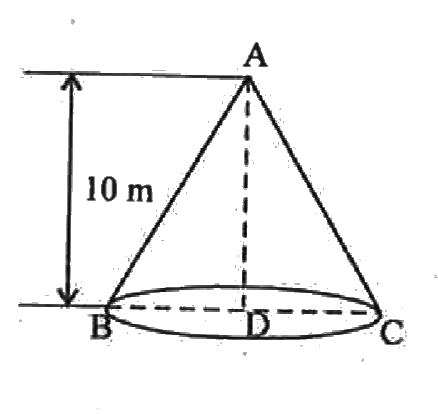
View SolutionA conical tent is 10 m high and the radius of its base is 24 m. Find slant height of the tent.
View SolutionA conical tent is 10 m high and the radius of its base is 24 m. Find slant height of the tent.
View SolutionA conical tent is 10 m high and the radius of its base is 24 m. Find
slant height of the tent.
 View Solution
View Solution
