A long smooth cylindrical pipe of radius r is tilted at an angle a to the horizontal Fig. 33. A small body at point A is pushed upwards along the inner surface of the pipe so that the direction of its initial velocity forms an angle φ with generatrix AB.Determine the minimum initial velocity v0 at which the body starts moving upwards without being separated from the surface of the pipe.
At any instant of time the complex motion of the body in the pipe can be represented as the superposition of two independent motions: the motion along the axis of the pipe and the motion in the circle in a plane perpendicular to the pipe axis Fig. 169. The separation of the body from the pipe surface will affect only the latter motion the body will not move in a circle. Therefore we shall consider only this motion. The body moving in a circle experiences the action of the normal reaction N of the pipe walls vector N lies in the plane perpendicular to the pipe axis and the force of gravity mg = mg cos α. We shall write the condition of motion for the body in a circle:where β is the angle formed by the radius vector of the point of location of the body at a given instant and the vertical y Fig. 170. For the body to remain in contact with the surface of the pipe the condition N = mv2/r — mg cos β ≥ 0 must be fulfilled whenceThe relation between the velocity v at which the body moves in a circle at a given instant andthe initial velocity v0 can be obtained from the energy conservation law: for any value of the angle β the following relation must hold:Substituting Eq. 3 into Eq. 2 we obtain the values of v0 for which the body remains in contact with the pipe:Since this condition must be satisfied for any value of β ∈ [0 2pi] we finally obtain
Related Solutions
A long smooth cylindrical pipe of radius r is tilted at an angle alpha to the horizotal (Fig). A small body at point A is pushed upwards along the inner surface of the pipe so that the direction of its initial velocity forms an angle varphi with generatrix AB. Determine the minimum initial velocity v_(0) at which the body starts moving upwards without being separated from the surface of the pipe.
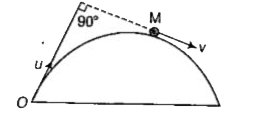
View SolutionA particle is projected from a point O with velocity u in a direction making an angle alpha upward with the horizontal. At P it is moving at right angle so its initial direction of projection. Its velocity at P is
View SolutionA particle is projected from a point O with velocity u in a direction making an angle alpha upward with the horizontal. AT P , it is moving at right angles to its initial direction of projection . Its velocity at P is .
View SolutionA particle is projected from a point O with velocity u in a direction making an angle alpha upward with the horizontal. AT P , it is moving at right angles to its initial direction of projection . Its velocity at P is .
View SolutionAn incompressible fluid flows steadily through a cylindrical pipe which has radius 2 R at point A and radius R at point B farther along the flow direction. If the velocity at point A is v, its velocity at point B is
View SolutionAn incompressible fluid flows steadily through a cylindrical pipe which has radius 2 R at point A and radius R at point B farther along the flow direction. If the velocity at point A is v, its velocity at point B is
View SolutionThere is a fixed semicircular ring of radius R lying in yz plane ,with centre at origin and it is uniformly charged with charge +Q A pipe is fixed along x-axis from the origin ,The inner surface is pipe is smooth and is made of insultaing material .A small ball of charge +q And mass m is projected in the pipe with negligible velocity ,ball can move in the pipe whole arrangement is in gravity free space. Normal reaction exerted by pipe on ball when the ball is moving in pipe is along
View SolutionA ball of radius 1 cm is put into a cylindrical pipe so that it fits inside the pipe. If the length of the pipe is 14 m, what is the surface area of the pipe?
View SolutionAn incompressible fluid flows steadily through a cylindrical pipe which has radius 2R at point A and radius R at point B. Further, along the flow direction, if the velocity at point A is v, its velocity at point B will be
View SolutionR radius and uniform surface charge density sigma carrier slender long insulator cylindrical pipe, having a constant angular velocity omega is rotating about its axis. The energy density of the magnetic field inside the pipe is:
View Solutionएक पिण्ड चित्रानुसार बिन्दु O से u वेग से क्षैतिज से कोण बनाते हुए प्रक्षेपित लिया जाता है। किसी बिन्दु M पर यह प्रारम्भिक प्रक्षेपण दिशा से समकोण पर स्थित है। M पर इसका वेग है
 View Solution
View Solutionएक पिण्ड चित्रानुसार बिन्दु O से u वेग से क्षैतिज से कोण बनाते हुए प्रक्षेपित किया जाता है। किसी बिन्दु M पर यह प्रारम्भिक प्रक्षेपण दिशा से समकोण पर स्थित है। M पर इसका वेग है
 View Solution
View SolutionA body is projected upwards. What is its initial velocity at maximum height?
View SolutionA particle is projected from a point O with a velocity u at an angle (upwards) to the horizontal. At a certain point P it moves at right angles to its initial direction. It follows that:
View Solutionएक कण प्रारंभिक वेग g मी/से उर्ध्वार्धर दिशा में ऊपर की और फेका जाता है। कण द्वारा तय की गई महत्तम ऊंचाई है
View SolutionThe area of curved surface of the outer and inner surface of a hollow funnel shaped pipe is 44 sq. Cm and the length of the pipe is 14 cm. The metal of the pipe is 99 cubic centimeters. Determine the outer and inner radius of the pipe.
View SolutionA body is projected vertically upwards from the surface of a planet of radius with a velocity equal to hall the escape velocity for that planet. The maximum height attained by the body is
View SolutionA body is projected vertically upwards from the surface of a planet of radius with a velocity equal to half the escape velocity for that planet. The maximum height attained by the body is
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to half the escape velocity for that planet. The maximum height attained by the body is
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to 1/3rd the escape velocity for the planet. The maximum height attained by the body is
View Solution
