Show that ∇ × f vector F = ∇Q × vector F + ∇ × vector f.

Consider a vecotor vector F = 4hati - 3hatj . What is the vector perpendicular to F?

View Solution

f $\vec{a}$ is any vector , then -

View Solution

एक सदिश $\vec{F} = 4 \hat{i} - 3 \hat{j}$ है। इस सदिश के लम्बवत् सदिश होगा

View Solution

Pressure is a vector quantity. (T or F)

View Solution

Consider a vector $\vec{F} = 4 \hat{i} - 3 \hat{j}$ . Another vector that is perpendicular to $\vec{F}$ is

View Solution

Consider a vector $\vec{F} = 4 \hat{i} - 3 \hat{j}$ . Another vector that is perpendicular to $\vec{F}$ is

View Solution

Consider a force vector F=hati+ hatj + hatk Another vector perpendicular to F is

View Solution

Assertion: Pressure is a vector quantity. Reason: Pressure P=(F)/(A) . Here F , the force is a vector quantity.

View Solution

Assertion: Pressure is a vector quantity.
Reason: Pressure $P = \frac{F}{A}$ . Here $F$ , the force is a vector quantity.

View Solution

Which of the figure's six arrangements correctly show the vector addition of forces ${\vec{F}}_{1}$ and ${\vec{F}}_{2}$ to yield the third vector, which is meant to represent their net force ${\vec{F}}_{net}$ ?
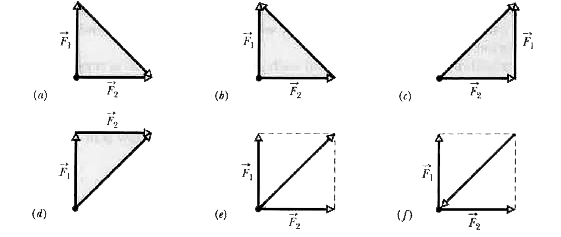ocr_image

View Solution

कारण सहित बताइए कि अदिश तथा सदिश राशियों के साथ क्या निम्नलिखित बीजगणितीय संक्रियाएँ अर्थपूर्ण हैं ?
(f ) एक सदिश के घटक को उसी सदिश से जोड़ना ।

View Solution

ਕਾਰਨ ਸਮੇਤ ਦੱਸੋ ਕਿ ਅਦਿਸ਼ ਅਤੇ ਸਦਿਸ਼ ਰਾਸ਼ੀਆਂ ਨਾਲ ਹੇਠ ਲਿਖੀਆਂ ਬੀਜਗਣਿਤਿਕ ਕਿਰਿਆਵਾਂ ਅਰਥ-ਪੂਰਨ ਹਨ? (f) ਇੱਕ ਸਦਿਸ਼ ਦੇ ਘਟਕ ਨੂੰ ਉਸੇ ਸਦਿਸ਼ ਨਾਲ ਜੋੜਨਾ

View Solution

Let the unit vectors vec a,vec b,vec c be the position vectors of the vertices of a Delta ABC. If F is the position vector of the mid point of line segment joining its orthocenter and centroid, then (vec a-vec F)^(2)+(vec b-vec F)^(2)+(vec a-vec F)^(2)

View Solution

Let $f : Q \to Q : f (x) = 3 x - 4$ show tha t f is invertible and find $f^{- 1}$

View Solution

Assertion: $\vec{τ} = \vec{r} \times \vec{F}$ and $\vec{τ} \neq \vec{F} \times \vec{r}$
Reason: Cross product of vectors is commutative.

View Solution

एक बल F एक कण P पर चित्रानुसार लगाया गया है। यहाँ, r कण का स्थिति सदिश है।
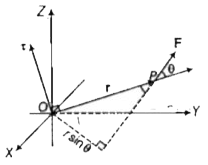
ocr_image
F की दिशा लम्बवत् होनी चाहिए

View Solution

If V be the vector spacce of all functions from R to R and W-{f:2f(3)=f(1)}

View Solution

Consider a force vector F=hati+ hatj + hatk Anorther vectoer perpendicular of F is

View Solution

Consider vec(F)=4hat(i) - 3hat(j) . A vector perpendicular to vec(F) is :

View Solution

If $θ$ is smaller angle between force vector $\vec{F}$ and velocity vector $\vec{v}$ then Fv cos $θ$ represents

View Solution

Show that ∇ × f vector F = ∇Q × vector F + ∇ × vector f.

By definition

Related Solutions

Recommended Content