The Dowlaiswaram Anicut is an important canal system in the a Godavari Delta b Krishna Delta c Ganga Delta d Cauvery Delta
a Godavari Delta
Related Solutions
If ,than relative error in Z is equal to
(a)
(b)
(c)
(d)
View SolutionOn which coastal plain are the deltas of the Godavari, Mahandi , Krishna and Kaveri formed?
View Solutionकृष्णा एवं गोदावरी नदी का डेल्टा किस राज्य में पड़ता है?
View SolutionName the fossil fuel which is mostly found in Tripura, Rajasthan, Maharashtra and in Krishna Godavari delta.
View Solution(A) : If , then the percentages error in the measurement of x,
(R) : The above is true for all values of .
View SolutionIn a triangle is equal to (b) (d)
View SolutionIn a triangle is equal to (b) (d)
View Solutionब्रह्मपुत्र, गोदावरी तथा ताप्ती में से कौन-सी नदी का. मुहाना (डेल्टा) नहीं है?
View SolutionIn the figure, and . Prove that is an isosceles triangle.
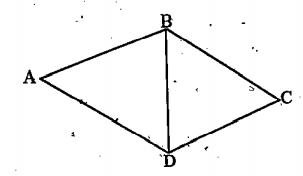
View SolutionIf a, b, c are sides of a triangle and , then name the type of triangle. a) Obtuse angled triangle b) Acute angled triangle c) Right angled triangle d) Equilateral triangle
View SolutionProve the
View Solution………… The city is situated on the delta of the Krishna River.
View Solutionis an equilateral triangle formed on a side of a square Show that .
View SolutionWhich is the northernmost point of the Ganga Delta?
View SolutionIf , then
a) b) c) d)
View SolutionA(-4,0),B(4,0) and C(0,3) are the vertices of _-
a)an Equilateral triangle b)an Isosceles triangle c)a Right angled triangle d)a Scalane triangle
View SolutionIf triangle is similar to triangle such that and area of triangle . Determine the area of triangle
View SolutionIf one angle of a triangle is equal to the sum of the other two angles, then the triangle is (a) an isosceles triangle (b) an obtuse triangle (c) an equilateral triangle (d) a right triangle
View SolutionIf the medians of a intersect at show that . GIVEN : such that its medians and intersect at TO PROVE : .
View SolutionIf the medians of a intersect at show that . GIVEN : such that its medians and intersect at . TO PROVE :
View Solution