A spring of mass M and spring constant k is hanged from a rigid support. A mass m is suspended at the lower end of the spring. If the mass is pulled down and released then it will execute SHM. Find the frequency of oscillations.
Let l be the length of the coiled wire of the spring. Let the suspended mass m be at a distance z from the equilibrium position. We consider an element of length dx of the spring situated between points x and x + dx measured along the spring from the point of support. Since the stretching is assumed to be uniform the element distant x from the fixed end will experience a displacement x/l z and will have velocity b g xl z&. Since the mass of the element dx is M/l zdx the kinetic energy of this element is.Thus at that instant total kinetic energy of the spring isand the kinetic energy of the mass m is The potential energy of the system when the spring is elongated by z is 1/2 kz2.Hence the total energy of the system isDue to finite mass of the spring the effective mass of the system becomes m +M/3. From problem 46 we find that Differentiating Eqn. 1.19 with respect to t we obtainwhich shows that the motion is simple harmonic with ω2 given by Eqn. 1.20.
Related Solutions
a mass m is suspended at one end of a spring and the other end of the spring is fimly fixed on the celling. if the mass is slightly depressed and released it will execute oscillation. write down the expression for the frequency of oscillation of the mass.
View SolutionAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
View Solutionएक m द्रव्यमान का गुटका स्प्रिंग नियतांक k की स्प्रिंग से ऊर्ध्वाधर रूप से लटक रहा है। यदि द्रव्यमान को ऊर्ध्वाधर रूप से दोलन कराया जाता है, तो इसकी कुल ऊर्जा होती है
View Solutionबल-नियतांकों के दो स्प्रिगों को लम्बाई में जोड़ कर ऊर्ध्वाधर लटकाया गया है स्प्रिंग के निचले सिरे पर m द्रव्यमान का एक पिण्ड लटका दिया गया है। स्प्रिंग के कम्पन का दोलनकाल ज्ञात कीजिए।
View SolutionA object of mass m is suspended from a spring and it executes SHM with frequency n. If the mass is increased 4 times , the new frequency will be
View SolutionA object of mass m is suspended from a spring and it executes SHM with frequency n. If the mass is increased 4 times , the new frequency will be
View SolutionAn ideal spring with spring constant k is suspended from the ceiling, and a block of mass M is attached to its lower end. If the mass is released initially when the spring is not stretched, then the maximum extension in the spring is:
View SolutionA block with a mass of is suspended from an ideal spring having negligible mass and stretches the spring by .
(a) What is the force constant of the spring?
(b) What is the period of oscillation of the block if it is pulled down and released ?View SolutionA block with a mass of 3.00 kg is suspended from an ideal spring having negligible mass and stretches the spring by 0.2 m . (a) What is the force constant of the spring? (b) What is the period of oscillation of the block if it is pulled down and released ?
View SolutionA block with a mass of 3.00 kg is suspended from an ideal spring having negligible mass and stretches the spring by 0.2 m . (a) What is the force constant of the spring? (b) What is the period of oscillation of the block if it is pulled down and released ?
View SolutionA spring of spring constant 'k' is supported from one end and tied by a mass 'm' at the other end. Write the formula to find the period of oscillation of the mass body. (Ignore the mass of the spring).
View SolutionThe period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionA mass hangs at the end of a massless spring and oscillates up and down at its natural frequency f. If the spring is cut at the midpoint and and mass reattached at the end, the frequency of oscillation is :
View Solution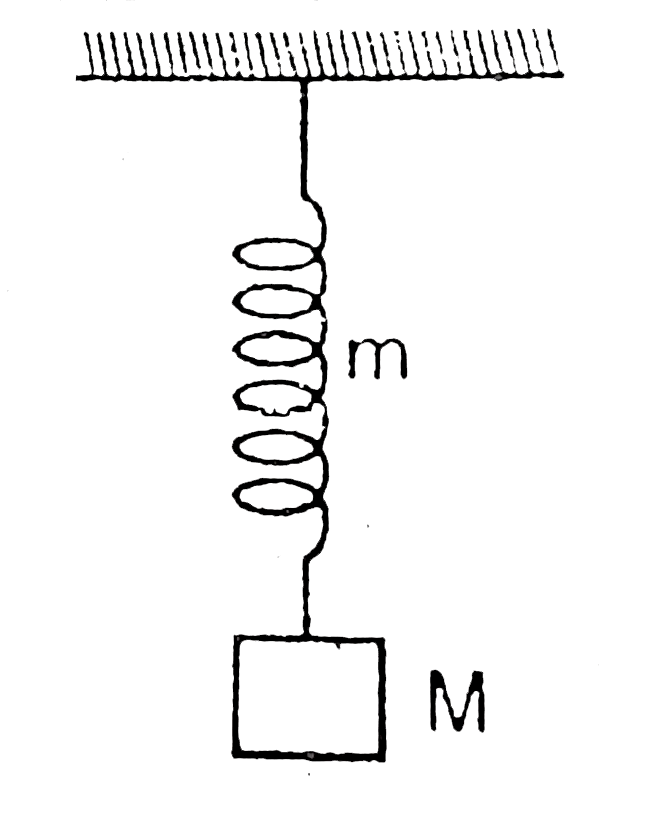
A block of is suspended from a vertical spring of mass as shown in the figure. When block is pulled down and released the mass oscillates with maximum velocity .View Solutionबल नियतांक K वाली एक स्प्रिंग से लटके द्रव्यमान m का दोलनकाल T है | यदि स्प्रिंग का एक - चौथाई भाग काटकर अलग कर दिया जाता है तो शेष स्प्रिंग से दोगुना द्रव्यमान लटकाने पर उसका दोलनकाल होगा :
View SolutionA body of mass 1 kg suspended by a light vertical spring of spring constant 100 N/m executes SHM. Its angular frequency and frequency are
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA weightless spring which has a force constant k oscillates with frequency n when a mass m is suspended from it The spring is cut into two equal halves and a mass 2m is suspended from it. The frequency of oscillation will now become
View SolutionA massless spring, having force constant k, oscillates with a frequency n when a mass m is suspended from it. The spring is cut into two equal halves and a mass 2m is suspended from one of the parts. The frequency of oscillation will now be………….
View Solution
