The potential energy of a particle of mass m is given byVx = a/x2 -b/x where a and b are positive constants. Find the minimum of Vx and expand Vx about the point of minimum of Vx. Find the period of small oscillations that the particle performs about the position of minimum of Vx.
If we put y = x – 2a/b the equation of motion about the position of minimum of Vx is
Related Solutions
निम्नांकित क्यों अर्थहीन है?
VX
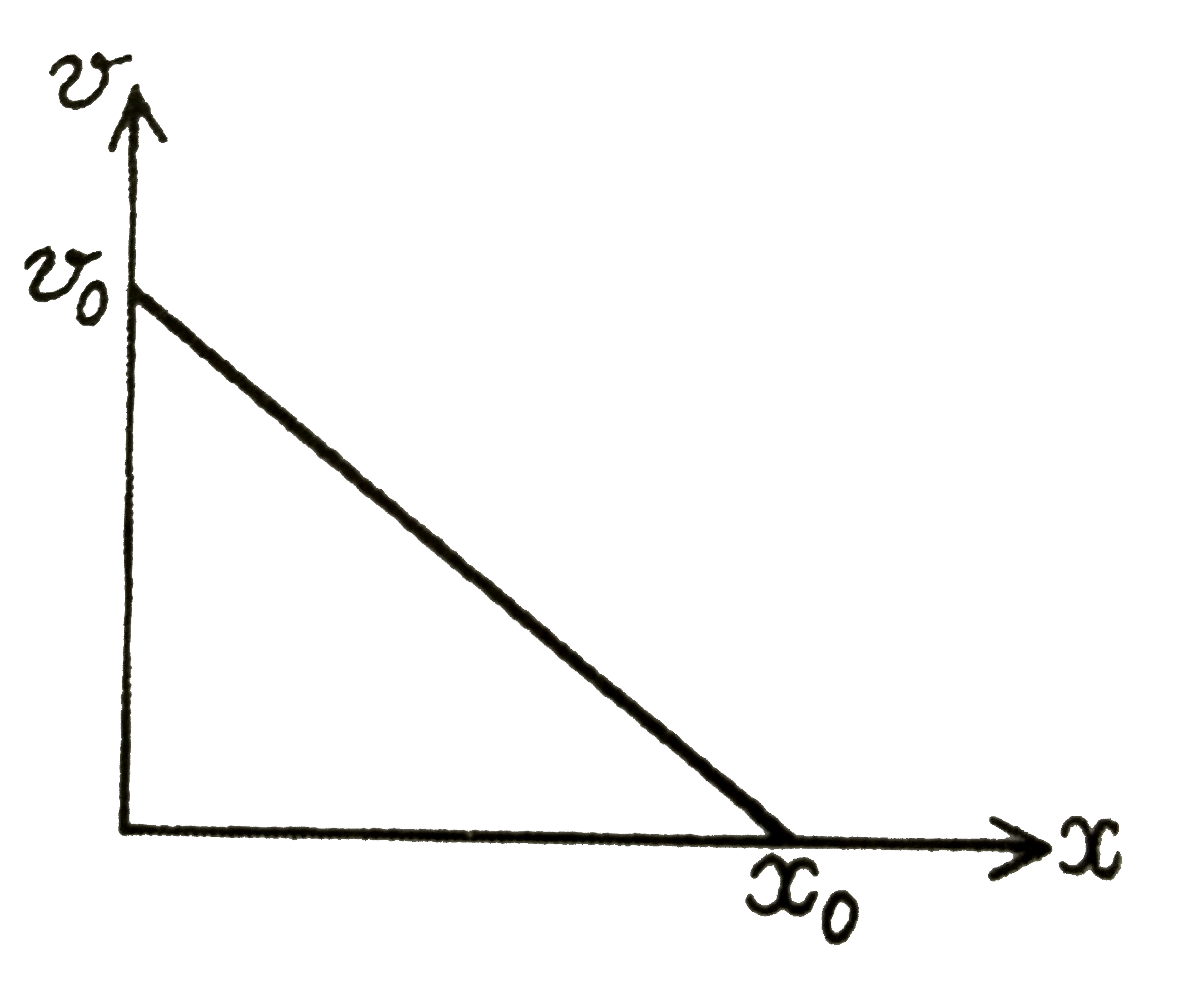
View Solutionएक सीधी रेखा के अनुदिश गतिमान कण का वेग -दूरी (v-x) ग्राफ संलग्न चित्र में दिखाया गया है । निम्नांकित में से कौन-सा त्वरण दूरी (a-x) ग्राफ दिये गये वेग-दूरी ग्राफ दिये गये वेग-दूरी (v-x) ग्राफ के संगत है ?
View Solutionwhere
View SolutionThe velocity-distance (vx) graph of a particle moving along a straight line is shown in the attached figure, which of the following acceleration-distance (ax) graphs correspond to the given velocity-distance (vx) graphs.
View SolutionWhich of the following is not meaningful? (a) XIV (b) XXXV (c) XXV (d) VX
View SolutionWhich of the following is not meaningful? XIV (b) XXXV (c) XXV (d) VX
View SolutionIf f(x)=max(sin x,cos x) Vx e R. Then sum ofmaximum and minimum values of f(x) is M then find (1)/(M+(1)/(sqrt(2)))
View SolutionSelect the related word/letters from the given alternatives. TR : VX :: MK : ?
View SolutionThe transformation reduces to
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=-ax^2+bx^4 , where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=-ax^2+bx^4 , where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA particle of mass m moves in a one dimensional potential energy , where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionThe differential equation of the family curves, where a, b, c are arbitrary constants, is :
View SolutionA particle of mass m is located in a one dimensional potential field where potential energy of the particle has the form u(x) = a/x^(2)-b/x) , where a and b are positive constants. Find the period of small oscillations of the particle.
View SolutionA particle of mass m is free to move along x axis under the influence of a conservative force. The potential energy of the particle is given by U=-ax^(x) e^(-bx) [a and b are positive constants] Find the frequency of small oscillations of the particle about its equilibrium position
View SolutionThe potential energy of a peticle of mass 'm' situated in a unidimensional potential field varies as U(x) = 0 [1 - cos ax] , where U_(0) and a are constants. The time period of small oscillations of the particle about the mean positions is :
View SolutionThe potential energy of a peticle of mass situated in a unidimensional potential field varies as , where and a are constants. The time period of small oscillations of the particle about the mean positions is :
View Solutionनिम्नलिखित में से कौन-सी शिक्षण-अधिगम व्यूह रचना (कौशल) सृजनात्मकता में बाधा पहुँचाती है ?
View SolutionTrue or false:
A homogenous differntial equation can be solved by the substitution .
View SolutionXXXX, VX, IC, XW are not written. Can you tell why?
View Solution