Derive an expression for the torque acting on an electric dipole which is held in a uniform electric field when the axis of the dipole makes an angle q with the electric field.
Consider an electric dipole placed in a uniform electric field of strength E in such a way that its dipole moment vector p makes an angle q with the direction of vector E. The charges of dipole are - q and + q at separation 2l the dipole moment of electric dipole p = q.2l ...1 Force: The force on charge + q is vector F1 = q vector E along the direction of field vector E The force on charge - q is vector F2 = qE opposite to the direction of field vector E Obviously forces vector F1 and F2 are equal in magnitude but opposite in direction; hence net force on electric dipole in uniform electric field is F = F1 - F2 = qE - qE = 0 zero As net force on electric dipole is zero so dipole does not undergo any translatory motion. Torque: The forces vector F1 and vector F2 form a couple or torque which tends to rotate and align the dipole along the direction of electric field. This couple is called the torque and is denoted by τ. ∴ torque τ = magnitude of one force ´ perpendicular distance between lines of action of forces = qE BN = qE 2lsinθ =q 2l Esinθ = pEsinq [usinθ1] ....2 Clearly the magnitude of torque depends on orientation θ of the electric dipole relative to electric field. Torque τ is a vector quantity whose direction is perpendicular to both vector p and vector E . In vector form vector τ = vector p x vector E ...3 Thus if an electric dipole is placed in an electric field in oblique orientation it experiences no force but experiences a torque. The torque tends to align the dipole moment along the direction of electric field. Maximum Torque: For maximum torque sinθ should be the maximum. As the maximum value of sin q =1 when θ = 90° ∴ Maximum Torque τmax = pE
Related Solutions
Derive the expression for the torque acting on an electric dipole, when it is held in a uniform electric field. Identify the orientation of the dipole in the electric field, in which it attains stable equilibrium.
View SolutionDerive an expression for the torque acting on an electric dipole placed in a uniform electric field.
View SolutionDerive an expression for torque acting on an electric dipole in uniform electric field.
View SolutionDefine the term electric dipole moment. Give its units Derive an expression for the maximum torque acting on an electric dipole, when held in a uniform electric field.
View SolutionDerive an expression for torque acting on an electric dipole suspended in a uniform electric field. Use this relation to derive the expression for P.E. of dipole in an electric field.
View SolutionDerive an expression for torque acting on an electric dipole in a uniform two dimensional electric field.
Or
Write the expression for torque acting on a dipole of dipole moment placed in an electric field .View SolutionDerive the expression for torque on an electric dipole in a uniform electric field.
View SolutionDerive the expression for torque on an electric dipole placed in a uniform electric field.
View SolutionDerive an expression for torque experiencedby electric dipole in a uniform electric field
View SolutionDerive an expression for torque experiencedby electric dipole in a uniform electric field
View SolutionObtain the expression of torque acting on electric dipole in uniform external electric field.
View SolutionFind an expression for torque acting on an electric dipole placed in a uniform electric field.
View SolutionAn electric dipole is placed in a uniform electric field of Intensity E as shown in the figure.
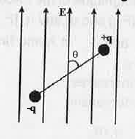 Copy the diagram, mark the forces and derive an expression for torque.View Solution
Copy the diagram, mark the forces and derive an expression for torque.View SolutionFind the expression of torque acting on an electric dipole placed in a uniform electric field . Using the above obtained expression of torque find the expression for potential energy of electric dipole kept in the uniform electric field . Assume potential energy of electric dipole to be zero when its axis is perpendicular to the externally applied electric field .
View SolutionWhen an electric dipole is held at an angle in a uniform electric field, the net force F and torque on the dipole are
View SolutionWhen an electric dipole is held at an angle in a uniform electric field, the net force F and torque tau on the dipole are
View SolutionDerive an expression for the torque acting on an electric dipole suspended freely in a uniform electric field. How will you determine the direction of torque?
View SolutionDerive a expression for the torque acting on a electric dipole in uniform electric field. Under what condition, the torque will be maximum?
View SolutionDerive an expression for couple acting on an electric dipole kept in a uniform electric field.
View SolutionDerive the expression for the couple acting on the electric dipole in uniform electric field
View Solution
