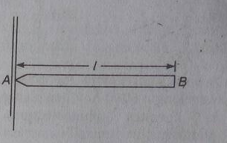
A rod with length l rotates about support A with angular position given by ϕt = κ t2 . A body G slides along the rod with position rt = l1 − κ t2 . a Find the magnitude of velocity and acceleration of G when ϕ = 45◦ . b At what angle ϕ does G hit the support? Given: l = 2 m κ = 0.2 s−2
a First we calculate the time t = t1 that it takes the rod to reach the position ϕ = ϕ1 = 45◦:Then we determine the derivatives of the given functions rt and ϕt:and the accelerationb Body G reaches the support r = 0 at time tE:This yields the corresponding angle ϕE
Related Solutions
Suppose A is the set of students in your class who were absent on Tuesday and B the set of students who were absent on Wednesday. Then, A = {Roja, Ramu, Ravi} and B = {Ramu, Preethi, Haneef} Now, we want to find K, the set of students who were absent on either Tuesday or Wednesday. Then, does Roja in Κ? Ramu in Κ? Ravi in Κ? Haneef in Κ? Preeti in Κ? Akhila in Κ?
View SolutionA uniform rod of length (in between the supports) and mass is placed on two support and . The rod breaks suddenly at length from the support . Find the reaction at support immediately after the rod breaks

View SolutionA unifrom rod of length and mass is free to rotate in a vertical plane about , Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
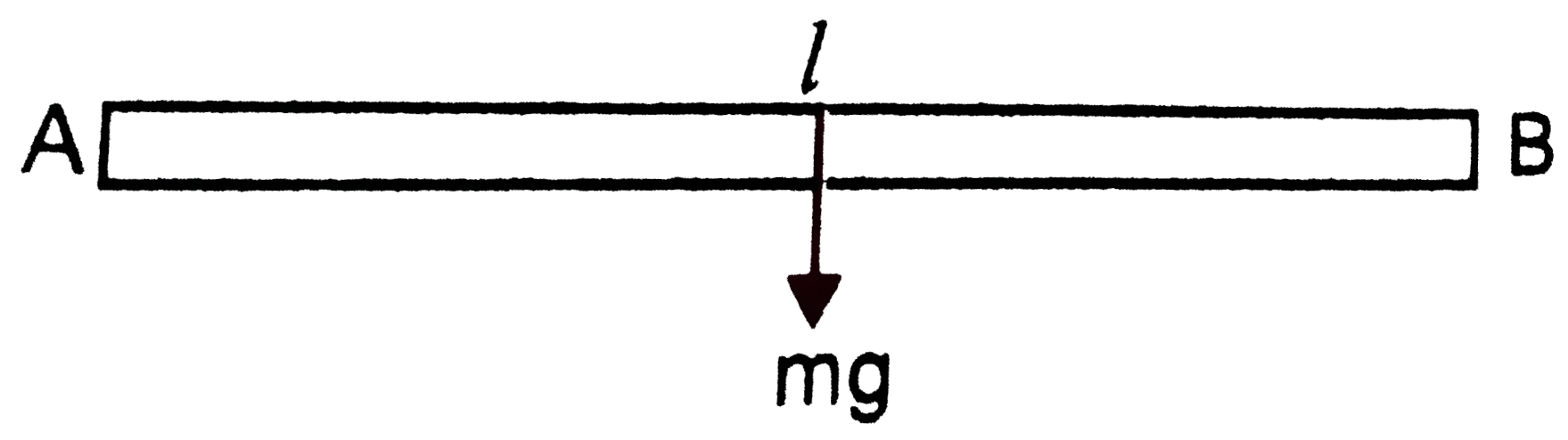
View SolutionA unifrom rod of length l and mass m is free to rotate in a vertical plane about A , Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is (MI "of rod about" A "is" (ml^(2))/(3))
View SolutionA uniform rod of length L(in between the supports) and mass mis placed on two supports A and B. The rod breaks suddenly at length L/10 from the support B. Find the reaction at support A immediately after the rod breaks
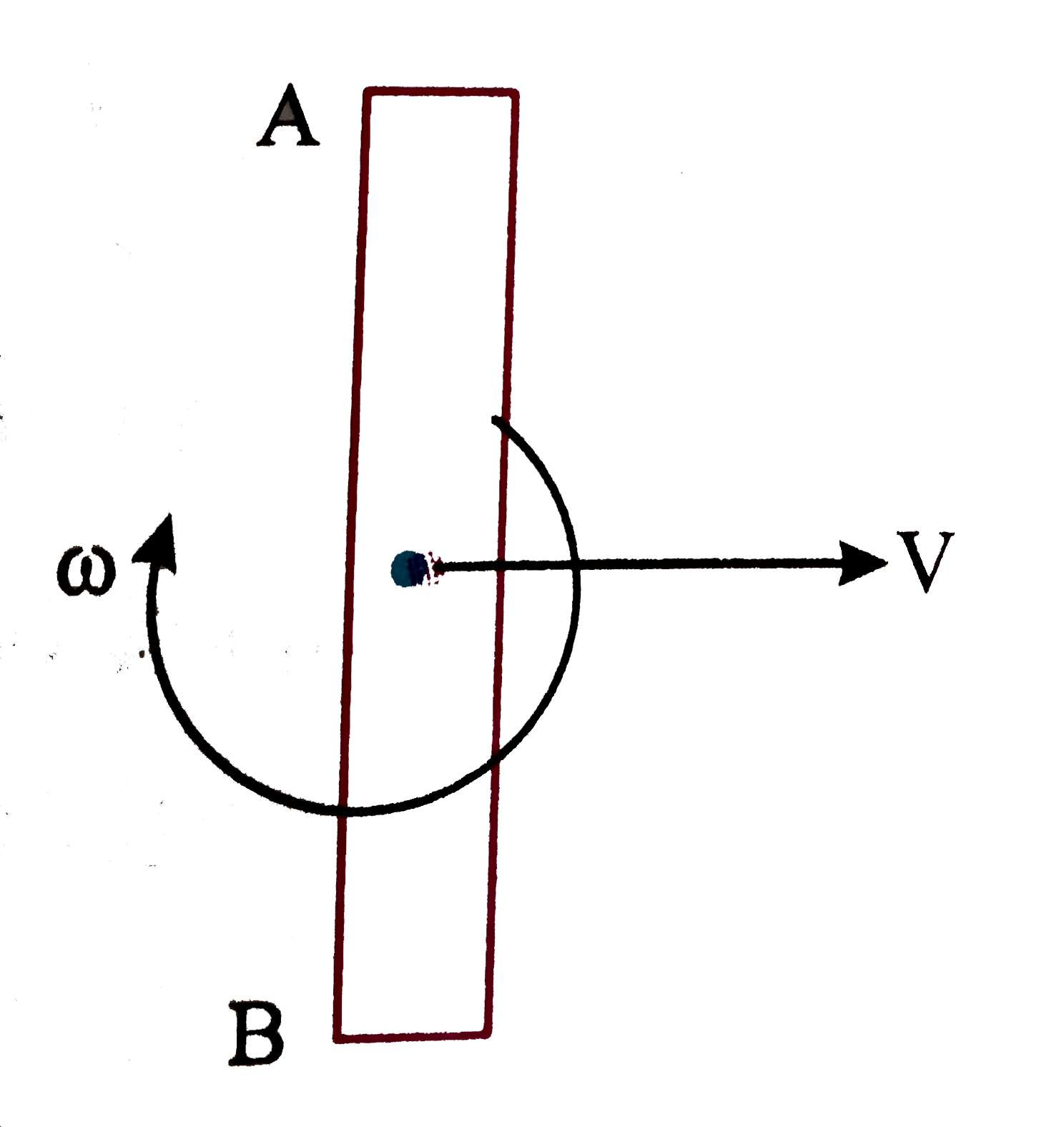
View SolutionA rod of length is travelling with velocity and rotating with angular velocity such that . The distance travelled by end of the rod when rod rotates by an angle is
View SolutionA rod of mass 100 g and length 1.0 m makes an angle with the axis passing through its centre. Find (i) the moment of inertia of the rod about the give axis. (ii) If the rod rotates with an angular velocity of 2.0 rad about the given axis find the rotational kinetic energy of the rod.
View Solutionएक समरूप छड़ AB की लम्बाई l तथा द्र्वयमान m है , यह बिंदु A के परित घूर्णन के लिए स्वतंत्र है । क्षैतिज स्थिति में विराम से छड़ को छोड़ा जाता है । छड़ का A के परित : जड़त्व आघूर्ण हो तब का प्रारम्भिक कोणीय त्वरण होता -

View SolutionA uniform rod of length l is released from the position shown in the figure. The acceleration due to gravity is g . There is no friction at any surface. Find the initial angular acceleration of the rod.
View SolutionA rod of length l and total charge 'q' which is uniformly distributed is rotating with angular velocity omega about an axis passing through the centre of rod and perpendicular to rod. Find the magnitude of magnetic dipole moment (in Amp. m^(2) ) of rod. If q=4C, omega=3rad//s and l=2m
View SolutionA rod of length and total charge which is uniformly distributed is rotating with angular velocity about an axis passing through the centre of rod and perpendicular to rod. Find the magnitude of magnetic dipole moment (in Amp. ) of rod. If and
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is , the initial angular acceleration of the rod will be

View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is , the initial angular acceleration of the rod will be
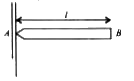
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is , the initial angular acceleration of the rod will be

View SolutionA unifrom rod AB of length l,and mass m is free to rotate about point A.The rod is release from rest in the horizontal position Given that the moment of inertia of the rod about A is , the initial angular acceleration of the rod will be:
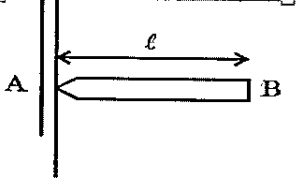
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is , the initial angular acceleration of the rod will be
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is , the initial angular acceleration of the rod will be

View SolutionA unifrom rod of length and mass is free to rotate in a vertical plane about as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA uniform rod of length and mass is free to rotate in a vertical plane about as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:
View Solution