Two pendulum bobs of unequal mass are suspended from the same fixed point by strings of equal length. The lighter bob is drawn aside and then released so that it collides with the other bob on reaching the vertical position. The collision is elastic. What quantities are conserved in the collision? A. Both kinetic energy and angular momentum of the system B. Only kinetic energy C. Only angular momentum D. Angular speed of lighter bob E. None of the above
A. Both kinetic energy and angular momentum of the system
Related Solutions
Which of the following statements is false for collisions-
(1)Momentum is conserved in elastic collisions but not in inelastic collisions.
(2)Total-kinetic energy is conserved in elastic collisions but momentum is not conserved.
(3)Total kinetic energy and momentum both are conserved in all types of collisions
(4)Total kinetic energy is not conserved in inelastic collisions but momentum is conserved
View SolutionEffective length of a pendulum is 50 cm and the mass of the bob is 4g . The bob is drawn to one side until the string is horizontal , and is then released. When the string makes an angle with the vertical , what is the velocity and the kinetic energy of the bob ?
View SolutionMass of the bob of a pendulum is 100g and the length of the string is 1m . The bob is initially held is such a way that the string is horizontal . The bob is then released. Find the kinetic energy of the bob when the string makes an angle of (ii) 30^@ with the vertical .
View SolutionMass of the bob of a pendulum is 100g and the length of the string is 1m . The bob is initially held is such a way that the string is horizontal . The bob is then released. Find the kinetic energy of the bob when the string makes an angle of (i) 0^@ with vertical
View SolutionEffective length of a simple pendulum is 50 cm and mass of the bob suspended is 4 g. The bob is pulled to one side to make the string horizontal and then it is released. What will be the kinetic energy of the bob when it makes an angle 60^(@) with the vertical?
View SolutionThe bob of a pendulum of length 980 cm is released from rest with it string making an angle 60^(@) with the vertical. It collides with a ball 20g resting on a smooth horizontal surface at the position of rest of pendulum. If the collision is perfectly elastic, with what velocity will the bob move immediately after the collision ? Mass of the bob is 10g
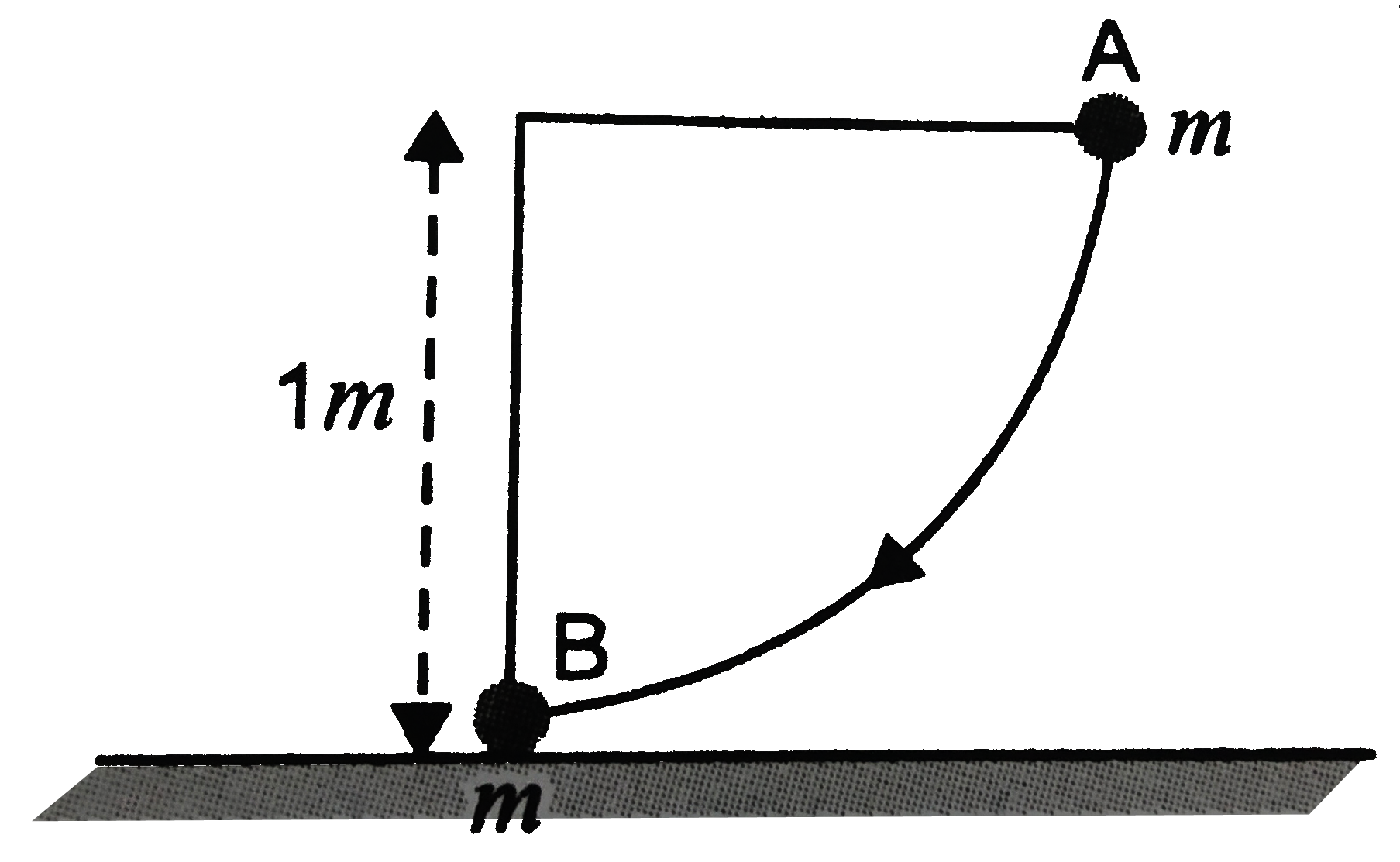
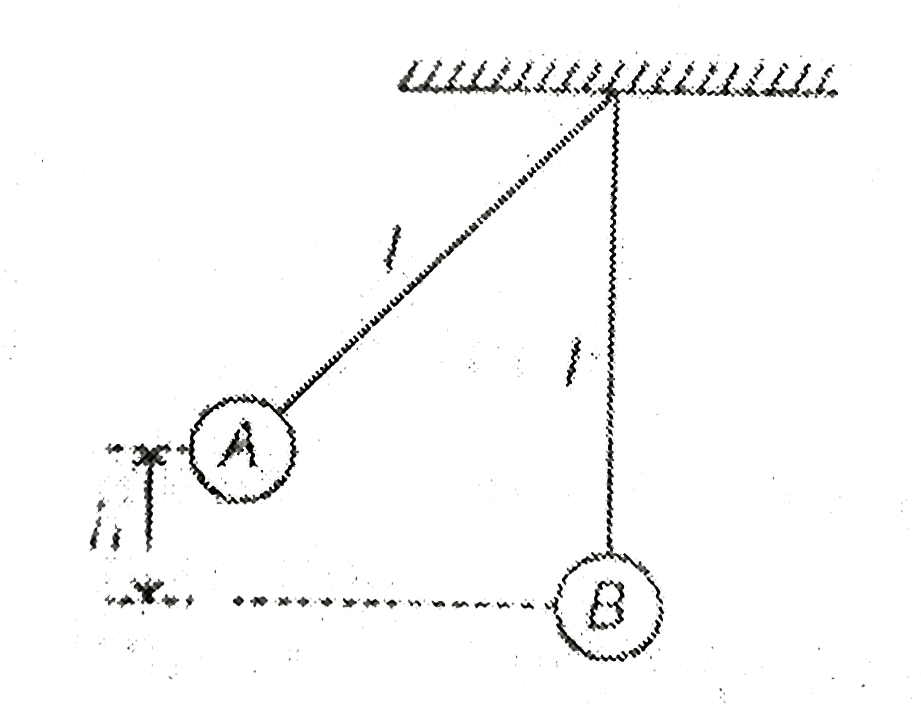
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob will rise after collision.
(b) the speed with which bob starts moving.
Neglect the size of the bobs and assume the collision to be elastic.
View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
If the length of the pendulum is 1m, calculate
(a) the height to which bob will rise after collision.
(b) the speed with which bob starts moving.
Neglect the size of the bobs and assume the collision to be elastic.

View SolutionThe bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure. If the length of the pendulum is 1m, calculate (a) the height to which bob A will rise after collision. (b) the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
View SolutionThe bob A of a pendulum released from to the vertical hits another bob B of the same mass at rest on a table as shown in figure . How high does the bob A rise after the collision ? Neglect the size of the bobs and assume the collision to be elastic .
View SolutionA simple pendulum bob has a mass ''m'' and length ''L'' . The bob is drawn aside such that the string is horizontal and then it is released. The velocity of the bob while it crosses the equilibrium position is
View SolutionThe mass of a simple pendulum bob is 100 gm. The length of the pendulum is 1 m. The bob is drawn aside from the equilibrium position so that the string makes an angle of 60^(@) with the vertical and let go. The kinetic energy of the bob while crossing its equilibrium position will be
View SolutionIn the 1st figure shown here rod is massless and at its end a bob of mass m is attached. The other figure is a uniform rod also of mass m. As they are released, at the bottom

A. The bob has higher kinetic energy but lower angular velocity
B. The bob has higher kinetic energy as well higher angular velocity
C. The bob has lower kinetic energy but higher angular velocity
D. The bob has lower kinetic energy as well lower angular velocity
View SolutionIn non-elastic collision, both momentum and kinetic energy are conserved.
View SolutionTwo identical simple pendulums A and B are fixed at same point. They are displaced by very small angles alpha " and " beta ( = 2 alpha) respectively and are simultaneously released from rest at time t = 0. Collisions between the pendulum bobs are elastic and length of each pendulum is l. (a) What is the minimum number of collisions between the bobs after which the pendulum B will again reach its original position from where it was released ? (b) Find the time (t) at which B reaches its initial position for the first time after the release. (c) Write the kinetic energy of pendulum B just after n^(th) collision? Take mass of each bob to be m.
View SolutionMass of the bob of a simple pendulum is 10g and the effective length is 13 cm. The bob is pulled 5 cm away from the vertical and then released. What will be the kinetic energy of the bob when it passes through the lowest point?
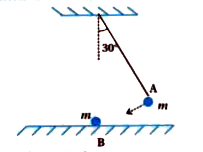
View SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
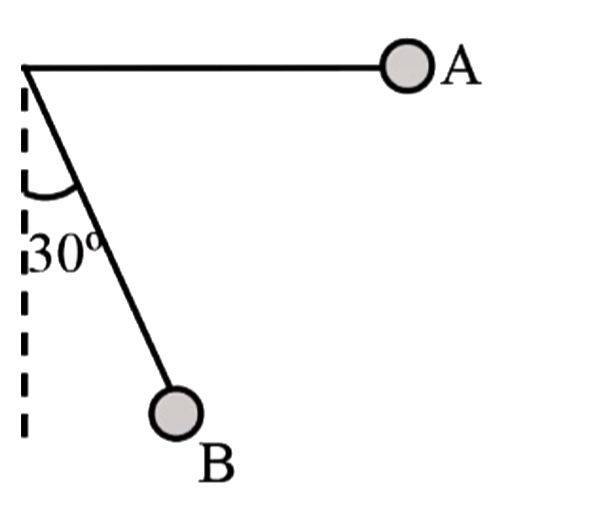
View SolutionA simple pendulum is released from A as shown. If m and 1 represent the mass of the bob and length of the pendulum, the gain kinetic energy at B is
View SolutionA simple pendulum is released from A as shown. If m and l represent the mass of the bob and length of the pendulum, the gain in kinetic energy at B is
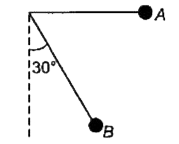
View SolutionIn an arrangement shown , bob A on the left is pulled aside . It is then released and allowed to collide with other bob B which is at rest . A perfectly inelastic collision occurs and the system rises to a height h/4 . The ratio of the masses of the bobs is
View Solution