Deduce the expression for the torque experienced by a rectangular loop carrying a steady current ‘I’ and placed in a uniform magnetic field vector B. Indicate the direction of the torque acting on the loop.
Torque on a current carrying loop: Consider a rectangular loop PQRS of length l breadth b suspended in a uniform magnetic field vector B. The length of loop = PQ = RS= l and breadth = QR = SP = b. Let at any instant the normal to the plane of loop make an angle q with the direction of magnetic field vector B and I be the current in the loop. We know that a force acts on a current carrying wire placed in a magnetic field. Therefore each side of the loop will experience a force. The net force and torque acting on the loop will be determined by the forces acting on all sides of the loop. Suppose that the forces on sides PQ QR RS and SP are vector F1 vector F2 vector F3 and vector F4 respectively. The sides QR and SP make angle 90° - θ with the direction of magnetic field. Therefore each of the forces vector F2 and vector F4 acting on these sides has same magnitude F = Blbsin90° - θ = Blbcosθ. According to Fleming’s left hand rule the forces F2 and vector F4 are equal and opposite but their line of action is same. Therefore these forces cancel each other i.e. the resultant of vector F2 and vector F4 is zero. The sides PQ and RS of current loop are perpendicular to the magnetic field therefore the magnitude of each of forces vector F1 and vector F3 is F = IlBsin90° = IlB. According to Fleming’s left hand rule the forces vector F1 and vector F3 acting on sides PQ and RS are equal and opposite but their lines of action are different; therefore the resultant force of vector F1 and vector F3 is zero but they form a couple called the deflecting couple. When the normal to plane of loop makes an angle θ with the direction of magnetic field B the perpendicular distance between vector F1 and vector F3 is bsinθ. ∴ Moment of couple or Torque τ = Magnitude of one force F x perpendicular distance = BIl ×bsinθ = I lbBsinθ But lb = area of loop = A say ∴ Torque τ = IAB sinθ If the loop contains N-turns then τ = NI ABsinθIn vector form vector τ = NI vector A x vector B. Direction of torque is perpendicular to direction of area of loop as well as the direction of magnetic field i.e. along I vector A x vector B.
Related Solutions
A rectangular loop carrying a steady current is placed in a uniform magnetic field. Obtain the expression for the torque acting on the loop.
View SolutionDerive an expression for the torque on a rectangular coil of area A carrying. A current I and placed in a uniform magnetic field B. Indicate the direction the torque acting on the loop.
View SolutionA rectangular loop of area A and carrying a steady current I is placed in a uniform magnetic field:-Derive the expression of torque, tau = barmxxbarB acting on the loop.
View SolutionDeduce the expression for torque on a rectangular current loop in a uniform magnetic field.
View SolutionThe torque experienced by a rectangular current loop placed perpendicular to a uniform magnetic field is
View SolutionA rectangular loop carrying a current i is placed in a uniform magnetic field B. The area enclosed by the loop is A. If there are n turns in the loop, the torque acting on the loop is given by
View SolutionA rectangular loop carrying a current i is placed in a uniform magnetic field B. The area enclosed by the loop is A. If there are n turns in the loop, the torque acting on the loop is given by
View SolutionDerive an expression for torque acting on a rectangular current loop carrying coil placed in a uniform magnetic field.
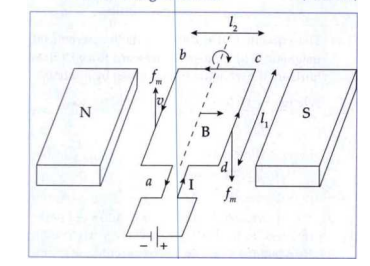
View SolutionDerive the expression for the torque acting on a current carrying loop placed in a magnetic field.
View SolutionDerive an expression for the torque acting on a rectangular current carrying loop suspended in a uniform magnetic field.
View SolutionA triangle loop of side l carries a steady current. It is placed in a magnetic field B such that normal of the place of loop is in the direction of B, the torque on the loop is ________
View SolutionThe torque experienced by a current loop in a magnetic field is vector form is given by i=_____.
View SolutionA rectangular current carrying loop PQRS is kept in a uniform magnetic field as shown in the figure. (a) What is the direction of magnetic moment of the current loop? (b) When is the torque acting on the loop (i) maximum, (ii) zero?
View SolutionDerive the expression for the torque acting on a current carrying loop placed in a magnetic field.
View SolutionWhat is the torque on a current carrying loop placed in a uniform magnetic field?
View SolutionCurrent Carrying Loop in Uniform Magnetic Field|Torque on a Loop
View SolutionWhat is the torque experienced by a current carrying loop kept in a magnetic field?
View Solutionएक आयताकार लूप जिसमें स्थायी धारा I प्रवाहित हो रही है, एकसमान चुंबकीय क्षेत्र B में स्थित है। लूप द्वारा अनुभव किए गए बल आघूर्ण के लिए व्यंजक व्युत्पन्न कीजिए। लूप पर लगने वाले बल आधूर्ण की दिशा बताइए।
View SolutionWrite the expression for the torque experienced by the loop in a magnetic field in vector form.
View SolutionThe torque acting on a rectangular loop having area A carrying current i and placed in a magnetic field Bî, with which the loop makes an angle o is given by
View Solution