Solve: d2y/dx2 = xex.
The given differential equation is d2y/dx2 = xexd/dydy/dx = xexIntegrating we get dy/dx = x – 1ex + c1Again integrating we get y = x – 2ex + c1x + c2which is the required solution.
Related Solutions
If then find the value of d2y/dx2 at θ=π/6
View SolutionIf , where C is constant of integration and then
View Solutionarlithmetic means are inserted between and then between If the rth means in each case be equal, then find the ratio
View Solutionarlithmetic means are inserted between and then between If the rth means in each case be equal, then find the ratio
View SolutionThe sides of a rhombus are parallel to . The diagonals of the rhombus intersect at (1, 2). If one vertex of the rhombus lies on the y-axis then possible values of the ordinates of this vertex are 1 (b) 2 (c) 3 (d) 4
View SolutionFor certain curve y = f (x) satisfying (d ^(2) y )/( dx ^(2)) = 6x - 4, a relative minimum value dx2 of 5, occurs at ct = 1. Find the global maximum value of function f, for x in [ 0, 2]
View SolutionThe probability of A solving a problem is 0.3 and the probability of B solving the problem is 0.6 . The probability that A solves the problem and B does not solve it is
View Solutionगणित का एक प्रश्न एक विधार्थी या तो हल कार सकता है या हल नहीं कार सकता है । उसके हल करने कि प्रायिकता और हल न करने कि प्रायिकता है । मानले कि विधार्थी के द्वारा हल नहीं किये जाने पर हल करने कि प्रायिकता है । विधार्थी के प्रश्न हल करने कि प्रायिकता ज्ञात कीजिए यदि है कि वह उस प्रश्न को हल कार चुका हो
View Solutionहल कीजिये :
हल कीजिये :
View Solutionதீர்க்க
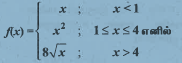
View Solutionsolve this
View Solutionsolve
View Solutionsolve
View Solution
View Solutionsolve
View Solution
View Solutionsolve this
View Solutionsolve
View Solutionsolve
View Solutionsolve
View Solution