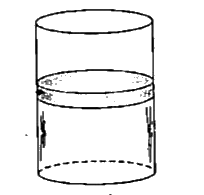
Figure 24-E2 shows a vessel partitioned by a fixed diathermic separator. Different ideal gases are filled in the two parts. The rms speed of the molecules in the left part equals the mean speed of the molecules in the right part. Calculate the ratio of the mass of a molecule in the left part to the mass of a molecule in the right part.
The left side of the container has a gas let having molecular wt. M1Right part has Mol. wt = M2Temperature of both left and right chambers are equal as the separating wall is diathermic
Related Solutions
Shows a vessel partitioned by a fixed diathermoc separator. Different ideal gases are filled in the two parts. The rms speed of the molecules in the left part is the mean speed of the molecules in the right part. Calculate the ratio of the mass of a molecule in the left part to the mass of a molecule in thej right part.

View SolutionShows a vessel partitioned by a fixed diathermoc separator. Different ideal gases are filled in the two parts. The rms speed of the molecules in the left part . The rms speed of the molecules in the right part. Calculate the ratio of the mass of a molecule in the left part to the mass of a molecule in thej right part.

View SolutionShows a vessel partitioned by a fixed diathermoc separator. Different ideal gases are filled in the two parts. The rms speed of the molecules in the left part . The rms speed of the molecules in the right part. Calculate the ratio of the mass of a molecule in the left part to the mass of a molecule in thej right part.

View SolutionA vessel is partitioned in two equal halves by a fixed diathermic separator. Two different ideal gases are filled in left (L) and right (R ) halves. The rms speed of the molecules in L part is equal to the mean speed of molecules in the R part. Then the ratio of the mass of a molecule in L part to that of a molecule in R part is

View SolutionA vessel is partitioned in two equal halves by a fixed diathermic separator. Two different ideal gases ae filled in left (L) and right (R) halves the rms speed of the molecules in L part is equal to the mean speed of moleucles in the R equal to the ratio of the mass of a molecules in L part to that of a molecules in R part is

View SolutionA vessel is partitioned in two equal halves by a fixed diathermic separator. Two different ideal gases ae filled in left (L) and right (R) halves the rms speed of the molecules in L part is equal to the mean speed of moleucles in the R equal to the ratio of the mass of a molecules in L part to that of a molecules in R part is

View SolutionA vessel is partitioned in two equal halves by a fixed diathermic separator. Two different ideal gases ae filled in left (L) and right (R) halves the rms speed of the molecules in L part is equal to the mean speed of moleucles in the R equal to the ratio of the mass of a molecules in L part to that of a molecules in R part is

View SolutionA vessel is partitioned in two equal halves by a fixed diathermic separator. Two different ideal gases are. filled in left and right halves. The rms speed of the molecules in part is equal to the mean speed of molecules in the part. If the ratio of the mass of a molecule in part to that of a molecule in part is . then find .
'(##CEN_KSR_PHY_JEE_C13_E01_011_Q03##)'
View SolutionA tube is divided into two time parts by a stationary bithermal separator. The left (L) and the right (R) part are filled with two different ideal gases. The msA of the gaseous molecules in the L-part is equal to the mean velocity of the molecules in the L-part Therefore, the ratio of the mass of the molecules present in the L part and the part will be-
View SolutionFigure-2.28 shows a cylindrical container which is divided in two equal parts by a clamped diathermic piston. Different ideal gases are filled in the two parts. It is found that the rms speed of molecules in the lower part is equal to the mean speed of molecules in the upper part. Find the ratio ofmass of molecule of gas in lower part to that of the gas in upper part.
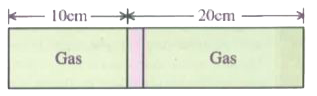
View SolutionFigure shows a horizontal cylindrical container of length 30 cm, which is partitioned by a tight fitting separator. The separator is diathermic but conducts heat very slowly. Initially the separator is in the state shown in figure. The temperature of left part of cylinder is 100K and that on right part is 400K. Initially the separator is in equilibrium. As heat is conducted from right to left part, separator displaces to the right. Find the displacement of separator after a long time when gases on the two parts of cylinder are in thermal equilibrium.
View Solutionदो समरूप पात्रों में समान तापमान पर दो भिन्न आदर्श गैसें हैं। यदि पहले पात्र में गैस अणुओं की औसत चाल दूसरे पात्र में अणुओं की सर्वाधिक प्रायिक चाल के बराबर है, तो पहले पात्र में गैस अणुओं के द्रव्यमान और दूसरे पात्र में गैस अणुओं के द्रव्यमान का अनुपात है
View SolutionDNA अणु का वह भाग जो विभिन्न DNA अणुओं में अलग - अलग होता है
View SolutionFig. shows a horzontal cylindrical container of length , which is partitioned by a tight-fiting separator. The separator is diathermic but conductws heat very slowly. Initially the separator is the state shown in the figure. The temperature of left part of cylinder is and that on right part is . Initially the separator is in equilibrium. As heat is conducted from right to left part, of separator after a long when gases on the two displacement of separator after a long when gases on the two parts of cylinder are in thermal equilibrium.

View SolutionFig. shows a horzontal cylindrical container of length 30 cm , which is partitioned by a tight-fiting separator. The separator is diathermic but conductws heat very slowly. Initially the separator is the state shown in the figure. The temperature of left part of cylinder is 100 K and that on right part is 400 K . Initially the separator is in equilibrium. As heat is conducted from right to left part, of separator after a long when gases on the two displacement of separator after a long when gases on the two parts of cylinder are in thermal equilibrium.
View SolutionFig. shows a horzontal cylindrical container of length , which is partitioned by a tight-fiting separator. The separator is diathermic but conductws heat very slowly. Initially the separator is the state shown in the figure. The temperature of left part of cylinder is and that on right part is . Initially the separator is in equilibrium. As heat is conducted from right to left part, of separator after a long when gases on the two displacement of separator after a long when gases on the two parts of cylinder are in thermal equilibrium.

View SolutionThe mass of molecule A is twice the mass of molecule B. The rms speed of A is twice the rms speed of B. If two samples of A and B contain same no. of molecules, what will be the ratio of P of two samples in separate containers of equal volume.
View SolutionThe mass of molecule A is twice the mass of molecule B. The rms speed of A is twice the rms speed of B. If two samples of A and B contain same number of molecules, what will be the ratio of pressures of two samples in separate containers of equal volume.________
View SolutionFigure shows a horizontal cylindical container of length 30cm, which is partitioned by a tight fitting separator. The separator is diathermic but conducts heat very slowly. Initially the separator is in the state shown in figure. The temperature of left part of cylinder is 100 K and that on right part is 400K Initially the separator is in equilibrium. As heat is conducted from right to left part, seprator displaces to the right. Find the displacment of separaJor after a long time, when gases on the parts of cylinder are in thermal equilibrium.
View SolutionA mixture of two ideal gases A and B is in thermal equilibrium at 600 K.A molecule of A has one-fourth the mass of a molecule of B and the rms speed of molecules of A is 400 m/s. Determine the rms speed of molecules of B.
View Solution