From a set of 11 square integers show that one can choose 6 numbers a2; b2; c2; d2; e2; f2 such that a2 + b2 + c2 ≡ d2 + e2 + f2 mod 12.
The first observation is that we can find 5 pairs of squares such that the two numbers in a pair have the same parity. We can see this as follows:Odd numbersEven numbersOdd pairsEven pairsTotal pairs0110551100552914538145472355623565325743258341592415101505110505Let us take such 5 pairs: say x21 ; y21; x22 ; y22; .... x25 ; y25. Then x2j - y2j is divisible by 4 for 1 ≤ j ≤ 5. Let rj be the remainder when x2j - y2j is divisible by 3 1 ≤ j ≤ 3. We have 5 remainders r1; r2; r3; r4; r5. But these can be 0 1 or 2. Hence either one of the remainders occur 3 times or each of the remainders occur once. If for example r1 = r2 = r3 then 3 divides r1 + r2 + r3; if r1 = 0; r2 = 1 and r3 = 2 then again 3 divides r1+r2+r3. Thus we can always find three remainders whose sum is divisible by 3. This means we can find 3 pairs say x21 ; y21; x22 ; y22; x23 ; y23 such that 3 divides x21 - y21 + x22 - y22+x23 - y23. Since each difference is divisible by 4 we conclude that we can find 6 numbers a2; b2; c2; d2; e2; f2 such that a2 + b2 + c2 ≡ d2 + e2 + f2 mod 12:
Related Solutions
Discussion OF Ex-9.4 (Optional)|| Important Result a2=b2+c2(PythagorasTheorem) ||Chapter summary
View SolutionIf the angles A,B,C of a triangle are in A.P.and sides a,b,c are in G.P. ,then a2,b2,c2 are in
View Solutionসংখ্যারেখা তৈরি করে নীচের সংখ্যাগুলিকে সংখ্যারেখায় দেখাও ও নাম দাও। +5, -2, +3, -6, +2, -5, -এ যথাক্রমে A,B,C,D,E ও F নাম দাও। B থেকে E-এর দূরত্ব কত ঘর মেপে দেখো।
View SolutionMolecular Orbital Diagram Of C2, N2 , O2 ,F2
View SolutionMolecular Orbital Diagram Of B2, C2 ,N2 |S-P Mixing
View SolutionIf the equation of the locus of a point equidistant from the points (a_1, b_1) and (a_2, b_2) is (a_1-a_2)x+(b_1-b_2)y+c=0 , then the value of c is a a2-a2 2+b1 2-b2 2 sqrt(a1 2+b1 2-a2 2-b2 2) 1/2(a1 2+a2 2+b1 2+b2 2) 1/2(a2 2+b2 2-a1 2-b1 2)
View SolutionIf the equation of the locus of a point equidistant from the points and is , then the value of is
View SolutionLet be a binary operation on the set Q of rational numbers as follows: find is it associative?
View SolutionLet be a binary operation on the set Q of rational numbers as follows: find is it commutative?
View SolutionThe ratios a1/a2 , b1/b2 , c1/c2 Find out whether the given linear equations are pairwise compatible or incompatible: 2x - 3y = 8 and 4x - 6y = 9.
View SolutionSuppose a set of rational numbers Q Defined below ** One of the two-dimensional processes is: a**b=a2-b2 Find out if this is a companion.
View SolutionSuppose a set of rational numbers Q Defined below ** One of the two-dimensional processes is: a**b=a2-b2 Find out if this is a rotation.
View SolutionA(a1, b1) மற்றும் B(a2, b2) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை X-அச்சு எந்த விகிதத்தில் பிரிக்கும்?
View SolutionIn the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
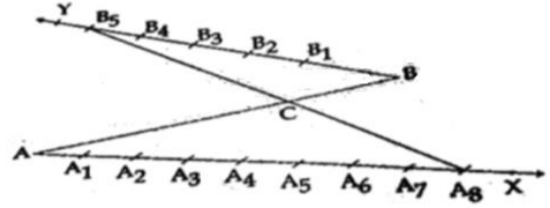 View Solution
View SolutionIf x = a cos θ and y = b sin θ, then b2x2 + a2y2 = …………… (1) a2b2 (2) ab (3) a4b4 (4) a2 + b2
View Solution35. If the sum of the roots of be equal to sum of the squares, then- (A) 2ac = ab + b2 (B) 2ab-bc + c2 c (D) None of these (D) None of these (C) 2bc -ac+2
View Solution0.जब C1 और C2 धरिता के संधारित समंतर क्रम में संयोगजीत किए जाते हैंपरिनामी धरिता है (A) C1+C2 (B) C1C2/(C1+C2) (C) (C1+C2)/C1C2 (D)C1/C2
View Solutionin A2-15=5A , A2 and 5A are two digit numbers, then find A.
View SolutionIn A2+1A = 45, A2 and 1A are two digit number, then find A
View SolutionE2 is
View Solution
