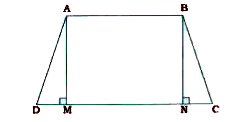
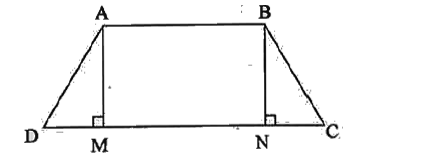
If the nonparallel side of a trapezium are equal prove that it is cyclic.
Given: ABCD is a trapezium whose two non-parallel sides AB and BC are equal. To Prove: Trapezium ABCD is a cyclic. Construction: Draw BE ║ AD. Proof : ∴ AB ║ DE [Given] AD ║ BE [By construction] ∴ Quadrilateral ABCD is a parallelogram. ∴ ∠BAD = ∠BED ....i [Opp. angles of a║gm] And AD = BE ....ii [Opp. sides of a ║gm] But AD = BC ...iii [Given] From ii and iii BE = BC ∴ ∠BEC = ∠BCE ....iv [Angles opposite to equal sides] ∠BEC + ∠BED = 1800 [Linear Pair Axiom] ⇒ ∠BCE + ∠BAD = 1800 [From iv and i] ⇒ Trapezium ABCD is cyclic. [∴ If a pair of opposite angles of a quadrilateral 180 0 then the quadrilateral is cyclic]
Related Solutions
If the non parallel sides of a trapezium are equal. Prove that it is cyclic.
View SolutionIf the non parallel sides of a trapezium are equal, Prove that it is cyclic.
 View Solution
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
View Solutionयदि एक समलंब की असमान्तर भुजाएँ बराबर हो, तो सिद्ध कीजिए कि वह चक्रीय है ।
View Solutionसिद्ध कीजिए कि चक्रीय समांतर चतुर्भुज आयत होता है।
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
 View Solution
View Solutionयदि एक समलम्ब की असमान्तर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है |
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
 View Solution
View SolutionProve that the slant sides of a cyclic trapezium are equal.
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
View SolutionIf the non-parallel sides of a trapezium are equal, prove that it is cyclic.
View Solutionकिसी चक्रीय समलम्ब चतुर्भुज की सम्मुख भुजाएँ बराबर है, तो सिध्द कीजिए कि उनके विकर्ण भी बराबर होंगे।
View SolutionThe parallel sides of a trapezium are 25cm and 13cm; its nonparallel sides are equal, each being 10cm, find the area of the trapezium.
View SolutionThe parallel sides of a trapezium are 25cm and 13cm; its nonparallel sides are equal, each being 10cm, find the area of the trapezium.
View SolutionIf two non-parallel sides of a trapezium are equal, then prove that it is cyclic
View SolutionIf two sides of a cyclic quadrilateral are parallel, prove that the remaining two sides are equal and the diagonals are also equal. OR A cyclic trapezium is isosceles and its diagonals are equal.
View SolutionIf two sides of a cyclic quadrilateral are parallel, prove that the remaining two sides are equal and the diagonals are also equal. OR A cyclic trapezium is isosceles and its diagonals are equal.
View SolutionIf two non-parallel sides of a trapezium are equal; it is cyclic.
View SolutionIf two non-parallel sides of a trapezium are equal; it is cyclic.
View Solution11.The parallel sides of a trapezium are 20cml and 10cm. Its nonparallel sides are both equal.each being 13cm. Find the area of the trapezium.
View Solution
