Show that the diagonals of a parallelogram divide it into four triangles of equal area.
We know that diagonals of parallelogram bisect each other. Therefore O is the mid-point of AC and BD.BO is the median in ΔABC. Therefore it will divide it into two triangles of equal areas.∴ Area ΔAOB = Area ΔBOC ... 1In ΔBCD CO is the median.∴ Area ΔBOC = Area ΔCOD ... 2Similarly Area ΔCOD = Area ΔAOD ... 3From equations 1 2 and 3 we obtainArea ΔAOB = Area ΔBOC = Area ΔCOD = Area ΔAODTherefore it is evident that the diagonals of a parallelogram divide it into four triangles of equal area.
Related Solutions
दर्शाइए कि समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाटते है।
View Solutionदर्शाइए कि समांतर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलो वाले चार त्रिभुजों के बाँटते है ।
View Solutionदिखाएँ की किसी समांतर चतुर्भुज के विकर्ण उसे समान क्षेत्रफल वाले चार त्रिभुजों में विभाजित करते है|
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
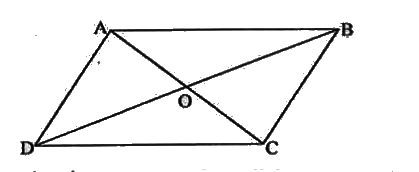
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
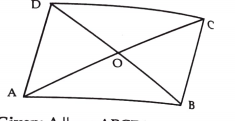
View SolutionA diagonal of parallelogram divides it into four triangles of equal area.
View SolutionA diagonal of parallelogram divides it into four triangles of equal area.
View Solutionसिद्ध कीजिए कि समान्तर चतुर्भुज के विकर्ण उस समान्तर चतुर्भुज को बराबर क्षेत्रफल के चार त्रिभुजों में बाँटते है।
View SolutionProve that two diagonals of a parallelogram divides it into four triangles of equal areas.
View Solutionಸಮಾಂತರ ಚತುರ್ಭುಜದ ಕರ್ಣಗಳು ಅದನ್ನು ಸಮಾನ ವಿಸ್ತೀರ್ಣದ ನಾಲ್ಕು ತ್ರಿಭುಜಗಳಾಗಿ ವಿಂಗಡಿಸುತ್ತವೆ ಎಂದು ಸಾಧಿಸಿ.
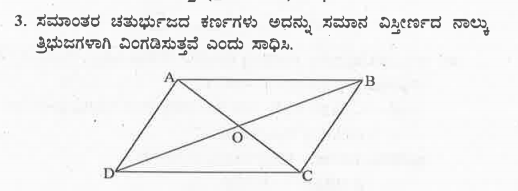
View Solution