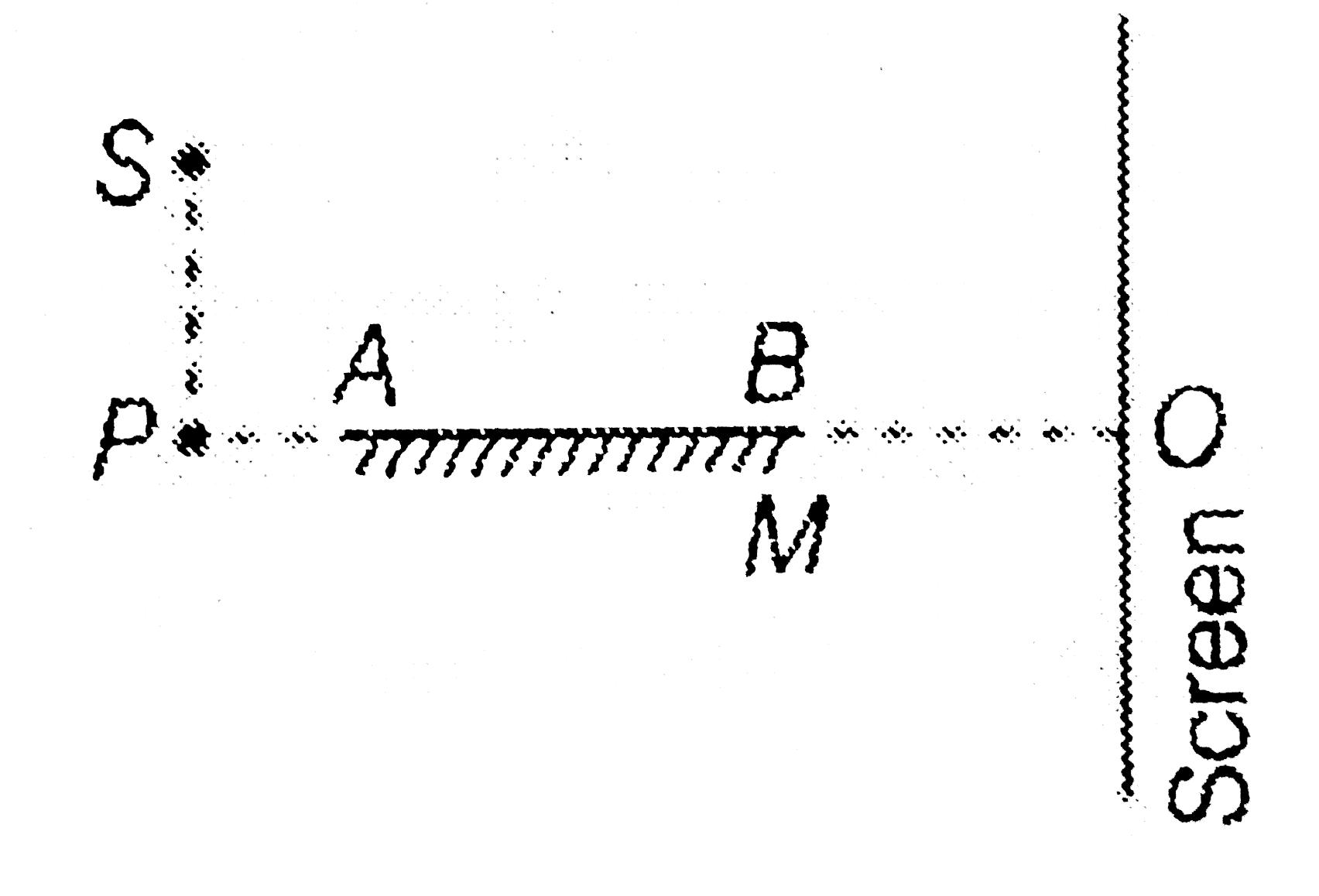
Figure 5.14 illustrates the interference experiment with Fresnel mirrors. The angle between the mirrors is α = 12 the distances from the mirrors intersection line to the narrow slit S and the screen Sc are equal to r = 10.0 cm and b = 130 cm respectively. The wavelength of light is λ = 0.55 μm. Find: a the width of a fringe on the screen and the number of possible maxima;b the shift of the interference pattern on the screen when the slit is displaced by δl = 1.0 mm along the arc of radius r with centre at the point O; c at what maximum width δmax of the slit the interference fringes on the screen are still observed sufficiently sharp.
2 b α is the length of the spot on the screen which gets light after reflection from both mirror. We add 1 above to take account of the fact that in a distance Δx there are two maxima.b When the silt moves by δl along the arc of radius r the incident ray on the mirror rotates by δl/r; this is the also the rotation of the reflected ray. There is then a shift of the fringe of magnitude.c If the width of the slit is δ then we can imagine the slit to consist of two narrow slits with separation δ. The fringe pattern due to the wide slit is the superposition of the pattern due to these two narrow slits are 1/2 Δx apart because then the maxima due to one will fill the minima due to the other. Thus we demand that
Related Solutions
Figure. Illustrates the interference axperiment with Fresnel mirrors. The angle between the mirrors is alpha = 12' the distance from the mirrors intersection line to the narrow slit S and the screen Sc are equal to r= 10.0 cm and b = 130 cm resoectively. the wavelength of light is lambda = 0.55 mu m . Find: (a) the width of a fringe on the screen and the number of possible maxima, (b) the shift of the interference pattern on the screen when the slit is displaced by del l = 1.0 mm along the are of radius r with centre at the point O , (c) at what maximum width del_(max) of the slit the interference fringes on the screen are still observed sufficiently sharp.
View SolutionIn Lloyd's mirror experiment (Fig.) a light wave emitted directly be the source (narrow slit) interferes with the wave reflected form a mirror . As s result, an interference fringe pattern is

formed on the screen . the source and the mirror are separated by a distance .At a certain position of the source the fringe width on the screen was equal to , and after source was moved away from the mirror plane by , the fringe width decreased times. Find the wavelength of light.
View SolutionThe distances from a Fresnel prisum to a narrow slit and a screen are equal to a = 25 cm and b = 100 cm respectively. The refracting angles of the glass biprism is equal to theta = 20 . Find the wavelength of light if the width of the fringe on the screen is Delta x = 0.55 mm .
View SolutionA Lloyd's mirror or length 5 cm is illuminated with monochromatic light of wavelength lambda (= 6000 Å) from a narrow 1 mm slit in its plane and 5 cm plane from its near edge. Find the fringe width on a screen 120 cm from the slit and width of interference pattern on the screen.
View SolutionA Lloyd's mirror or length 5 cm is illuminated with mon ochromatic light of wavelength lambda (= 6000 Å) from a narrow 1 mm slit in its plane and 5 cm plane from its near edge. Find the fringe width on a screen 120 cm from the slit and width of interference pattern on the screen.
View SolutionIn Lloyd's single mirror interference experiment, the source slit is at a distance of 2 mm from the plane mirror . The screen is kept at a distance of 1.5m from the source . If light of wavelength 5890 is used, calculate the fringe width.
View SolutionA plane light wave falls on Fresnel mirrors at an inclination of alpha = 2 . Detrmine the wavelength of light if the width of fringe on the screen is beta = 0.55 m :
View SolutionIn a Lloyds's mirror experiment as narrow slit S transmitting a light of wavelength is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?
View SolutionIn a double experiment, the distance between the slit is 1 mm and screen is 25 cm away from the slits. The wavelength of light is . The width of the fringe on the screen is
View SolutionA slit illuminated by monochromatic light is held 0.4 mm from the surface of a plane mirror. The fringe width in the interference pattern obtained with reflected and direct light is 0.25 mm. The screen is at 50 cm from the slit. The wavelength of light is
View SolutionIn a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.

If the mirror is shifted towards left then how does the fringe pattern on screen changes ?
View SolutionA plane light wave falls on Fresnel mirrors with an angle alpha = 2.0 between them. Determine the wavelength of light if the width of the fringe on the screen Delta x = 0.55 mm .
View SolutionTwo plane mirrors, a source S of light, emitting wavelengths of lambda_(1) = 4000overset(@)A" and" lambda_(2) = 5600overset(@)A and a screen are arranged as shown in figure. The angle theta shown is 0.05 radian and distance a and b are 1 cm and 38 cm respectively. (a) Find the fringe width of interference pattern formed on screen by the blue light. (b) Calculate the distance of first black line from central bright fringe. (c) Find the distance between two black lines which are nearest to the central bright fringe.
View SolutionIn a Young’s double slit experiment, the slit separation is , the distance between the screen and slit is 1 m . Wavelength of the light used is . The distance between two consecutive dark fringes (in mm ) is
View SolutionThe distance between the two slits in Young's double slit experiment is 0.02 cm. Interference fringes for light of wavelength 6000 Å are formed on the screen at a distance of 80 cm from the slits. Determine the distance of the fifth bright fringe.
View SolutionIn a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength lambda is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P. If fringe width is 0.1 mm then what is the wavelength of light used ?
View SolutionIn a double slit interference experiment, the distance between the slits is 0.05 cm and screen is 2m away from the slits. The wavelength of light is 8.0xx10^(-5) cm. The distance between successive fringes is
View SolutionMonochromatic light from a narrow slit illuminates two narrow slit 0.3 mm apart producing an interference pattern with bright fringes 1.5 mm apart on a screen 75 cm away. Find the wavelength of the light. How will the fringe width altered if the distance of the screen is doubled .
View SolutionA long narrow horizontal slit lies 1 mm above a plane mirror. The interference pattern produced by the slit and its and its image is viewed on a screen sum distance 1m from the slit. The wavelength of light is 600 nm . Then the distance of the first maxima above the mirror is equal to (d lt lt D) :
View SolutionA long narrow horizontal slit lies above a plane mirror. The interference pattern produced by the slit and its and its image is viewed on a screen distance from the slit. The wavelength of light is . Then the distance of the first maxima above the mirror is equal to :

View Solution