A mixture of equal masses of water and icem = mw = mice = 1 kg is contained in a thermally insulated cylindrical vessel under a light piston. The pressure on the piston is slowly increased from the initial value p0 =105 Pa to p1 = 2.5 x 106 Pa. The specific heats of water and ice are cw = 4.2 kJ/kg . K and cice = 2.1 kJ/kg . K the latent heat of fusion of ice is λ = 340 kJ/kg and the density of ice is ρice = 0.9ρw where ρw is the density of water.Determine the mass Δm of ice which melts in the process and the work A done by an external force if it is known that the pressure required to decrease the fusion temperature of ice by 1°C is p = 14 x 106 Pa while the pressure required to reduce the volume of a certain mass of water by 1% is p = 20 x 106 Pa.1 Solve the problem assuming that water and ice are incompressible.2 Estimate the correction for the compressibility assuming that the compressibility of ice is equal to half that value for water.
1 Assuming that water and ice are incompressible we can find the decrease in the temperature of the mixture as a result of the increase in the external pressure:Such a small change in temperature indicates that only a small mass of ice will melt i.e. Δm << mice.We write the energy conservation law:Let us estimate the work A done by the external force. The change in the volume of the mixture as a result of melting ice of mass Δm isWe have taken into account the fact that the density of water decreases as a result of freezing by about 10% i.e. Therefore we obtain an estimateThe amount of heat ΔQ required fot heating the mass m of ice and the same mass of water by ΔT isSince A << ΔQ . we can assume that λ Δm = ΔQ whenceThe change in volume as a result of melting ice of this mass isConsidering that for a slow increase in pressure the change in the volume ΔV is proportional to that in the pressure Δp we can find the work clone by the external force:2 We now take into account the compressibility of water and ice. The change in the volume of water and ice will bewhere V0w =10-3 m3 and V0ice = 1.1 x 10-3 m3 are the initial volumes of water and ice. The work A done by the external force to compress the mixture isThe total work of the external force isObviously since we again have Atot << ΔQ the mass of the ice that has melted will be the same as in case 1.
Related Solutions
2 kg of ice at is mixed with 5 kg of water at in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container. Given specific heat capacities of water and ice are respectively. Latent heat of fusion of ice (in kg)
View Solution4 kg of ice at is mixed with 10 kg of water at in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container, Given : Specific heat capacities of water and ice are respectively. Molar enthalpy of fusion of ice is
View Solution4 kg of ice at is mixed with 10 kg of water at in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container, Given : Specific heat capacities of water and ice are respectively. Molar enthalpy of fusion of ice is
View SolutionA vessel of negligible heat capacity contains 5-0 kg of water at C. If 5.0 kg of ice at C is added to it, find : (i) heat energy imparted by water in fall of its temperature from C to C, (ii) mass of ice melted, (iii) final temperature of mixture, and (iv) mass of water at C in mixture. Given : specific heat capacity of water = 4200 J , specific latent heat of ice = 336 kJ .
View Solution273 K पर 1 kg बर्फ को 383 K के जल भाप में बदलने पर एन्ट्रॉपी में परिवर्तन होगा। (जल तथा भाप की विशिष्ट ऊष्मा क्रमश: 4.2 kJ एवं 2491 kJ हैं, संग्लन की ऊष्मा तथा पानी की वाष्पीकरण ऊष्मा क्रमश: 334 kJ एवं 2491 kJ है) (log 273=2.436 , log 373 = 2.572 , log383=2.583 )
View Solution273 K पर 1 kg बर्फ को 383 K के जल भाप में बदलने पर एन्ट्रॉपी में परिवर्तन होगा। (जल तथा भाप की विशिष्ट ऊष्मा क्रमश: 4.2 kJ एवं 2491 kJ हैं, संग्लन की ऊष्मा तथा पानी की वाष्पीकरण ऊष्मा क्रमश: 334 kJ एवं 2491 kJ है) (log 273=2.436 , log 373 = 2.572 , log383=2.583 )
View Solution1 Kg of ice at is mixed with 2 Kg of water at . Assuming that there is no loss of energy to the environment, what will be the final temperature of the mixture ? (Assume latent heat of ice = KJ/Kg, specific heat of water and ice are and , respectively.)
View SolutionThe specific heat of Argon at constant volume is 0.3122kJ/kg K. Find the specific heat of Argon at constant pressure if R = 8.314 kJ/k mole K. (Molecular weight of argon = 39.95) in kJ/kg K is.
View SolutionA 0.60 kg sample of water ans a sample of ice are placed in two compartments A and B that are separated by a conducting wall in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperatures T of the liquid water and the ice are given in graph as functions of time t. Temperatures of the compartments remain homogeneous during the whole heat transfer process.
Given, specific heat of ice = 2100 J/kg-K
Specific heat of water = 4200 J/kg-K
latent heat of fusion of ice = J/kg
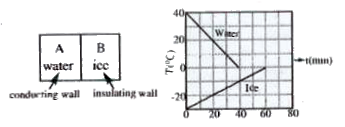
The initial mass of the ice in the container is equal to
View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . Initial mass of the ice in the container equal to
View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . Initial mass of the ice in the container equal to
View SolutionA 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100 J//kg-K , specific heat of water =4200 J//kg-K , and latent heat of fusion of ice =3.3xx10^5 J//kg . Initial mass of the ice in the container equal to
View SolutionAir is contained in a vertical piston – cylinder assembly fitted with an electric heater. The piston has a mass of 50 kg and cross sectional area of . Mass of the air inside the cylinder is 0.3 kg. The heater is switched on and the volume of the air slowly increases by . It was found that the internal energy of the air increased by and that of the piston increased by 0.06 kJ/kg. Assume that the container walls and outer surface of the piston are well insulated and there is no friction. The atmospheric pressure is 100 kPa. Determine the heat transferred by the heater to the system consisting of air and the piston.
View SolutionA beaker contains 0.1 kg of water, initially at room temperature . If the specific heat of water is 4.2 kJ/kg and the latent heat of vaporization is 2,300kJ/kg, how much thermal energy would the water need to absorb to turn completely to steam?
View SolutionFind the heat energy required to convert 10 g ice at 0^(@)C to steam at 100^(@)C . Specific latent heat of melting and vapourization are 336 KJ kg^(-1) and 2260 KJ kg^(-1) , respectively, and specific heat of water is 4200 J kg^(-1)K^(-1).
View Solution2kg of ice at -20^@C is mixed with 5kg of water at 20^@C in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container. It is given that the specific heats of water & ice are 1kcal//kg//^@C and 0.5 kcal//kg//^@C while the latent heat of fusion of ice is 80kcal//kg
View Solution2kg of ice at 20^@C is mixed with 5kg of water at 20^@C in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container. It is given that the specific heats of water & ice are 1kcal//kg//^@C and 0.5 kcal//kg//^@C while the latent heat of fusion of ice is 80kcal//kg
View Solution2kg of ice at is mixed with 5kg of water at in an insulating vessel having a negligible heat capacity. Calculate the final mass of water remaining in the container. It is given that the specific heats of water & ice are
while the latent heat of fusion of ice is
View SolutionWhen 5 kg of water is heated 20^(@) If raised from C to its boiling point, then the heat absorbed by it will be (specific heat of water = 4.2 "kJ "kg^(-1) c^(-1) )
View SolutionThe amount of heat energy required to convert 1 kg of ice at -10^@ C to water at 100^@ C is 7,77,000 J. Calculate the specific latent heat of ice. Specific heat capacity of ice = 2100 J kg^(-1) K^(-1) , specific heat capacity of water = 4200 J kg^(-1) K^(-1) .
View Solution