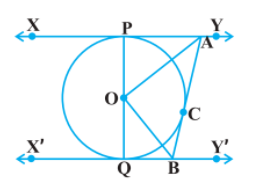
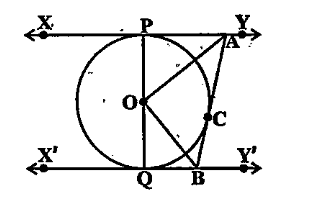
In given figure XY and XY are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and XY at B. Prove that ∠AOB = 900.
Join OCIn ΔOPA and ΔOCAOP = OC radii of same circlePA = CAlength of two tangents from an external point
Related Solutions
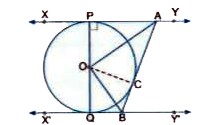
In the given figure 4.13 ,xy and x'y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting xy at A and x'y' at B. Prove that .
View SolutionIn Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that
View SolutionIn the given figure. XY and X are two parallel tangent to a circle with centre O and another tangent AB with point of contact C is intersecting XY at A and X at B. Prove that
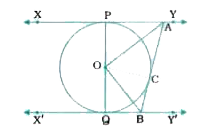
View SolutionIn the given figure ,XY and XY are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X'Y' ar B.Prove that

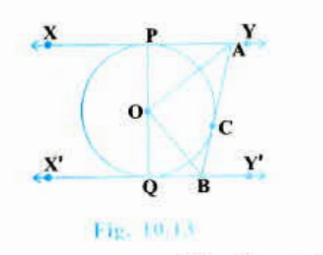
View SolutionIn Fig, 10.13, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AR with point of contact C intersecting XY at A and X'Y' at B. Prove that .
View SolutionIn the figure XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of cantact C intersecting XY at A and X'Y' at B then angle AOB=

View Solutionदी गई आकृति में XY तथा X 'Y ', O केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिंदु C पर स्पर्श रेखा AB, XY को A तथा X 'Y ' को B पर प्रतिच्छेद करती है । सिद्ध कीजिए कि है ।
View SolutionXY and X'Y' are two parallel tangents to the circle with centre at O. Antoher tangent AB touches the circle at C and XY at A and X'Y' at B. Prove that .
View Solutionदिये चित्र में, XY तथा X'Y' ,O केन्द्र वाले किसी वृत्त पर दो समान्तर स्पर्श रेखाएँ है और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को Y तथा X' Y' को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि .

View Solutionआकृति में XY तथा X'Y', O केन्द्र वाले किसी वृत्त पर दो समान्तर स्पर्श रेखाएँ है और स्पर्श बिन्दु C पर स्पर्श रेखा AB , XY को A तथा X'Y' को B पर प्रतिच्छेद करती है। सिद्ध कीजिए कि है।

View SolutionIn Fig, 10.13, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AR with point of contact C intersecting XY at A and X'Y' at B. Prove that .

View SolutionIn Fig.10.13, XYandX'Y' are two parallel tangent to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X'Y' at B.Prove that.
View SolutionChoose the correct answer and give justification for each.
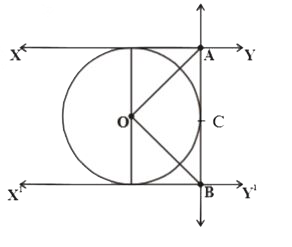
In the figure XY and are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and at B then
View SolutionChoose the correct answer and give justification for each.
In the figure XY and are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and at B then

View Solutionਚਿੱਤਰ 10.13 ਵਿੱਚ XY ਅਤੇ X'Y', O ਕੇਂਦਰ ਵਾਲੇ ਕਿਸੇ ਚੱਕਰ 'ਤੇ ਦੋ ਸਮਾਂਤਰ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ਅਤੇ ਸਪਰਸ਼ ਬਿੰਦੂ C 'ਤੇ ਸਪਰਸ਼ ਰੇਖਾ AB,XY ਨੂੰ A ਅਤੇ X'Y' ਨੂੰ 'Bਤੇ ਕੱਟਦੀ ਹੈ।ਸਿੱਧ ਕਰੋ ਹੈ।

View SolutionIn the figure, XY and X'Y 'are parallel tangents to a circle with an' O 'circle center, and another tangent AB pulled at the touch point A intersects XY at point A and X' Y 'at point B. If so angleAOB = 90^@ Prove that.
View Solutionare tangents to a circle, is another tangent to the circle at the point R on the circle, which intersects at respectively. If , then is
View SolutionXY and XZ are tangents to a circle. ST at the point R of the circle is another tangent intersecting XY and XZ at S and T respectively. If XY = 15 cm. and TX=9 cm. If so, what is the length of RT?
View SolutionIn the given figure, AB is a diameter of the circle with centre O and XY is the tangent at a point C. If , then what is the value (in degrees) of ?

View SolutionIn the given figure, AB is a diameter of the circle with centre O and XY is the tangent at a point C. If , then what is the value (in degrees) of ?
View Solution