In Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that ∠AOB=90∘
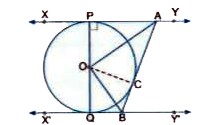
Step by step video & image solution for In Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that angle AOB = 90^@ by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLES BOOK - VK GLOBAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - PROFICIENCY EXERCISE (Long Answer Questions 4 mark)
12 Videos
- ARITHMETIC PROGRESSIONS BOOK - VK GLOBAL PUBLICATIONCHAPTER - ARITHMETIC PROGRESSIONS EXERCISE - SELF ASSESSMENT TEST
10 Videos
- COORDINATE GEOMETRY BOOK - VK GLOBAL PUBLICATIONCHAPTER - COORDINATE GEOMETRY EXERCISE - SELF-ASSESSMENT TEST
10 Videos
Similar Questions
XYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
View Solutionlandm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
View Solution
Knowledge Check
PQ and RS are two parallel tangents to a circle with centre O and another tangent AB wih point of contact C intersect PQ at A and RS at B. then find ∠AOB
A60∘B120∘C90∘D180∘XYandXZare tangents to a circle, STis another tangent to the circle at the point R on the circle, which intersects XYandXZat SandT respectively. If XY=15cmandTX=9cm, then RTis
A4.5 cmB7.5 cmC6 cmD3 cmIf lhe tangent to the curve x+y=exy be parallel to y-axis, then the point of contact is
A(1, 0)B(0,1)C(1,1)DNone
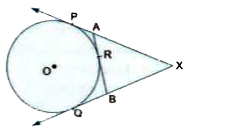
In Fig , XP and XQ are two tangents to the circle with centre O , drawn from an external point X . ARB is another tangent, touching the circle at R . Prove that XA + AR = XB + BR.
View SolutionIn Fig common tangents AB and CD to two circles with centres O1andO2 intersect at E. Prove that AB = CD.
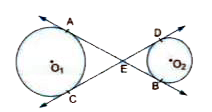
View SolutionThe common tangents AB and CD to two circles with centres O and O' intersect at E between the centres. Prove that the points O, E and O' are collinear.
View SolutionIf Fig , AOB is diameter of a circle with centre O and AC is a tangent to the circle at A . If ∠BOC=130∘ , then find ∠ACO .

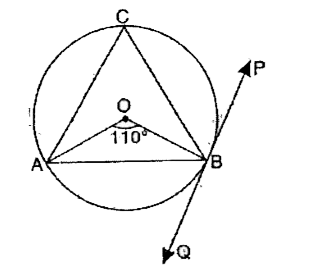
View SolutionIn the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
View Solution
