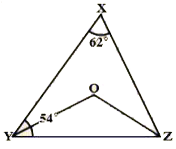
In the figure ∠ X = 62° ∠ XYZ = 54°. If YO and ZO are the bisectors of ∠ XYZ and ∠ XZY respectively of ∆ XYZ find ∠OZY and ∠YOZ.
In the given figure ∠X = 62° and ∠XYZ = 54°∠XYZ + ∠XZY + ∠YXZ = 180° …i [Angle sum property of a triangle] ⇒ 54° + ∠XZY + 62° = 180° ⇒ ∠XZY + 116° = 180° ⇒ ∠XZY = 180° – 116° = 64° Now ∠OZY = 1/ 2 × ∠XZY [∵ZO is bisector of ∠XZY] = 1 /2 × 64° = 32° Similarly ∠OYZ = 1/2 × 54° = 27° Now in ∆OYZ we have ∠OYZ + ∠OZY + ∠YOZ = 180° Angle sum property of a triangle] ⇒ 27° + 32° + ∠YOZ = 180° ⇒ ∠YOZ = 180° – 59° = 121° Hence ∠OZY = 32° and ∠YOZ = 121° Ans.
Related Solutions
In the given fig.
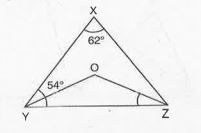 , . If YO and ZO are the bisectors of and respectively of , find and .
, . If YO and ZO are the bisectors of and respectively of , find and .
View Solutionआकृति में, और है । यदि YO और ZO क्रमश: के और के समद्विभाजक है, तो और ज्ञात कीजिये ।
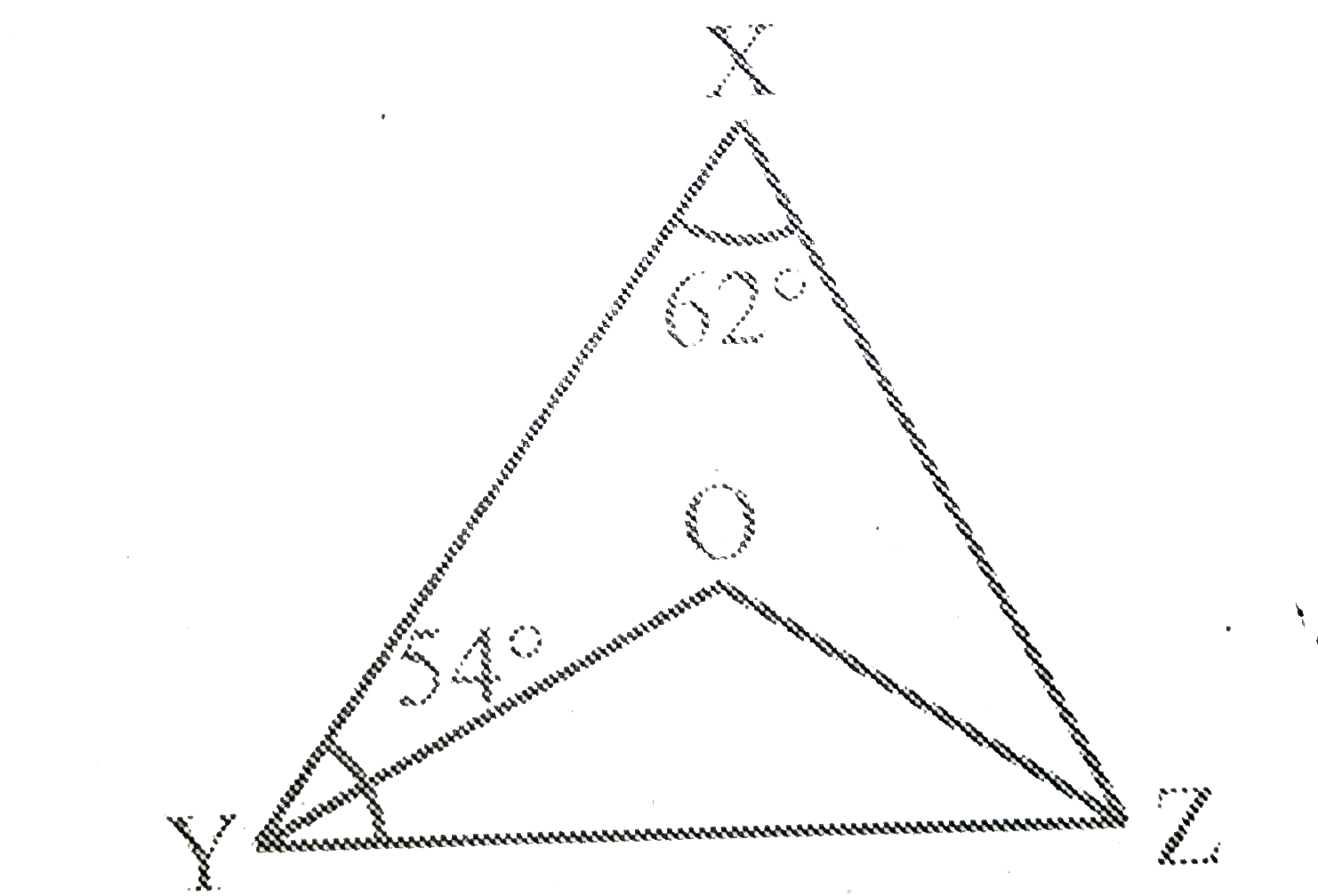
View Solutionआकृति में, और है । यदि YO और ZO क्रमश: के और के समद्विभाजक है, तो और ज्ञात कीजिये ।

View SolutionIn figure, . If YO and ZO are bisectors of respectively of is
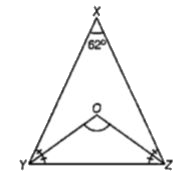
View SolutionIn figure, . If YO and ZO are bisectors of respectively of is

View Solutionਚਿੱਤਰ 6.40 ਵਿਚ, ਅਤੇ ਹੈ। ਜੇਕਰ YO ਅਤੇ ZO ਕ੍ਰਮਵਾਰ ਦੇ ਅਤੇ ਦੇ ਸਮਦੁਭਾਜਕ ਹੋਣ, ਤਾਂ ਅਤੇ ਪਤਾ ਕਰੋ।

View Solutionఇచ్చిన పటంలో ∠X=62°, ∠XYZ = 54° ∆XYZ లో∠XYZ మరియు∠XZY' ల కోన సమద్విఖండన రేఖలు వరుసగా YO మరియు ZO అయిన ∠OZY మరియు∠YOZ ల కొలతలు కనుగొనండి.
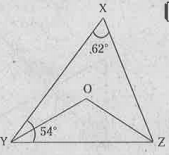
View SolutionIn figure, , If YO and ZO are the bisectors of respectively of , find .
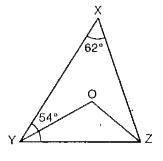
View SolutionIn Fig. 6.40, . If YO and ZO are the bisectors of and respectively of find and .

View SolutionIn the picture angleX = 62^@ , angleXYZ = 54^@ triangleXYZ At YO and ZO respectively angleXYZ And angleXZY If the angles are, OZY And angleYOZ Find out.
View SolutionFrom the figure find x and y.
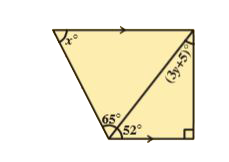
View SolutionIn the given figure, . In If YO and ZO are the bisectors of and respectively find and
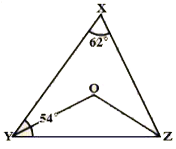
View SolutionIn the Figure If YO and ZO are the bisectors of respectively of .
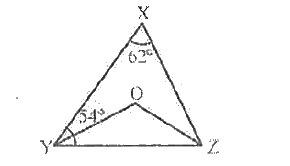
View SolutionIn the given figure, . If YO and ZO are the bisectors of and respectively of , find and angleYOZ.

View SolutionIn the given figure, . In If YO and ZO are the bisectors of and respectively find and
View SolutionIn the given figure, . In If YO and ZO are the bisectors of and respectively find and

View Solutionआकृति में , और है । यदि YO और ZO क्रमश : के और के समद्विभाजक है , तो और ज्ञात कीजिए ।
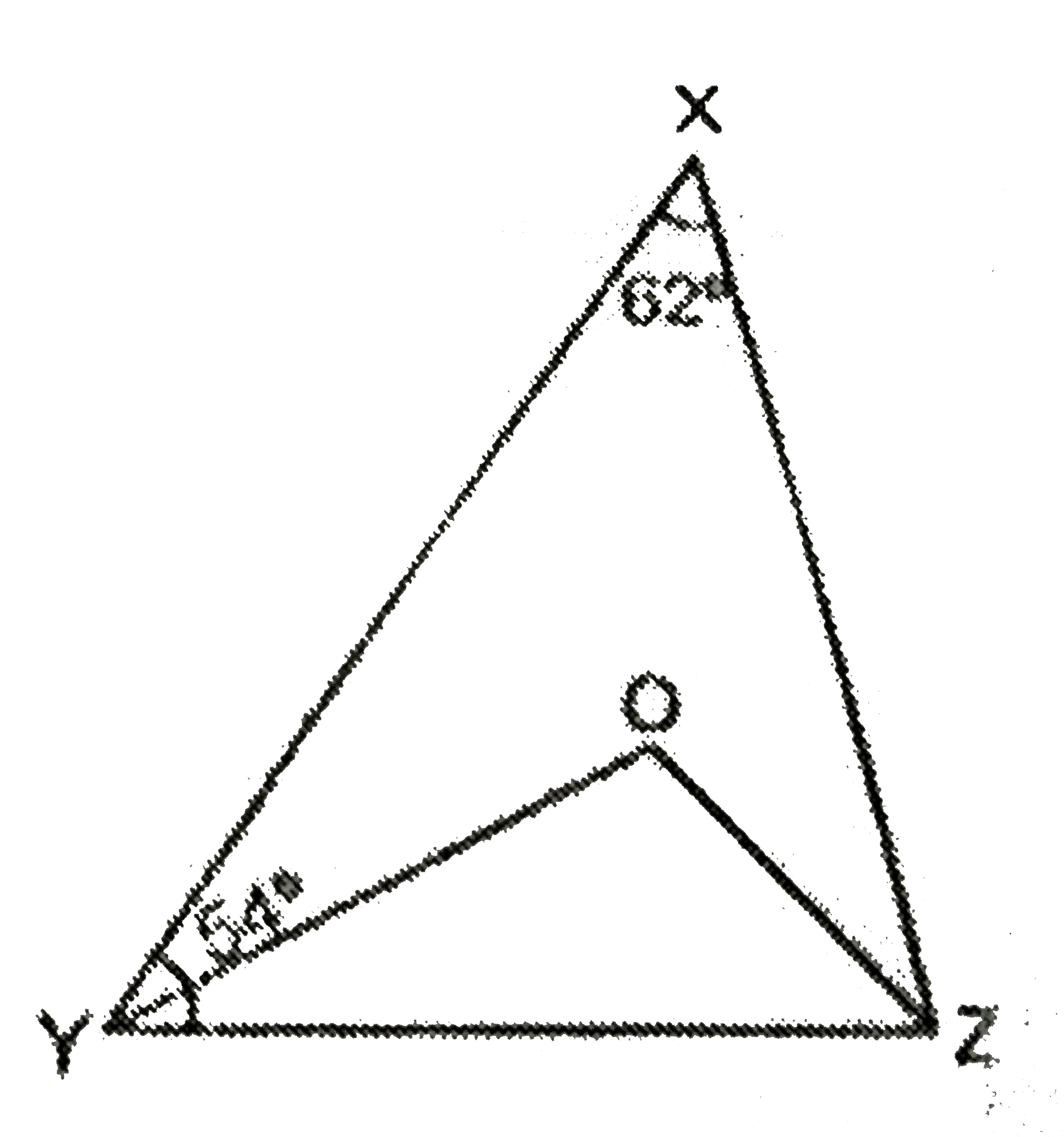
View SolutionIn the given fig.
 , . If YO and ZO are the bisectors of and respectively of , find and .
, . If YO and ZO are the bisectors of and respectively of , find and .
View SolutionIn the given fig.
 , . If YO and ZO are the bisectors of and respectively of , find and .
, . If YO and ZO are the bisectors of and respectively of , find and .
View SolutionIn the given fig.
 , . If YO and ZO are the bisectors of and respectively of , find and .
, . If YO and ZO are the bisectors of and respectively of , find and .
View Solution