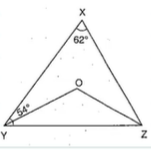
In Fig. 6.40, ∠X=62∘,∠XYZ=54∘. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.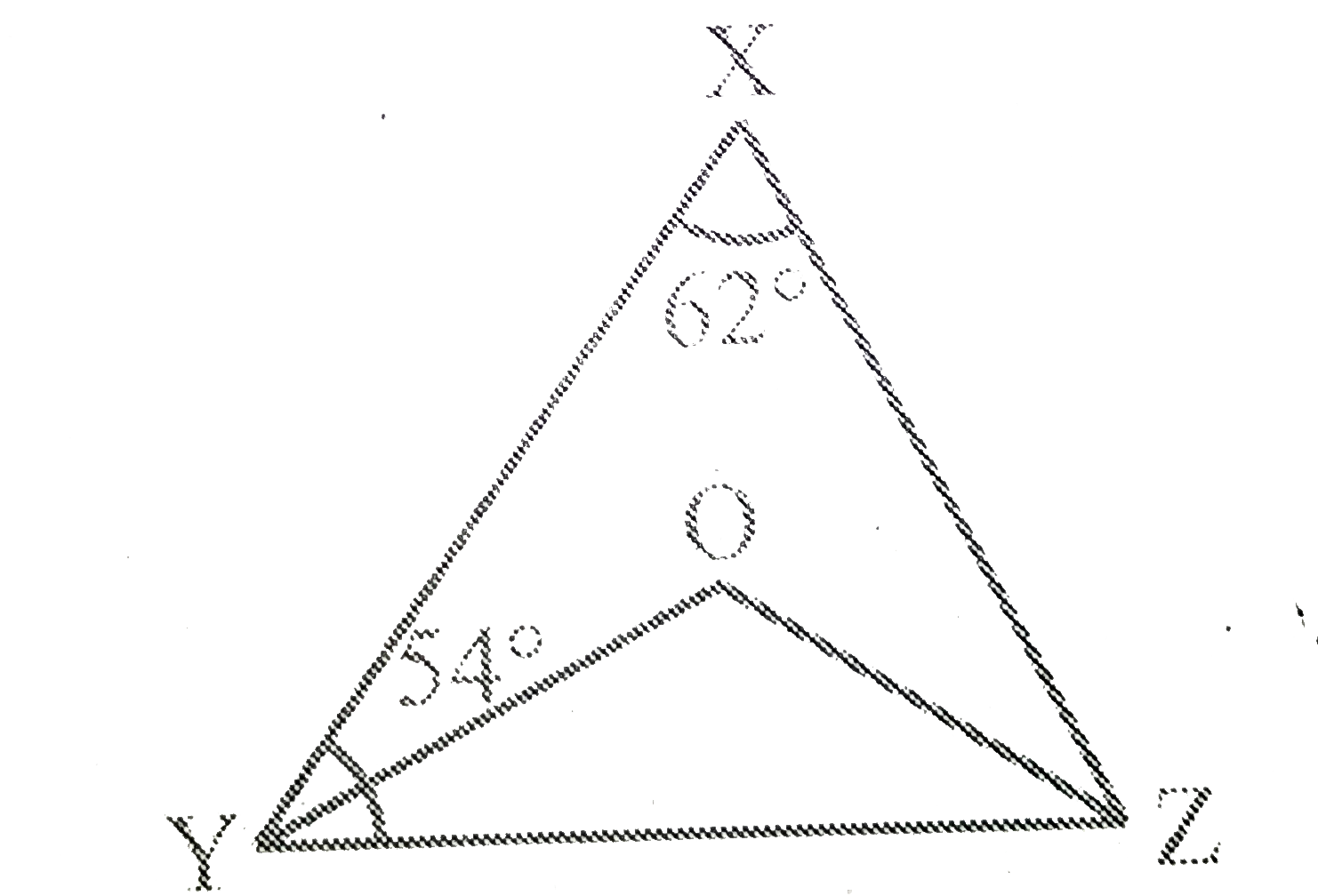
Video Solution
Text Solution
As the sum of all interior angles of a triangle is 180º, therefore, for ΔXYZ,
∠X + ∠XYZ + ∠XZY = 180º
62º+54º+ ∠XZY = 180º
∠XZY = 180º−116º
∠XZY =64º
∠OZY = 32º (OZ is the angle bisector of ∠XZY)
Similarly, ∠OYZ == 27º
Using angle sum property for ΔOYZ, we obtain
∠OYZ + ∠YOZ + ∠OZY = 180º
27º + ∠YOZ +32º = 180º
∠YOZ =180º−59º
∠YOZ = 121º
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If ⎡⎢⎣x−y−z−y+zz⎤⎥⎦=⎡⎢⎣053⎤⎥⎦ then the values of x,y and z are respectively
A5,2,2B1,−2,3C0,−3,3D11,8,3 - Question 2 - Select One
If x, y, z are real numbers such that x+y+z=4 and x2+y2+z2=6, then x,y,z lie in :
A[3/2,2]B[2/3,2]C[0,2/3]Dnone of these - Question 3 - Select One
If x=yz,y=zx and z=xy, then
Axyz=1Bxyz=1Cx+y+z=1Dxz = y
If (xy)z = xy^z where each of x, y and z is greater than 1, then find y in terms of z.
View SolutionIf x(x+y+z)=4,y(x+y+z)=16andz(x+y+z)=29 and x, y & z are positive numbers. Find x, y & z=?
View SolutionIf x,zandy are in A.P. where x,y and z are distinct numbers then evaluate xx−z+zy−z
View Solutionx+y+z=6
x−y+z=2
2x+y−z=1
then x,y,z are respectivelyView SolutionIf x(x+y+z)=20,y(x+y+z)=30andz(x+y+z)=50 the vaue of 2 (x + y + z) is
View Solution