Prove that the straight lines joining the mid points of the sides of a quadrilateral ABCD taken in order form a parallelogram.
Let the position vectors of A B C and D be vectora b c and vector d. Hence position vectors of P Q R and S the mid points of AB BC CD & DA respectively areVector PQ is parallel and equal to Vector SR. Hence PQRS is a parallelogram.
Related Solutions
Using vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View SolutionUsing vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View Solutionसिद्ध कीजिए कि किसी चतुर्भुज कि क्रमागत भुजाओं के मध्य-बिंदुओं को मिलाने से बना चतुर्भुज समान्तर चतुर्भुज होता है।
View SolutionSide of a equilateral triangle is 7 ,find its hight.
View SolutionProve that the quadrilatral formed by joining the mid points of the sides of a quadrilateral is a parallelogram.
View SolutionIf the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).

View SolutionIf the mid-point of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram so formed will be half of the area of the given quadrilateral.
View SolutionIf the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).

View SolutionThe figure formed by joining the mid-points of the sides of a quadrilateral taken in order is
View SolutionThe figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only, if
View SolutionThe figure formed by joining the mid-points of the sides of a quadrilateral ABCD taken in order is a square only, if
View SolutionThe figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only, if
View SolutionProve that the lines joining the midpoints of consecutive sides of a quadrilateral form a parallelogram using vector method.
View SolutionThe quadrilateral formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a rectangle, if
View SolutionThe quadrilateral formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a rhombus, if
View SolutionIf the mid-points of the sides of a quadrilateral are joined in sequence, then prove that the area of the parallelogram so formed is half of the area of the given quadrilateral.
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
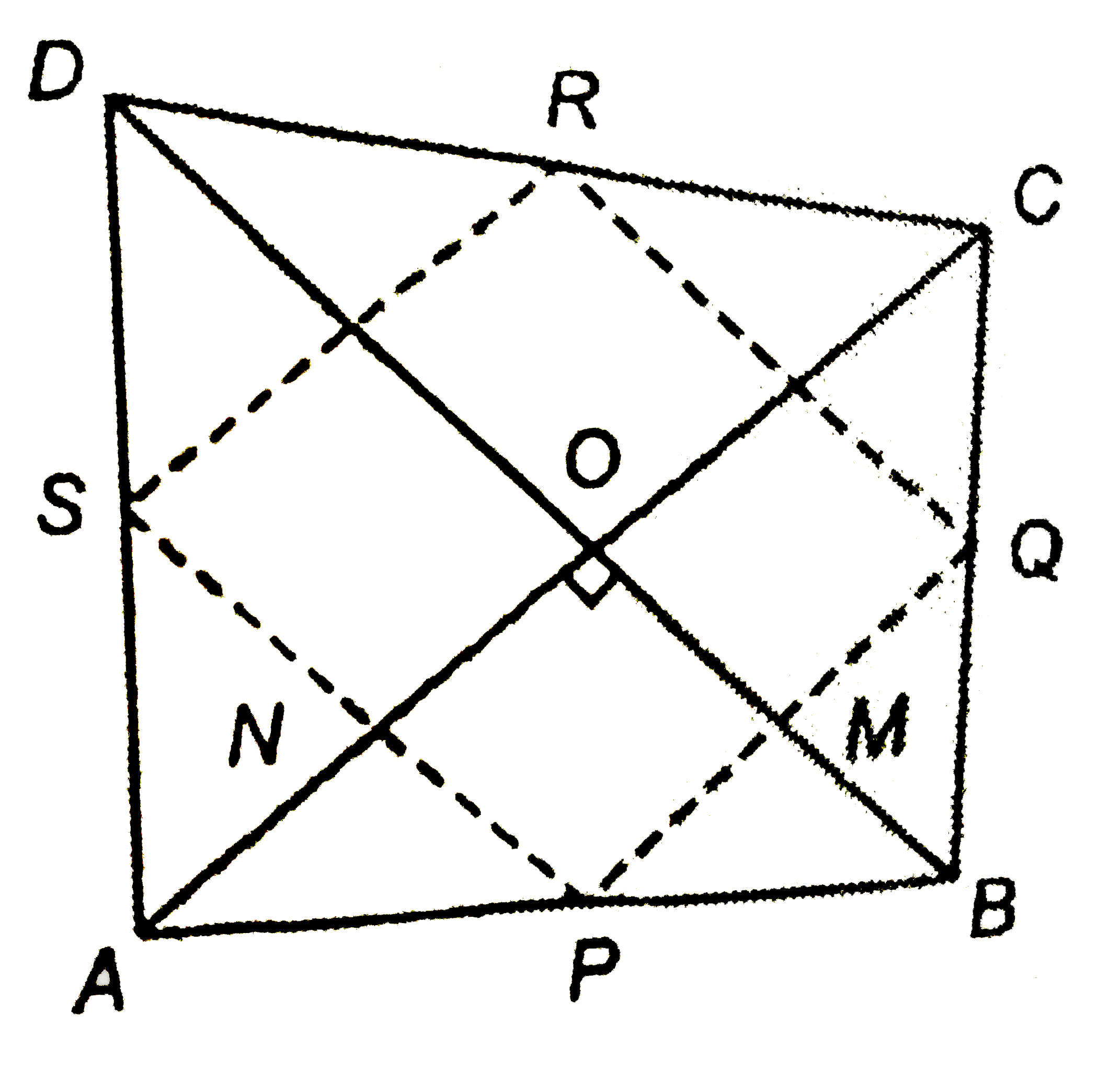
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.

View Solution