Question

Prove that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.

Explanation

To prove that the quadrilateral formed by joining the midpoints of the pairs of consecutive sides of a quadrilateral is a parallelogram, we will follow these steps:

Step 1: Define the Quadrilateral and Midpoints
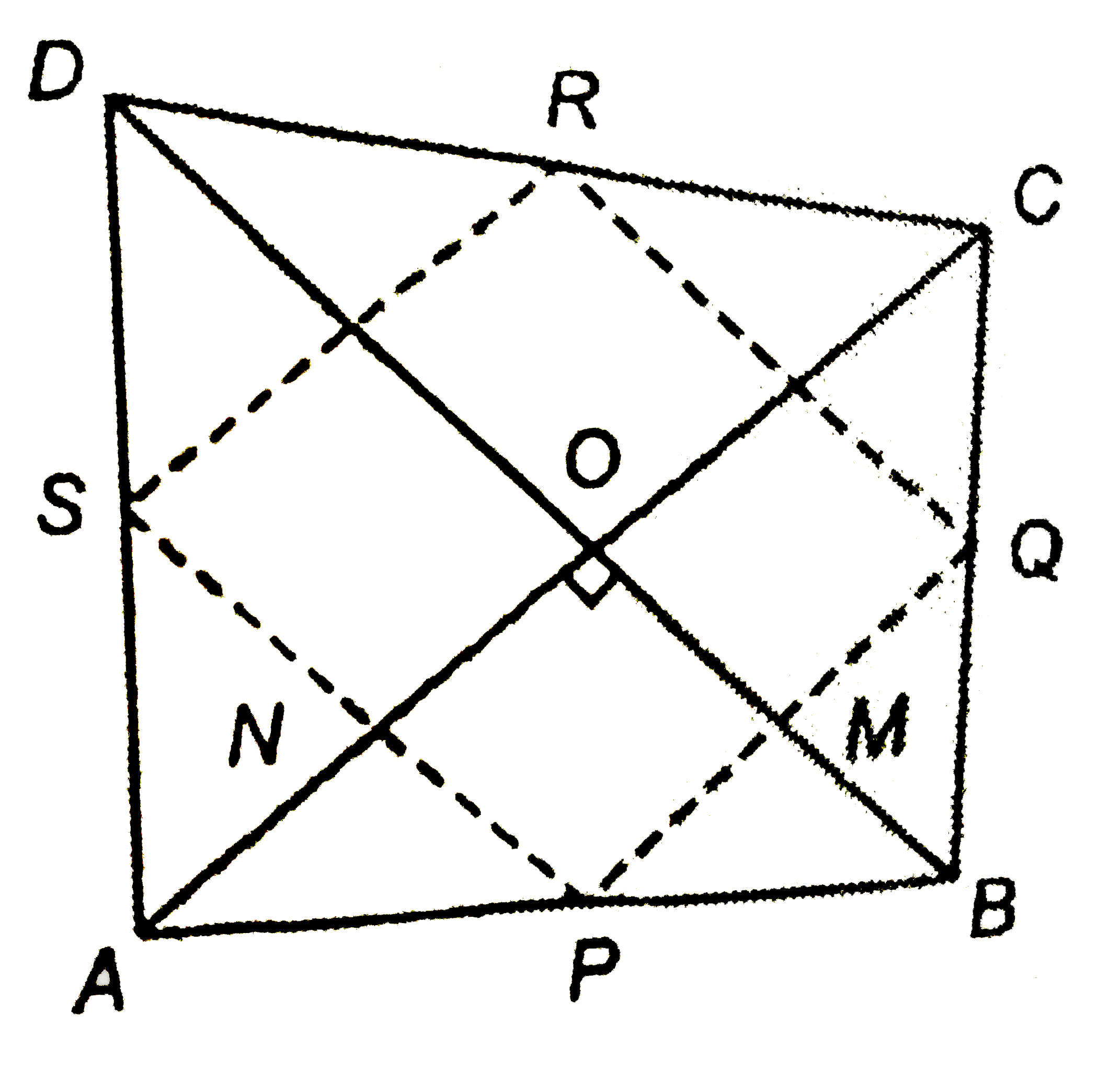
Let \( A \), \( B \), \( C \), and \( D \) be the vertices of the quadrilateral. The midpoints of the sides \( AB \), \( BC \), \( CD \), and \( DA \) are denoted as \( P \), \( Q \), \( R \), and \( S \) respectively.

Step 2: Express the Midpoints in Vector Form
Using position vectors, we can express the midpoints as follows:
- \( P = \frac{\vec{A} + \vec{B}}{2} \) (midpoint of \( AB \))
- \( Q = \frac{\vec{B} + \vec{C}}{2} \) (midpoint of \( BC \))
- \( R = \frac{\vec{C} + \vec{D}}{2} \) (midpoint of \( CD \))
- \( S = \frac{\vec{D} + \vec{A}}{2} \) (midpoint of \( DA \))

Step 3: Find the Vectors \( \vec{PQ} \) and \( \vec{SR} \)
Next, we need to find the vectors \( \vec{PQ} \) and \( \vec{SR} \):
- The vector \( \vec{PQ} \) is given by:
\( \vec{PQ} = \vec{Q} - \vec{P} = \left( \frac{\vec{B} + \vec{C}}{2} \right) - \left( \frac{\vec{A} + \vec{B}}{2} \right) = \frac{\vec{C} - \vec{A}}{2} \)

- The vector \( \vec{SR} \) is given by:
\( \vec{SR} = \vec{R} - \vec{S} = \left( \frac{\vec{C} + \vec{D}}{2} \right) - \left( \frac{\vec{D} + \vec{A}}{2} \right) = \frac{\vec{C} - \vec{A}}{2} \)

Step 4: Show that \( \vec{PQ} \) is Parallel to \( \vec{SR} \)
From the calculations above, we can see that:
\( \vec{PQ} = \vec{SR} \)
This means that \( \vec{PQ} \) is parallel to \( \vec{SR} \).

Step 5: Show that \( \vec{QR} \) is Parallel to \( \vec{SP} \)
Now, we will find the vectors \( \vec{QR} \) and \( \vec{SP} \):
- The vector \( \vec{QR} \) is given by:
\( \vec{QR} = \vec{R} - \vec{Q} = \left( \frac{\vec{C} + \vec{D}}{2} \right) - \left( \frac{\vec{B} + \vec{C}}{2} \right) = \frac{\vec{D} - \vec{B}}{2} \)

- The vector \( \vec{SP} \) is given by:
\( \vec{SP} = \vec{P} - \vec{S} = \left( \frac{\vec{A} + \vec{B}}{2} \right) - \left( \frac{\vec{D} + \vec{A}}{2} \right) = \frac{\vec{B} - \vec{D}}{2} \)

Step 6: Conclude that \( \vec{QR} \) is Parallel to \( \vec{SP} \)
Since \( \vec{QR} = -\vec{SP} \), we can conclude that \( \vec{QR} \) is also parallel to \( \vec{SP} \).

Final Conclusion
Since we have shown that both pairs of opposite sides \( \vec{PQ} \parallel \vec{SR} \) and \( \vec{QR} \parallel \vec{SP} \), we can conclude that the quadrilateral \( PQRS \) is a parallelogram.