सिद्ध करे कि
cot−19+cosec−1√414=π4
cot−19=tan−119 ...(1)
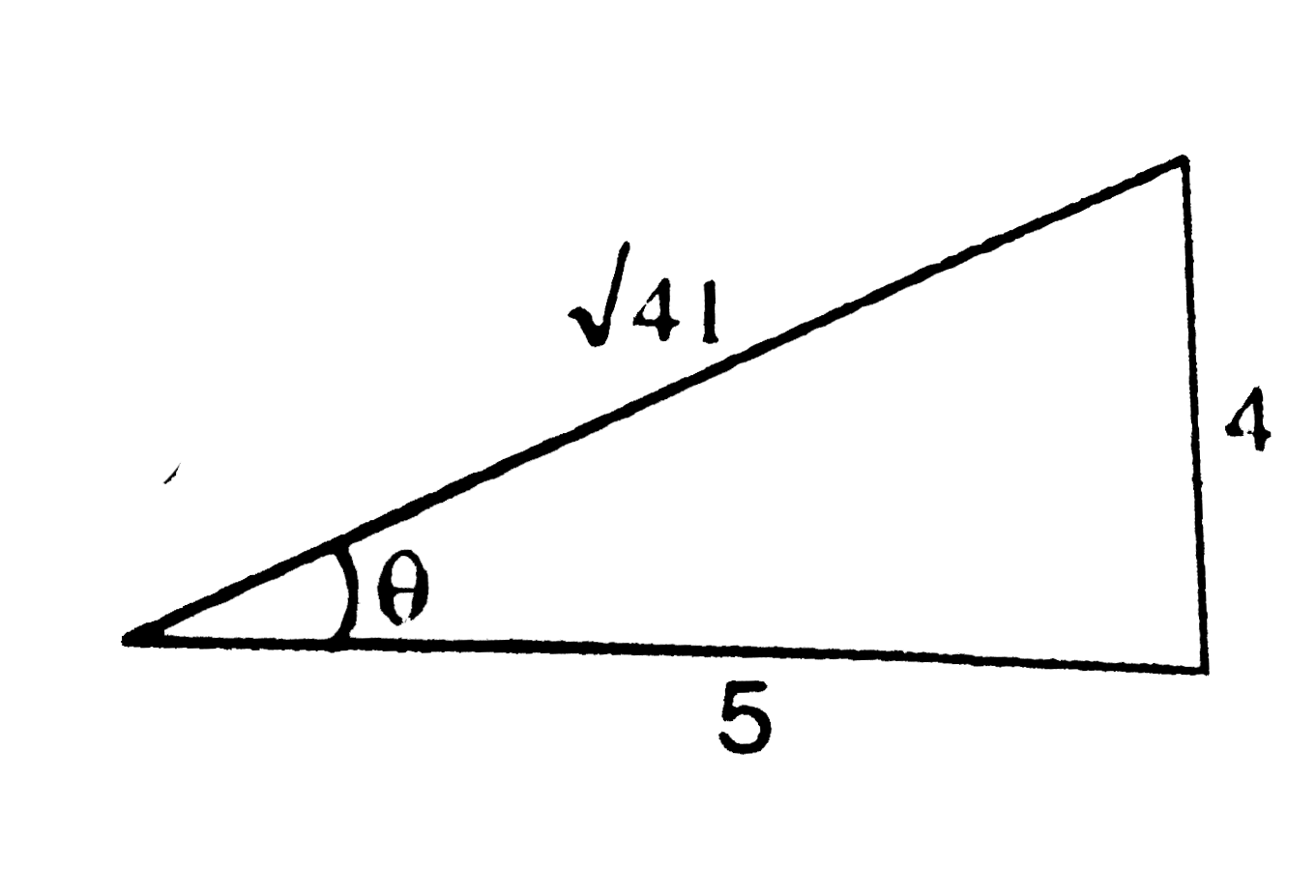
माना कि cosec−1√414=θ ∴cosecθ=√414
चूँकि हमे केवल मुख्य शाखा मान पर विचार करना है,
∴−π2≤θ≤π2 तथा θ≠0
चूँकि यहाँ cosecθ धन है, इसलिए θ,0 और π2 के बीच में है | अतः tanθ धन होगा |
अब, tanθ=45
⇒θ=tan−145
अर्थात cosec−1√414=tan−145 ...(2)
(1) और (2) को जोड़ने पर,
L.H.S.=tan−119+tan−145
=tan−1⎡⎣19+451−19×45⎤⎦=tan−1(4141)
=tan−1(1)=π4=R.H.S.
Topper's Solved these Questions
- प्रतिलोम त्रिकोणमितीय फलन BOOK - KC SINHACHAPTER - प्रतिलोम त्रिकोणमितीय फलन EXERCISE - अभ्यास 4.1
76 Videos
- निश्चित समाकलों के गुणधर्म BOOK - KC SINHACHAPTER - निश्चित समाकलों के गुणधर्म EXERCISE - OBJECTIVE QUESTIONS
39 Videos
- प्रायिकता का गुणन प्रमेय BOOK - KC SINHACHAPTER - प्रायिकता का गुणन प्रमेय EXERCISE - 32.2
24 Videos
Similar Questions
मान निकालें :
sin−1(√32)
View Solution∫π0cos2m+1 x dx, where m is a positive integar is equal to
View Solutionएक न्यायय सिक्का और एक अभिनत पाए को उछाला गया । मान ले A घटना 'सिक्के पर चित प्रकट होता है और B घटना 'पास पर संख्या 3 प्रकट होती है' को निरूपित करते है। परीक्षण कीजिए की घटनाएँ A और B स्वतंत्र है या नहीं ?
View Solution4(cot^(-1)3+csc^(-1)sqrt(5))=pi
View SolutionProve that cot−19+cosec−1√414=π4
View Solutioncot^(-1)9+cosec^(-1)(sqrt(41))/(4)=(pi)/(4)
View SolutionEvaluate the following expression: cosec(sec−1√414)
View Solutionसिद्ध कीजिए कि cot−19+cosec−1√414=π4
View Solutionसिद्ध करे कि
4(cot−13+cosec−1√5)=π.
View Solutionसिद्ध कीजिए की :
cot−13+cosec−1√5=π4
View Solution4(cot−13+cosec−1√5)=π
View SolutionProve that Cot−19+Cosec−1√414=π4.
View Solutioncot−19+cosec−1(√414)=
View Solutioncot−19+cosec−1(√414)=π4 అని రుజువు చేయండి.
View Solutionprove the following
cot−19+cosec−1√414=π4
View Solutioncot−19+cosec−1√414=
View Solution
