एक यादृच्छिक चर X का निम्नलिखित प्रायिकता बंटन है :
X01234567P(X)0k2k2k3kk22k27k2+k
ज्ञात करें (i) k (ii) P(X>6) (iii) P(0<X<3)
(i) 7ΣX=0P(X)=1
⇒0+k+2k+2k+3k+k2+2k2+(7k2+k)=1
⇒10k2+9k−1=0⇒(k+1)(10k−1)=0
⇒k=110 [∵k>0]
(ii) P(X>6)=P(X=7)=7k2+k=7100+110=17100
(iii) P(0<x<3)=P(X=1)+P(X=2)
=k+2k=3k=310
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - यादृच्छिक चर और प्रायिकता बंटन EXERCISE - अभ्यास 34.1 Type I.7videos
यादृच्छिक चर और प्रायिकता बंटन
- BOOK - KC SINHACHAPTER - यादृच्छिक चर और प्रायिकता बंटन EXERCISE - अभ्यास 34.1 Type II.16videos
यादृच्छिक चर और प्रायिकता बंटन
- BOOK - KC SINHACHAPTER - बरनौली परीक्षण और द्विपद बंटन EXERCISE - OBJECTIVE QUESTIONS10videos
बरनौली परीक्षण और द्विपद बंटन
- BOOK - KC SINHACHAPTER - रैखिक प्रोग्रामनEXERCISE - OBJECTIVE QUESTIONS5videos
रैखिक प्रोग्रामन
Similar Questions
X012P(X)0.20.60.2
04:48View Solutionदो सिक्को के एक साथ उछाल में यादृच्छिक चर पटो की संख्या X का प्रायिकता बंटन ज्ञात कीजिए।
03:53View SolutionIn a box containing 100 bulbs , 10 are defective. What is the probability that out of a sample of 5 bulbs, none is defective ?
03:08View SolutionThe corner pont sof the feasible region determined by the followign system of linear inequalities :2x+y≤10,x+3y≤15,xy≥0 are (0,0),(5,0),(3,4) and (0,5). Let Z=px+qy where p,q≥0. Conditions on p and q so that the maximum of Z occurs at both (3,4) and (0,5) is
08:04View SolutionA random variable X has the following probability distribution: I 0 1 2 3 4 5 6 7 P (X) 0 K 2K 2K 3K K2 2K2 7K2+K Determine: (i) K (ii) P(X<3) (iii) P(X > 6) (iv) P (0 < X < 3)
03:56View SolutionA random, variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 P(X):0 k 2k 2k 3k k2 2k2 7k2+k Find each of the following: i. k ii. P(X<6) iii. P(X≥6) iv. P(0<X<5)
03:42View Solutionएक यादृच्छिक चर X का प्रायिकता फलन P(X) निम्न प्रकार से है, जहाँ k कोई संख्या है।
P(X)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩k यदि (if) X = 02k यदि (if) X = 13k यदि (if) X = 20 अन्यथा
(i) k का मान ज्ञात कीजिए
(ii) P(X<2),P(X<2),P(X≥2) ज्ञात कीजिए।06:31View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया गया हैं-
X01234567P(X)0k2k2k3kk22k27k2+k
ज्ञात कीजिये-
(i) k, (ii) P(X≥3)
(iii) P(X≤6) , (iv) P(0<x<3)01:35View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन निचे दिया गया है-
∣∣∣X:01234567P(X):0k2k2k3kk22k27k2+k∣∣∣
ज्ञात कीजिए-
P(X<6)03:52View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन निचे दिया गया है-
∣∣∣X:01234567P(X):0k2k2k3kk22k27k2+k∣∣∣
ज्ञात कीजिए-
P(X≥6)04:15View Solutionएक यादृच्छिक चर X का प्रायिकता बंटन निचे दिया गया है-
∣∣∣X:01234567P(X):0k2k2k3kk22k27k2+k∣∣∣
ज्ञात कीजिए-
P(0<X<5).07:03View SolutionProbability distribution of x is
x01234p(X1)0.1k2k2kk
Find k .01:38View SolutionThe probability distribution of a random variable is given below:
X=x01234567P(X=x)0k2k2k3kk22k27k2+k
Then P(0<X<5)=06:03View SolutionA random variable X has the probability distribution given below. Its variance is
X12345P(X=x)k2k3k2kk07:30View Solutionएक याद्द्च्छिक चर X का प्रायिकता बंटन नीचे दिया गया है-
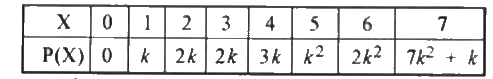ज्ञात कीजिये-
(i) k
(ii) P(X < 6)
(iii) P(X ge 6) (iv) P(0 < X <5)03:15View Solution