A random variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 , P (X): 0 K 2K 2K 3K K2 2K2 7K2+K Determine: (i) K (ii) P(X<3) (iii) P(X > 6) (iv) P (0 < X < 3)
To solve the problem step by step, we will follow the instructions given in the video transcript.
Step 1: Set up the probability distribution
We are given the random variable X with the following values and corresponding probabilities:
XP(X)001K22K32K43K5K262K277K2+K
Step 2: Write the equation for the sum of probabilities
Since the sum of all probabilities must equal 1, we can write the equation:
0+K+2K+2K+3K+K2+2K2+(7K2+K)=1
Step 3: Simplify the equation
Combining like terms, we get:
(0+K+2K+2K+3K+K+7K2+2K2)=1
This simplifies to:
(9K+10K2)=1
Step 4: Rearrange the equation
Rearranging gives us:
10K2+9K−1=0
Step 5: Solve the quadratic equation
We can use the quadratic formula K=−b±√b2−4ac2a where a=10,b=9,c=−1:
K=−9±√92−4⋅10⋅(−1)2⋅10
Calculating the discriminant:
92−4⋅10⋅(−1)=81+40=121
Now substituting back into the quadratic formula:
K=−9±√12120=−9±1120
Calculating the two possible values for K:
1. K=220=110
2. K=−2020=−1 (not valid since probabilities cannot be negative)
Thus, we have:
K=110
Step 6: Calculate P(X<3)
Now we need to find P(X<3):
P(X<3)=P(X=0)+P(X=1)+P(X=2)=0+K+2K=0+110+2⋅110=0+110+210=310
Step 7: Calculate P(X>6)
Next, we calculate P(X>6):
P(X>6)=P(X=7)=7K2+K
Substituting K=110:
P(X=7)=7(110)2+110=7⋅1100+110=7100+10100=17100
Step 8: Calculate P(0<X<3)
Finally, we find P(0<X<3):
P(0<X<3)=P(X=1)+P(X=2)=K+2K=110+2⋅110=310
Summary of Results
(i) K=110
(ii) P(X<3)=310
(iii) P(X>6)=17100
(iv) P(0<X<3)=310
We are given the random variable X with the following values and corresponding probabilities:
Since the sum of all probabilities must equal 1, we can write the equation:
Combining like terms, we get:
Rearranging gives us:
We can use the quadratic formula K=−b±√b2−4ac2a where a=10,b=9,c=−1:
2. K=−2020=−1 (not valid since probabilities cannot be negative)
Now we need to find P(X<3):
Next, we calculate P(X>6):
Finally, we find P(0<X<3):
(i) K=110
(ii) P(X<3)=310
(iii) P(X>6)=17100
(iv) P(0<X<3)=310
Topper's Solved these Questions
Similar Questions
A random variable X has the following probability distribution:
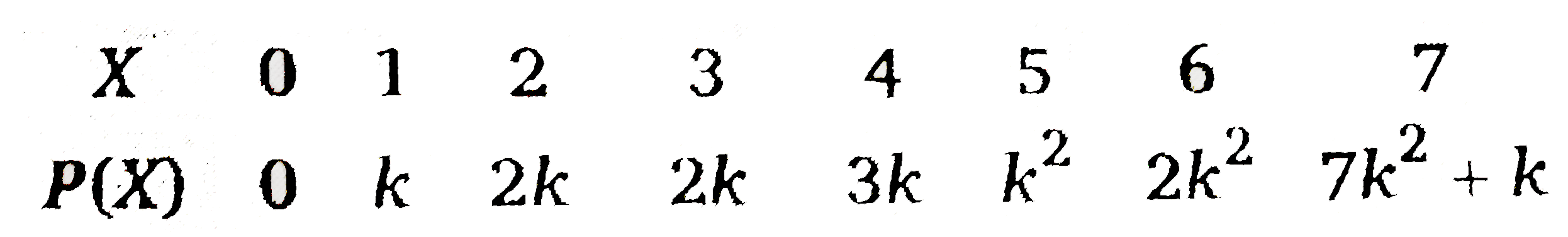
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution:
X: −2 −1 0 1 2 3
P(X):0.1 k 0.2 2k 0.3 k , find value of k
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionIf X is a random variable with probability distribution P(X=k)=(k+1)C2k,K=0,1,2,…. then find C.
View SolutionA random variable X has the following distribution
x:1234P(X=x):k23k25k27k2
The value of k is
View SolutionA random, variable X has the following probability distribution: X: 0 1 2 3 4 5 6 7 P(X):0 k 2k 2k 3k k2 2k2 7k2+k Find each of the following: i. k ii. P(X<6) iii. P(X≥6) iv. P(0<X<5)
View SolutionA discrete random variable X has the probability distribution given below: X: 0.5 1 1.5 2 P(X): k k2 2k2 k then, Find the value of k.
View SolutionA random variable X has the following distribution
X=x1:1234P(X=x1):k2k3k4k
The value of k and P(X<3) are equal to
View SolutionA random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
View SolutionA random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
View Solution
