द्विघात बहुपद f(x)=3−2x−x2 का आलेख खींचिये |
माना y=f(x) अथवा y=3−2x−x2

निम्न सारणी x के विभिन्न मानो के लिए बहुपद y=3−2x−x2 के विभिन्न मान दर्शाती है :
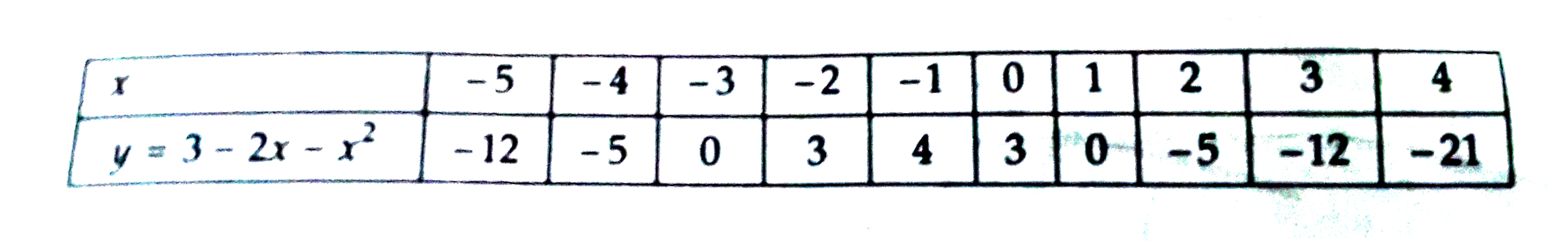
बिंदुओं (−5,−12),(−4,−5),(−3,0),(−2,3),(−1,4),(0,3),(1,0),(2,−5),(3,−12) और (4,−21) को आलेख पेपर पर अंकित करके इनसे गुजरने वाला वक्र खींचते है जो एक चित्र में दर्शाया गया है | स्पष्ट है कि यह एक परवलय के रूप में है | इस परवलय पर उच्चतम बिंदु P(−1,4) है जिसे परवलय का शीर्ष कहते है | शीर्ष से गुजरने वाली उर्ध्वाधर रेखा इस परवलय का अक्ष कहलाती है |
प्रेक्षण : हम बहुपद f(x)=3−2x−x2 के आलेख से निम्न निष्कर्ष निकलते है |
(i) बहुपद f(x)=3−2x−x2 में, x2 का गुणांक -1 है जो कि ऋणात्मक वास्तविक संक्ख्या है | अतः परवलय नीचे की ओर खुलता है |
(ii) बहुपद f(x)=3−2x−x2=(1−x)(x+3) के दो भिन्न- भिन्न रैखिक गुणनखंड (1−x) और (x+3) है | अतः परवलय दो विभिन्न बिंदुओं (1,0) और (−3,0) पर x - अक्ष को प्रतिच्छेद करता है | इन बिंदुओं के x - निर्देशांक f(x) के शून्यक है |
(iii) बहुपद f(x)=3−2x−x2 के - 3 और 1 दो भिन्न - भिन्न शून्यक है | अतः परवलय y=3−2x−x2 दो भिन्न - भिन्न बिंदुओं पर x - अक्ष को काटता है |
(iv) बहुपद 3−2x−x2 की तुलना ax2+bx+c से करने पर a=−1,b=−2 और c=3 प्राप्त करते है | परवलय का शीर्ष बिंदु (−1,4) अर्थात (−ba,−D4a) है, जहाँ D=b2−4ac है |
(v) D=b2−4ac=4+12=16>0 है | अतः परवलय x - अक्ष को दो भिन्न - भिन्न बिंदुओं पर प्रतिच्छेद करता है |
Topper's Solved these Questions
Similar Questions
इन द्विघात बहुपदों के शून्यक ज्ञात कीजिये और शून्यक तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जॉंच कीजिए :
f(x)=x2−2x−8
View Solutionसत्यापित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गयी संख्याएँ उनकी शून्यक है | प्रत्येक स्थिति में शुन्यकों और गुणांकों के बीच के सम्बन्ध को भी सत्यापित कीजिए :
(i) f(x)=2x3+x2−5x+2,12,1,−2
(ii) g(x)=x3−4x2+5x−2,2,1,1
View Solutionयदि अंको 1, 2,3,4,5,6,7,8,9 में से एक अंक यादृच्छया चुना जाता है, तो एक विषम अंक प्राप्त होने की प्राविकता है:
View Solutionएक 6 सेमी. त्रिज्या वाला वृत्त खींचिए। इसके केन्द्र से 10 सेमी. दूरी पर स्थित एक बिन्दु से वृत्त की स्पर्श रेखाएँ खींचिए तथा उनकी लम्बाई ज्ञात कीजिए।
View Solutionद्विघात बहुपद ax2+bx+c के आलेख की आकृति किस प्रकार की प्राप्त होती है?
View Solutionएक द्विघात बहुपद f(x), जो f(0)=0,f(1)=1,f'(x)>0, को सभी x∈(0,1) के लिए संतुष्ट करता है, है
View Solutionx = 2 का आलेख निरूपण ?
View Solutionद्विघात बहुपद x2+3x−(a+2)(a−1)के शून्यक हैं :,
View Solutiont2−5t+1=0 द्विघात बहुपद के शून्यकों का योगफल है:
View Solutiont2−5t+1=0 द्विघात बहुपद के शून्यको का गुणनफल है :
View Solutionद्विघात बहुपद x2−3के शून्यको का गुणनफल ज्ञात कीजिए।
View Solutionद्विघात x2−3x−4 बहुपद के शून्यको का गुणनफल ज्ञात कीजिए।
View Solutionद्विघात बहुपद x2+2x+3 के शून्यको का योग ज्ञात कीजिए।
View Solutionद्विघात बहुपद x2+7x+10 के शून्यको का योग ज्ञात कीजिए |
View Solution2x+3y>5 का आलेख खींचिए|
View Solutionयदि x=32, बहुपद 2x2+kx−12 का एक शून्यक है, तब k का मान है
View Solution
