बहुपद 3x2+2x−1=0 को हल कीजिए ।
माना y=f(x) अथवा y=−3x2+2x−1
x के विभिन्न मानो के लिए y के मान नीचे दी गयी सारणी में अंकित है |
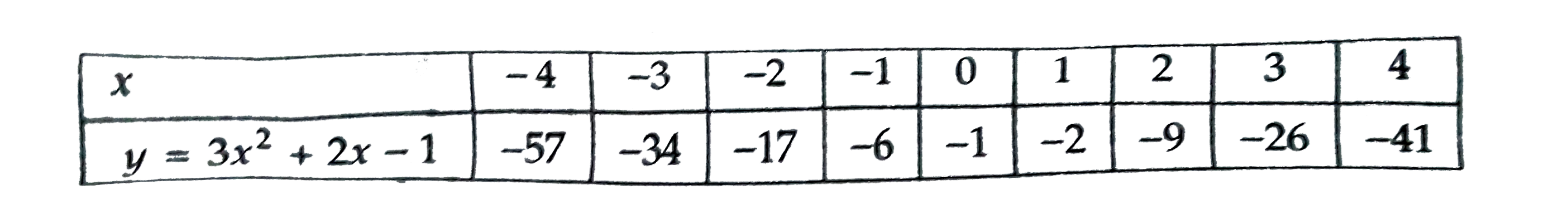
अतः y=−3x2+2x−1 का आलेख बिंदुओं (−4,−57),(−3,−34),(−2,−17),(−1,−6),(0,−1),(1,−2),(2,−9),(3,−26) और (4,−41) से होकर गुजरता है |
अब ग्राफ पेपर पर इन बिंदुओं को अंकित करके इनसे गुजरने वाला वक्र खींचते है | इस प्रकार प्राप्त वक्र चित्र में दर्शाया गया है |
प्रेक्षण : बहुपद f(x)=−3x2+2x−1 के आलेख से निम्न निष्कर्ष निकलते है |
(i) बहुपद f(x)=−3x2+2x−1 में x2 का गुणांक -3 , अर्थात ऋणात्मक वास्तविक संख्या है अतः परवलय नीचे की ओर खुलता है |
(ii) बहुपद f(x)=−3x2+2x−1 के गुणनखण्ड नहीं हो सकते है | अतः परवलय x - अक्ष को स्पर्श नहीं करता है और न ही x - अक्ष को काटता है |
(iii) बहुपद f(x)=−3x2+2x−1 के कोई वास्तविक शून्यक नहीं है इसलिए परवलय x - अक्ष को न तो स्पर्श करता है और न ही x - अक्ष को काटता है |
(iv) बहुपद f(x) के सभी मान ऋणात्मक है क्योंकि परवलय नीचे की ओर खुलता है और x - अक्ष के नीचे रहता है |
(v) बहुपद f(x)=−3x2+2x−1 की ax2+bx+c, से तुलना करने पर a=−3, और c=−1 पाते है | परवलय का शीर्ष (−b2a,−D4a) अर्थात (13,−23) है , जहाँ D=b2−4ac है |
Topper's Solved these Questions
Similar Questions
इन द्विघात बहुपदों के शून्यक ज्ञात कीजिये और शून्यक तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जॉंच कीजिए :
f(x)=x2−2x−8
View Solutionसत्यापित कीजिए कि निम्न त्रिघात बहुपदों के साथ दी गयी संख्याएँ उनकी शून्यक है | प्रत्येक स्थिति में शुन्यकों और गुणांकों के बीच के सम्बन्ध को भी सत्यापित कीजिए :
(i) f(x)=2x3+x2−5x+2,12,1,−2
(ii) g(x)=x3−4x2+5x−2,2,1,1
View Solutionयदि अंको 1, 2,3,4,5,6,7,8,9 में से एक अंक यादृच्छया चुना जाता है, तो एक विषम अंक प्राप्त होने की प्राविकता है:
View Solutionएक 6 सेमी. त्रिज्या वाला वृत्त खींचिए। इसके केन्द्र से 10 सेमी. दूरी पर स्थित एक बिन्दु से वृत्त की स्पर्श रेखाएँ खींचिए तथा उनकी लम्बाई ज्ञात कीजिए।
View Solutionनिम्न असमिकाओं निकाय को हल कीजिए -
y≥−2,y<−2
View Solutionनिम्न समीकरणों को हल कीजिए -
tan2θ=tan(2θ).
View Solutionवर्ग समीकरण 3x2+8ix+3=0 को हल कीजिए ।
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
हल कीजिए -
dydx=1x+y+1
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए -
(2x+y+1)dx+(4x+2y−1)dy=0
View Solutionनिम्नलिखित अवकल समीकरणों को हल कीजिए -
(2x−103)dydx+y=0
View Solutionहल कीजिए :
(2x+3y−5)(dy/dx)+(3x+2y−5)=0.
View Solutionनिम्न अवकल समीकरणों को हल कीजिए-
ydx−x dy+3x2y2ex3dx=0
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
dydx+3x−2y−52x+3y−5=0
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
(2x+y+1)dx+(4x+2y−1)dy=0
View Solutionनिम्नलिखित अवकलन समीकरणों को हल कीजिए-
dydx=1−3x−3y2(x+y)
View Solutionनिम्न को हल कीजिए
∣∣x2+4x+3∣∣+2x+5=0
View Solution
