$Δ A B C$ कि रचना करो जिसमे AB = 4 सेमी., BC = 5 सेमी. और AC = 6 सेमी. है। $Δ A B C$ के समरूप एक त्रिभुज की रचना करो जिसकी प्रत्येक भुजा $Δ A B C$ की संगत भुजा की दो-तिहाई (2/3) rd हो। अपने कथन के औचित्य को सिद्ध भी कीजिए।

Text Solution

Verified by Experts

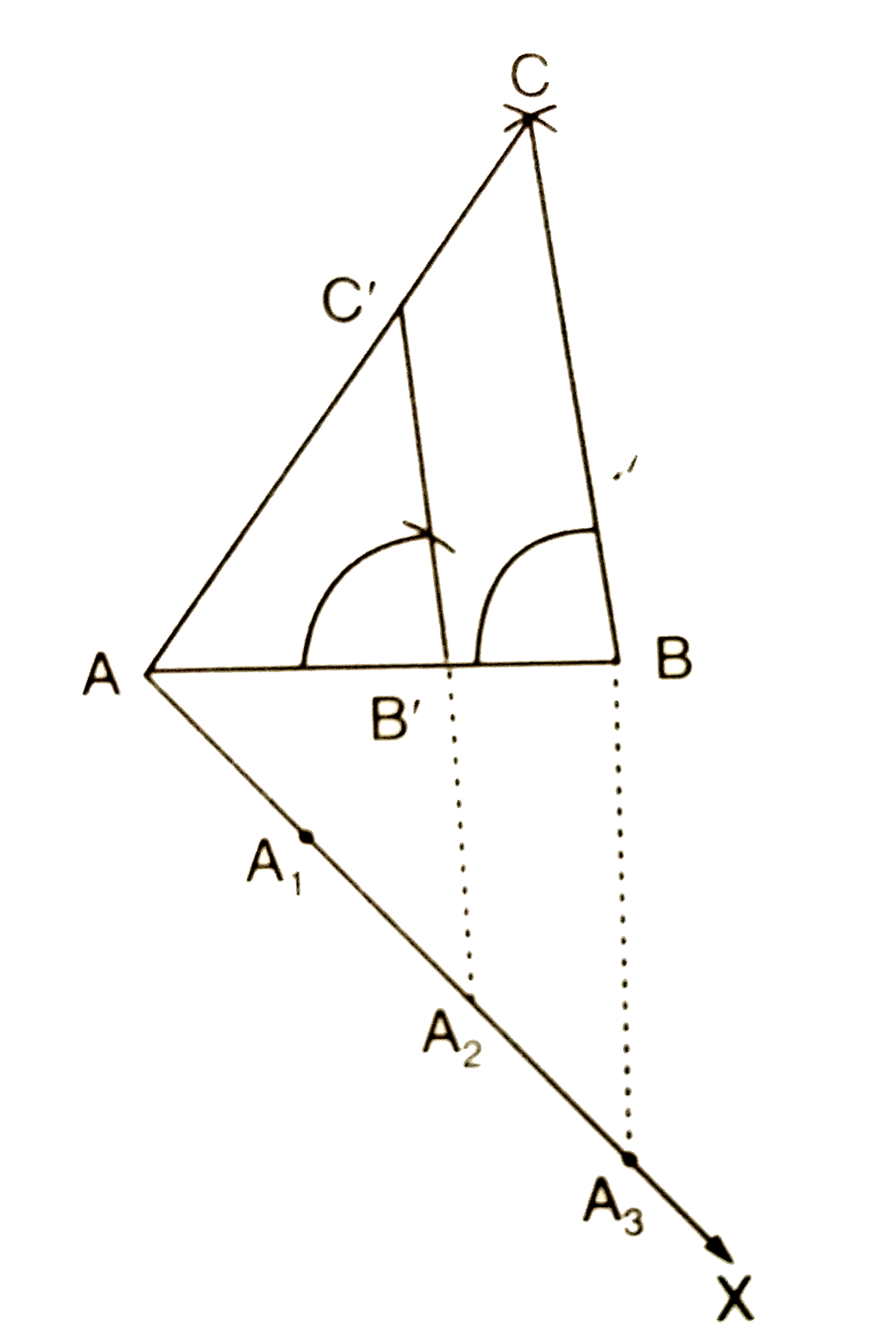
रचना के चरण
चरण I 4 सेमी. लम्बा रेखाखण्ड AB खींचिए।
चरण II A को केन्द्र मानकर AC = 6 सेमी. त्रिज्या का एक चाप खींचिए जो AC को C' पर काटता है।
चरण III B को केन्द्र मानकर BC = 5 सेमी. त्रिज्या का एक दूसरा चाप खींचिए जो प्रथम चाप को C पर प्रतिच्छेद करता है।
चरण IV $Δ A B C$ प्राप्त करने के लिए AC और BC को मिलाइए।
चरण V AB से नीचे, एक न्यून कोण $∠ B A X$ बनाओं।
चरण VI भुजा AX पर तीन बिन्दु $A_{1}, A_{2}, A_{3},$ इस प्रकार अंकित करो कि $A A_{1} = A_{1} A_{2} = A_{2} A_{3}$ हो।
चरण VII $A_{3} B$ को मिलाइए।
चरण VIII चूँकि हमे इस एक ऐसे त्रिभुज की रचना करनी है जिसकी प्रत्येक भुजा $Δ A B C$ की संगत भुजा की दो-तिहाई हो। अतः AX पर अंकित तीन बराबर भागो में से दो भाग लीजिए। अर्थात $A_{2}$ से $A_{2} B' ∣ ∣ A_{3} B$ खींचिए।
चरण IX B' से B'C'||BC खींचिए जो AC को C' पर मिलती है। इस प्रकार प्राप्त त्रिभुज AB'C' अभीष्ट त्रिभुज है जिसकी प्रत्येक भुजा $Δ A B C$ की संगत भुजा की दो तिहाई है।
प्रतिपादन: चूँकि $B' C' ∣ ∣ B C$ है।
अतः $Δ A B C ~ Δ A B' C'$
$∴ \frac{B' C'}{B C} = \frac{A C'}{A C} = \frac{A B'}{A B} = \frac{2}{3} [∵ \frac{A B'}{A B} = \frac{2}{3}]$
(ii) माना $Δ A B C$ दिया गया त्रिभुज है। $Δ A B C$ हमे के समरूप एक ऐसे त्रिभुज की रचना करनी है जिसकी प्रत्येक भुजा $Δ A B C$ की संगत भुजा ${(m / n)}^{t h}$ इस प्रकार हो कि $m > n$ है। अभीष्ट त्रिभुज प्राप्त करने के लिए हमे निम्न क्रमबद्ध प्रक्रिया का उपयोग करेंगे।
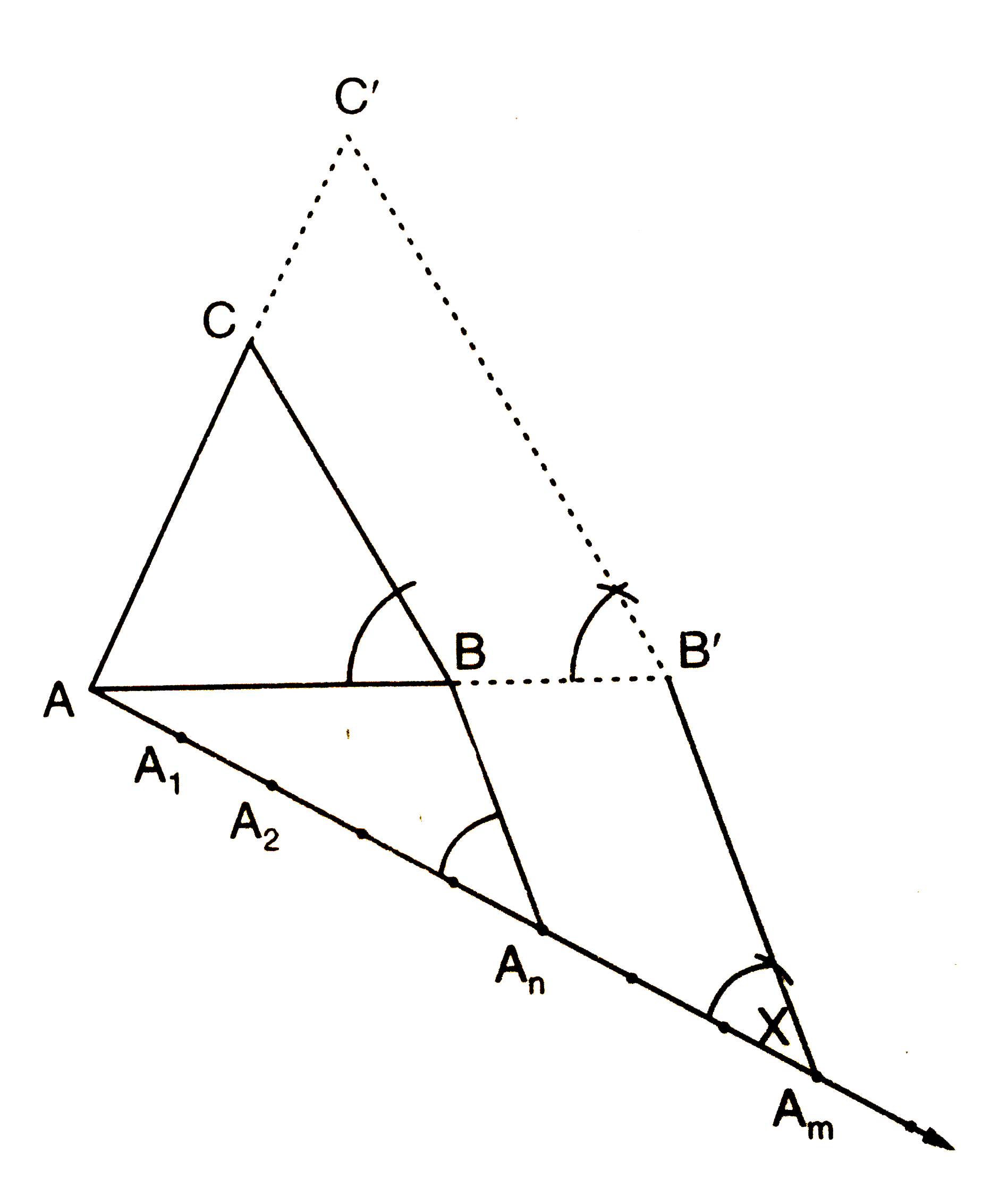
रचना के चरण
चरण I दिये गये आँकड़ों की सहायता से त्रिभुज की रचना कीजिए।
चरण II दिये गये त्रिभुज की तीनो भुजाओं में से किसी भुजा को आधार मान लीजिए। माना AB दिये गये त्रिभुज का आधार है।
चरण III आधार AB के एक सिरे (माना A) पर एक न्यून कोण $∠ B A X$ ,AB से नीचे की और अर्थात शीर्ष C के विपरीत बनाओं।
चरण IV AX पर m (m और n से बड़ा) बिन्दु $A_{1}, A_{2}, ..., A_{m}$ इस प्रकार अंकित करो कि $A A_{1} = A_{1} A_{2} = ... = A_{m - 1} A_{m}$
चरण V बिन्दु $A_{n}$ को B से मिलाओं तथा $A_{n} B$ के समानांतर बिन्दु $A_{m}$ से एक रेखा खींचो जो बढ़ी हुई रेखाखण्ड AB को B' पर काटे।
चरण VI BC के समानान्तर बिन्दु B' से एक रेखा खींचो जोकि बढ़ी हुई रेखाखण्ड AC को C' पर काटे।
चरण VII इस प्रकार प्राप्त $Δ A B' C'$ अभीष्ट त्रिभुज है।
प्रतिपादन: उपर्युक्त रचना के औचित्य को सिद्ध करने के लिए त्रिभुज ABC और AB'C' पर विचार करते है। त्रिभुज ABC और AB'C' में
$∠ B A C = ∠ B' A C'$
$∠ A B C = ∠ A B' C' [∵ B' C' || B C]$
अतः समरूपता की AA कसौटी से
$Δ A B C ~ Δ A B' C'$
$\Rightarrow \frac{A B}{A B'} = \frac{B C}{B' C'} = \frac{A C}{A C'} ... (i)$
$Δ A A_{m} B'$ में
$A_{n} B || A_{m} B'$
$∴ \frac{A B}{B B'} = \frac{A A_{n}}{A_{n} A_{m}}$
$\Rightarrow \frac{B B'}{A B} = \frac{A_{n} A_{m}}{A A_{n}}$
$\Rightarrow \frac{B B'}{A B} = \frac{m - n}{n}$
$\Rightarrow \frac{A B' - A B}{A B} = \frac{m - n}{n}$
$\Rightarrow \frac{A B'}{A B} - 1 = \frac{m - n}{n}$
$\Rightarrow \frac{A B'}{A B} = \frac{m}{n} ... (ii)$
(i) व (ii) से,
$\frac{A B'}{A B} = \frac{B' C'}{B C} = \frac{A C'}{A C} = \frac{m}{n}$

|

Updated on:21/07/2023

Class 10 MATHS CONSTRUCTIONS

Topper's Solved these Questions

Similar Questions

RD SHARMA-रचनाएँ-प्रश्नावली 11.3

Home
Ask Doubt
Profile