In triangle ABC, the length of BC is less than twice the length of AB by 2 cm. The length of AC exceeds the length of AB by 10 cm. The perimeter is 32 cm. The length (in cm) of the smallest side of the triangle is :
त्रिभुज ABC में, BC की लंबाई AB की लंबाई के दोगुने से 2 कम है | AC की लंबाई AB की
लंबाई से 10 सेमी अधिक है | परिमाप 32 सेमी है | त्रिभुज की सबसे छोटी भुजा की लंबाई है -
4
10
8
6
To solve the problem, we will define the lengths of the sides of triangle ABC based on the information given in the question.
1. Define the variables:
- Let the length of side AB be x cm.
- According to the problem, the length of side BC is less than twice the length of AB by 2 cm. Therefore, we can express BC as:
BC=2x−2 cm
- The length of side AC exceeds the length of AB by 10 cm, so we can express AC as:
AC=x+10 cm
2. Set up the perimeter equation:
- The perimeter of triangle ABC is given as 32 cm. The perimeter can be expressed as the sum of the lengths of the sides:
AB+BC+AC=32
- Substituting the expressions for BC and AC into the perimeter equation, we get:
x+(2x−2)+(x+10)=32
3. Simplify the equation:
- Combine like terms:
x+2x−2+x+10=32
4x+8=32
4. Solve for x:
- Subtract 8 from both sides:
4x=32−8
4x=24
- Divide both sides by 4:
x=6 cm
5. Calculate the lengths of all sides:
- Now that we have x, we can find the lengths of BC and AC:
- Length of AB (x): 6 cm
- Length of BC:
BC=2(6)−2=12−2=10 cm
- Length of AC:
AC=6+10=16 cm
6. Identify the smallest side:
- The lengths of the sides are:
- AB = 6 cm
- BC = 10 cm
- AC = 16 cm
- The smallest side of triangle ABC is AB which is 6 cm.
Thus, the length of the smallest side of the triangle is 6 cm.
- Let the length of side AB be x cm.
- According to the problem, the length of side BC is less than twice the length of AB by 2 cm. Therefore, we can express BC as:
BC=2x−2 cm
- The length of side AC exceeds the length of AB by 10 cm, so we can express AC as:
AC=x+10 cm
- The perimeter of triangle ABC is given as 32 cm. The perimeter can be expressed as the sum of the lengths of the sides:
AB+BC+AC=32
- Substituting the expressions for BC and AC into the perimeter equation, we get:
x+(2x−2)+(x+10)=32
- Combine like terms:
x+2x−2+x+10=32
4x+8=32
- Subtract 8 from both sides:
4x=32−8
4x=24
- Divide both sides by 4:
x=6 cm
- Now that we have x, we can find the lengths of BC and AC:
- Length of AB (x): 6 cm
- Length of BC:
BC=2(6)−2=12−2=10 cm
- Length of AC:
AC=6+10=16 cm
- The lengths of the sides are:
- AB = 6 cm
- BC = 10 cm
- AC = 16 cm
- The smallest side of triangle ABC is AB which is 6 cm.
Topper's Solved these Questions
Similar Questions
In triangle ABC, the length of BC is less than twice the length of AB by 2 cm. The length of AC exceeds the length of AB by 10 cm. The perimeter is 32 cm. The length (in cm) of the smallest side of the triangle is :
त्रिभुज ABC में, BC की लंबाई AB की लंबाई के दोगुने से 2 कम है | AC की लंबाई AB की लंबाई से 10 सेमी अधिक है | परिमाप 32 सेमी है | त्रिभुज की सबसे छोटी भुजा की लंबाई है -
View SolutionIn triangle ABC, the length BC is less than twice the length of AB by 3 cm. The length of AC exceeds the length of AB by 9 cm. The perimeter of the triangle is 34 cm. The length (in cm) of the smallest side of the triangle is
त्रिभुज ABC में, BC की लंबाई AB की लंबाई के दोगुने से 3 सेमी कम है| AC की लंबाई AB की लंबाई से 9 सेमी अधिक है | त्रिभुज का परिमाप 34 सेमी है | त्रिभुज की सबसे छोटी भुजा की लंबाई है -
View Solution
Knowledge Check
△ABC is an isosceles triangle with AB=AC=15cm and altitude from A to BC is 12 cm. The length of sides BC is :
A9 cmB12 cmC18 cmD20 cmIn a △ABC,AB = 10 cm, BC = 12 cm and AC = 14 cm. Find the length of median AD. If G is the centroid, find length of GA.
A53√7,59√7B5√7,4√7C10√3,83√7D4√7,83√7In △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :
A√3172cmB√1192cmC√1152cmD√3132cm
In triangle ABC, the length of BC is less than twice the length of AB by 3 cm. The length of the AC exceeds the length of AB by 1 cm. The perimeter of the triangle is 34 cm. The length (in cm) of the smaller side of the triangle is :
त्रिभुज ABC में, BC की लंबाई AB की लंबाई के दोगुने से 3 सेमी कम है| AC की लंबाई AB की लंबाई से 1 सेमी अधिक है | त्रिभुज का परिमाप 34 सेमी है |त्रिभुज की छोटी भुजा की लंबाई (सेमी में ) ज्ञात करें |
View SolutionIn triangle ABC, the length of BC is less than twice the length of AB by 3 cm. The length of the AC exceeds the length of AB by 1 cm. The perimeter of the triangle is 34 cm. The length (in cm) of the smaller side of the triangle is :
त्रिभुज ABC में, BC की लंबाई AB की लंबाई के दोगुने से 3 सेमी कम है | AC की लंबाई AB की लंबाई से 1 सेमी अधिक है | त्रिभुज का परिमाप 34 सेमी का है | त्रिभुज की छोटी भुजा की लंबाई ( सेमी में ) ज्ञात करें |
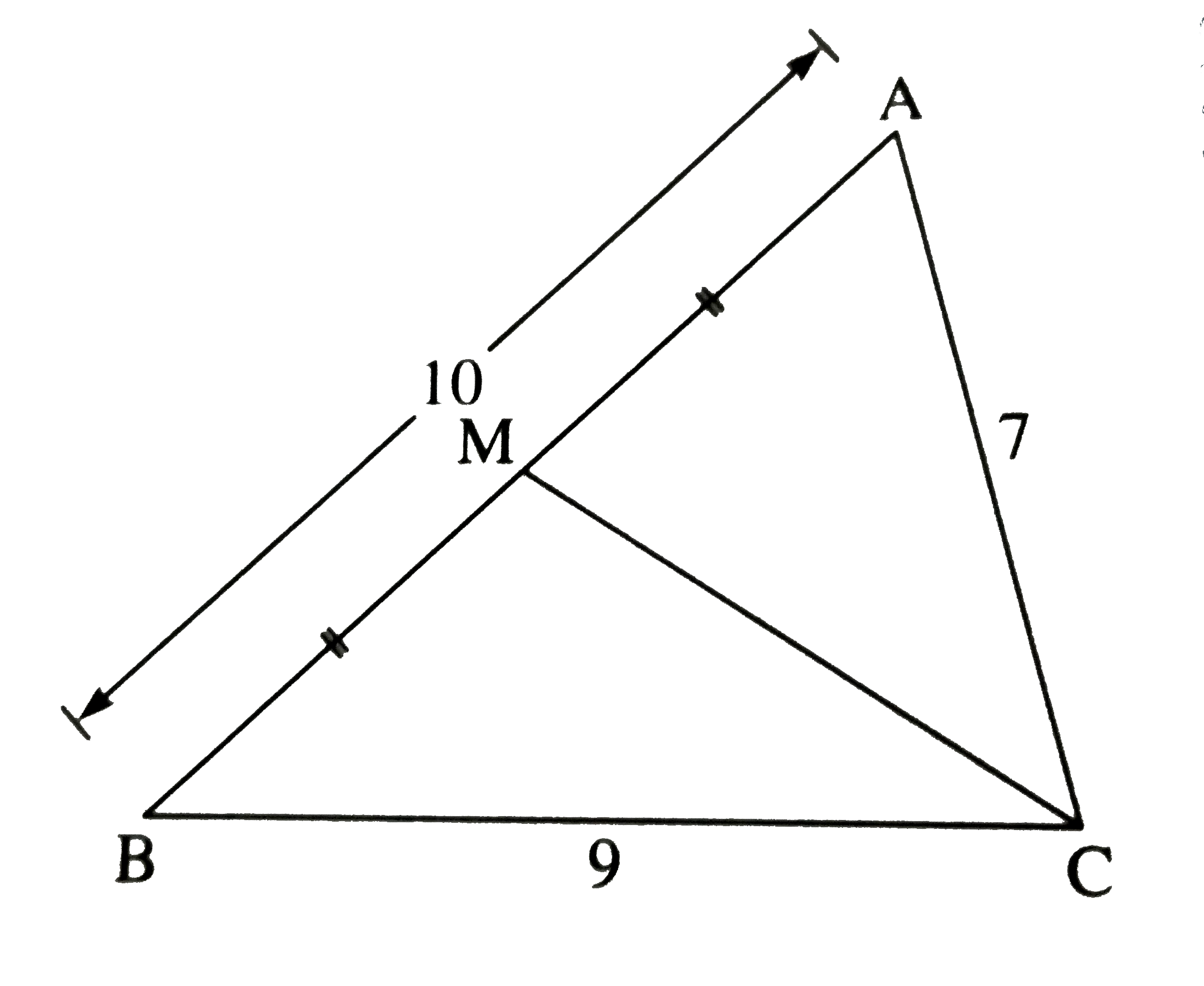
View SolutionIn △ABC , AB=10
AC=7,BC=9
then find the length find the length of the median drawn from point C to side AB .
View SolutionIn a triangle ABC the angle A is twice the angle C, the side BC is 2 cm longer than the side AB, and AC=5 cm. Find AB and BC.
View SolutionIn a triangle ABC, AB =AC and the perimeter of A ABC is 8(2+√2) cm . If the length of BC is √2 times the length of AB, then find the area of △ABC.
एक त्रिभुज ABC में AB = AC और △ABC की परिधि 8(2+√2) सेमी है। यदि 80 की लंबाई AB की लंबाई से √2 गुना है, तो △ABC का क्षेत्रफल ज्ञात कीजिए|
View Solution
