सिद्ध कीजिए कि किसी समान्तर चतुर्भुज की सम्मुख भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड, इसे दो बराबर समान्तर चतुर्भुजों में विभाजित करता है।
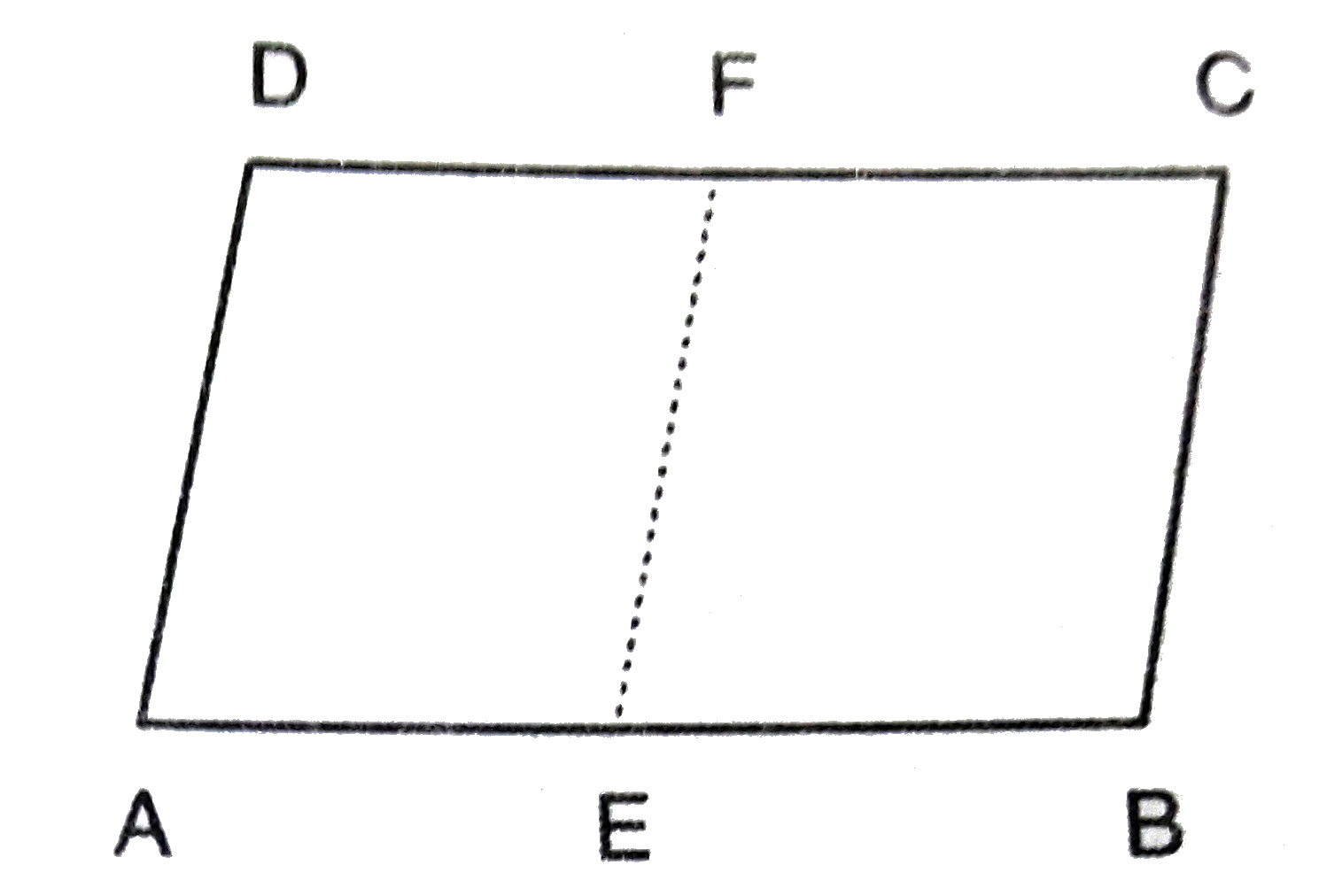
दिया है : एक समान्तर चतुर्भुज ABCD जिसकी भुजाओं AB तथा CD के मध्य-बिंदु क्रमशः E तथा F हैं।
सिद्ध करना है : ar(||gmAEFD)=ar(||gmEBCF)
रचना : EF को मिलाइये ।
उत्पत्ति: चूँकि ABCD एक समान्तर चतुर्भुज है।
∴ AB || DC तथा AB = DC
⇒ AE || DF तथा 12AB=12DC
⇒ AE || DF तथा AE = DF [∵E तथा F क्रमशः AB तथा CD के मध्य-बिंदु है।∴AE=12AB तथा DF=12DC]
अतः चतुर्भुज AEFD में सम्मुख भुजाओं AE तथा DF का एक युग्म बराबर तथा समान्तर है।
∴ AEFD एक समान्तर चतुर्भुज है।
इसी प्रकार EBCF एक समान्तर चतुर्भुज है।
अब AEFD तथा EBCF बराबर आधारों AE तथा EB और एक ही समान्तर रेखाओं AB तथा DC के बीच स्थित समान्तर चतुर्भुज है।
∴ar(||gmAEFD)=ar(||gmEBCF)
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - व्याख्यात्मक उदाहरण
1 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 15.1
6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण BOOK - RD SHARMACHAPTER - संख्यिकीय आंकड़ों का आलेखीय निरूपण EXERCISE - बहु विकल्पीय प्रश्न
8 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - बहु विकल्पीय प्रश्न
17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionयदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित करने वाले सदिश ¯a,¯b,¯c,¯d हों तों सिद्ध कीजिए कि चतुर्भुज एक समांतर चतुर्भुज होगा यदि और केवल यदि ¯a+¯c=¯0 जिससे ¯b+¯d=¯0
View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
View Solutionसिद्ध कीजिए की किसी विषम पदों वाली समांतर श्रेढ़ी का योगफल श्रेढ़ी में माढ्य पद और पदों की संख्या के गुणगंफल के बराबर होता है |
View Solutionसिद्ध कीजिए कि बिंदुओं (2,3) और(3,4) को मिलाने वाले रेखाखण्ड के मध्य बिंदु के निर्देशांक x और y निम्नलिखित समीकरण को संतुष्ट करते है :
x−y+1=0.
View Solutionकिसी त्रिभुज के शीर्ष बिन्दुओं के निर्देशांक (0,1),(2,0) और (-1,-2) है। उसकी भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionबिन्दुओं (2,3) और (4,5) को मिलाने वाला रेखाखण्ड बिन्दुओं (-3,4) और (-1,-2) को मिलाने वाली रेखा द्वारा किस अनुपात में विभाजित होता है?
View Solutionबिन्दुओं (3,4) और (7,8) को मिलाने वाले रेखाखण्ड को रेखा 2x+3y+7=0 किस अनुपात में विभक्त करती है?
View Solutionपरवलय y2=4px की किसी द्विकोटि की लम्बाई 8p है। सिद्ध कीजिए कि शीर्ष को उसके सिरों से मिलाने वाली सरल रेखाएँ परस्पर लम्ब है।
View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionपरवलय y=x2−2x+5 की जीवा दो बिन्दुओं जिनकी कोटि है, x1=1,x2=3 को जोड़ती है, तो इस जीवा के है, को जोड़ती है , तो इस जीवा के समान्तर परवलर की स्पर्श रेखा का समीकरण होगा
View Solution
