Question

दर्शाए कि समान्तर चतुर्भुज के विकर्ण उसे चार बराबर क्षेत्रफल वाले त्रिभुजों में विभाजित करते है ।

Explanation

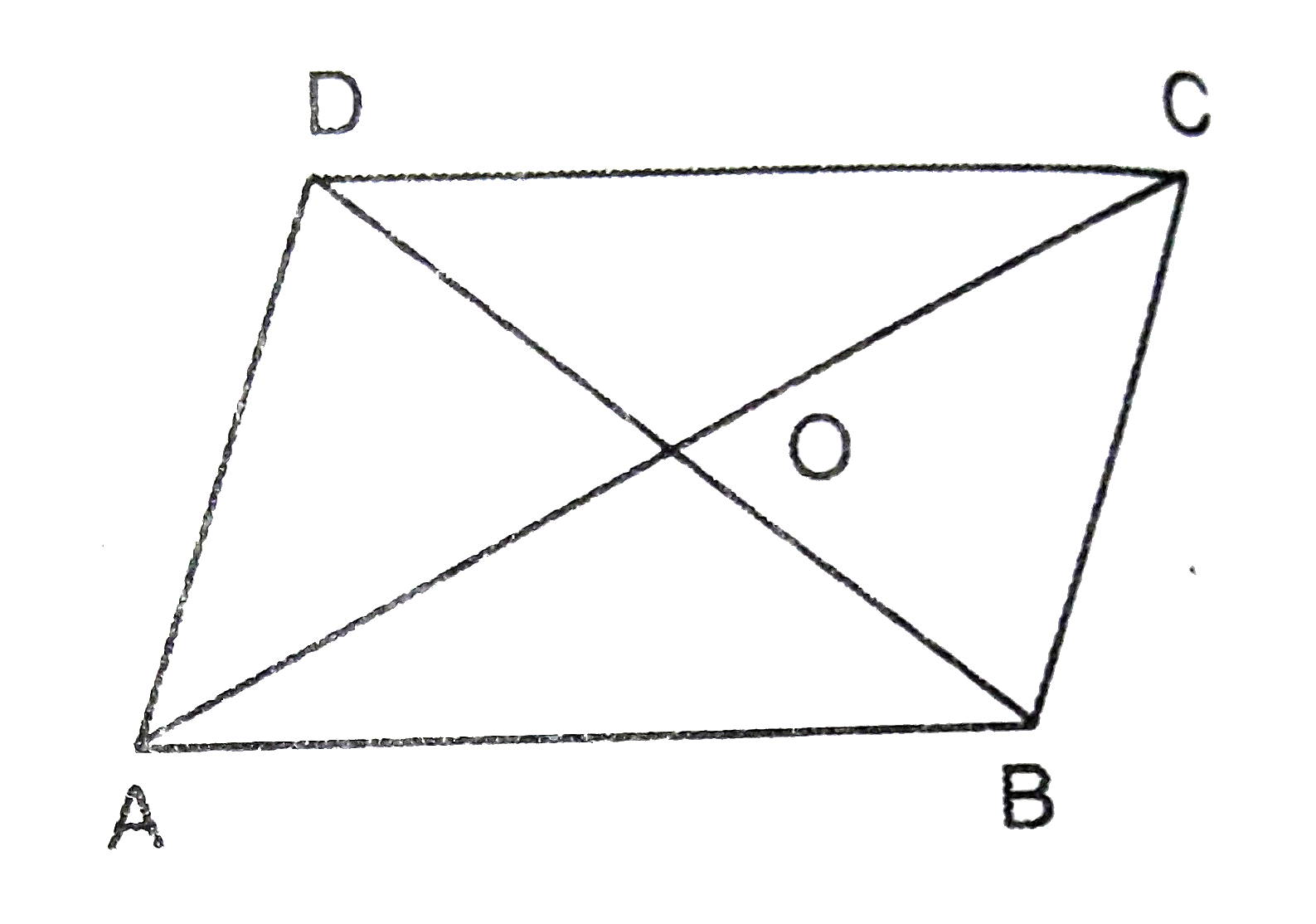
दिया है : एक समान्तर चतुर्भुज ABCD जिसके विकर्ण AC तथा BD बिंदु O पर प्रतिच्छेद करते है।
सिद्ध करना है : `ar(DeltaOAB) = ar(DeltaOBC) = ar(DeltaOCD)=ar(DeltaAOD)`
उपपत्ति : चूँकि समान्तर चतुर्भुज के विकर्ण प्रतिच्छेद बिंदु पर परस्पर समद्विभाजित होते है।
`therefore OA = OC` तथा `OB=OD`
साथ ही, त्रिभुज की माध्यिका इसे दो बराबर त्रिभुजों में विभाजित करती है।
चूँकि `DeltaABC` में, BO इसकी माध्यिका है।
`therefore ar(DeltaOAB)=ar(DeltaOBC) " " ` ...(i)
`therefore BCD ` में, CO माध्यिका है।
`therefore ar(DeltaOBC) =ar(DeltaOCD) " " ` ...(ii)
`DeltaACD` में, DO माध्यिका है।
`therefore ar(DeltaOCD ) = ar(DeltaOAD) " " ` ...(iii)
(i), (ii) तथा (iii)
`ar(DeltaOAB)=ar(DeltaOBC)=ar(DeltaOCD)=ar(DeltaOAD)`