Question

यदि किसी चतुर्भुज का प्रत्येक विकर्ण इसे दो बराबर क्षेत्रफल वाले त्रिभुजों में विभाजित करता है, तो प्रदर्शित कीजिए कि यह चतुर्भुज एक समान्तर चतुर्भुज है ।

Explanation

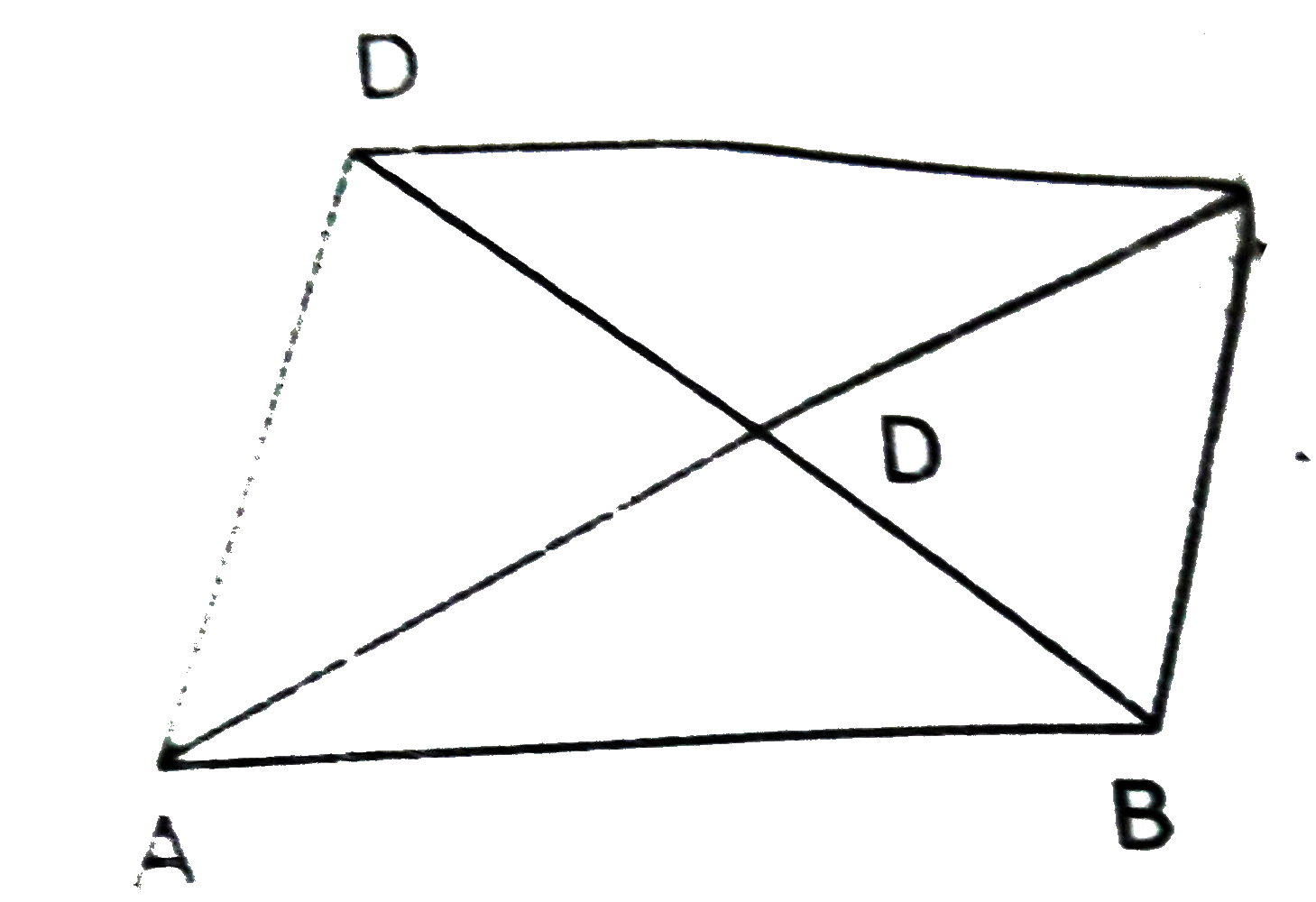
एक चतुर्भुज ABCD जिसके विकर्ण AC तथा BD इस प्रकार है, कि
`ar(DeltaABD) = ar(DeltaCDB)` तथा `ar(DeltaABC) = ar(DeltaACD)`
सिद्ध करना है : चतुर्भुज ABCD एक समान्तर चतुर्भुज है।
उपपत्ति : चूँकि चतुर्भुज ABCD का विकर्ण AC इसे दो बराबर क्षेत्रफल वाले त्रिभुजों में बाँटता है।
`therefore ar(DeltaABC) = ar(DeltaACD) " " ` ...(i)
परन्तु, `ar(DeltaABC)+ar(DeltaACD)=ar` (चतुर्भुज ABCD )
`rArr 2ar(DeltaABC)=ar` (चतुर्भुज ABCD )` " " `[(i) से ]
`rArr ar(DeltaABC)=(1)/(2)ar`(चतुर्भुज ABCD )` " " `... (ii)
चूँकि `squareABCD` का विकर्ण BD इसे दो बराबर क्षेत्रफल वाली त्रिभुजों में विभाजित करता है।
`therefore ar(DeltaABD)=ar(DeltaBCD) " " ` ...(iii)
परन्तु `ar(DeltaABD)+ar(DeltaBCD)=ar`(चतुर्भुज ABCD )
`rArr 2ar(DeltaABD)=ar` (चतुर्भुज ABCD )` " "` [(iii) से]
`rArr ar(DeltaABD )=(1)/(2)ar` (चतुर्भुज ABCD )`" "` ...(iv)
( ii) तथा (iv) से
`ar(DeltaABC)=ar(DeltaABD)`
चूँकि `DeltaABC ` तथा `DeltaABD ` एक ही आधार AB पर स्थित है । इसलिए उनके संगत शीर्षलम्ब भी अवश्य बराबर होंगे। अर्थात
`DeltaABC` का C से खींचा ज्ञात शीर्षलम्ब
`rArr` DC ।। AB
इसी प्रकार AD ।। BC
अतः चतुर्भुज ABCD एक समान्तर चतुर्भुज है।