सिद्ध कीजिए, कि किसी समबाहु त्रिभुज का क्षेत्रफल $(\frac{\sqrt{3}}{4}) a^{2}$ होता है, जहाँ a त्रिभुज की भुजा की माप है।

Video Solution

Text Solution

Verified by Experts

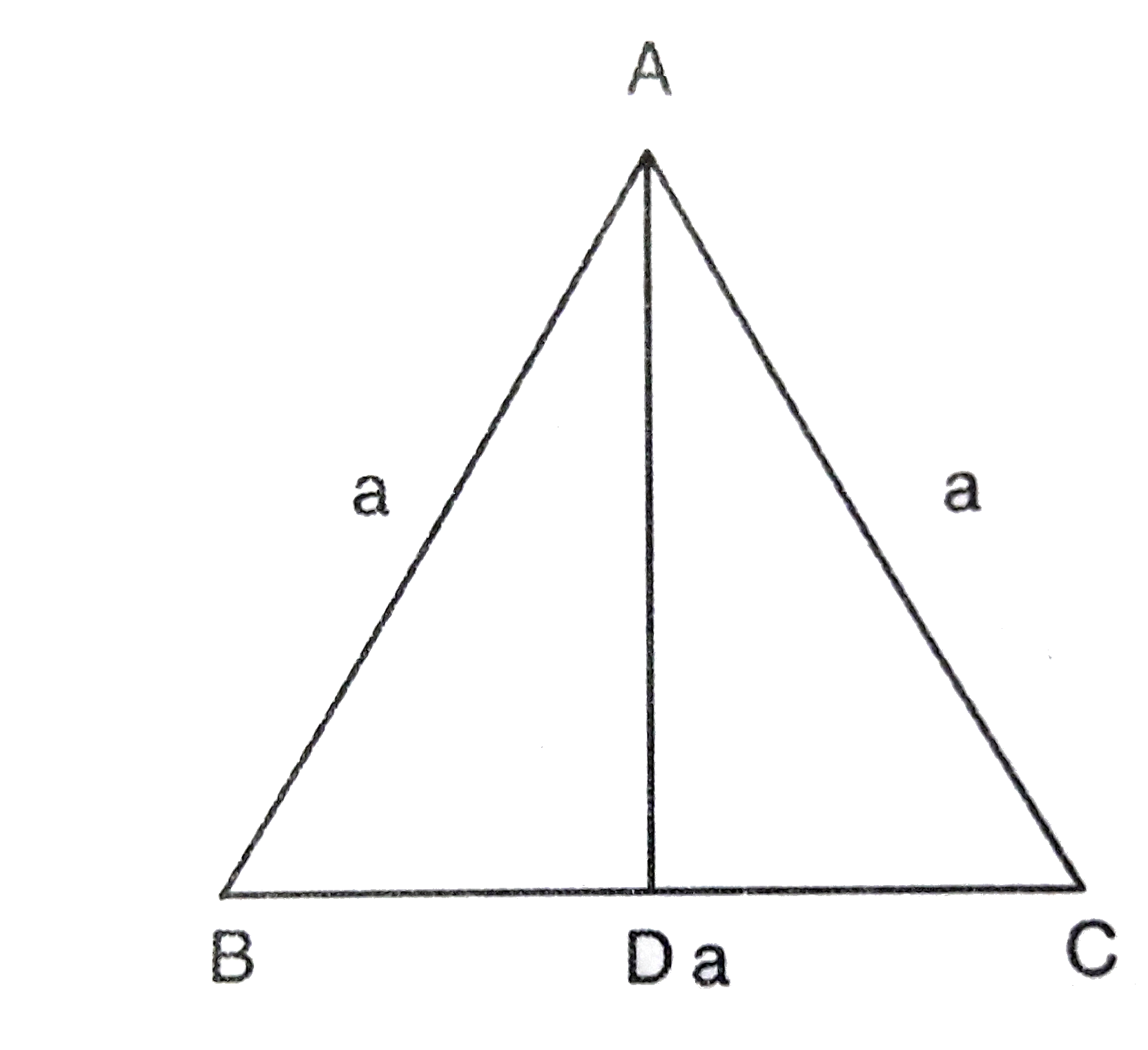
दिया है : एक समबाहु त्रिभुज ABC जिसमें $A B = B C = C A = a$ .
सिद्ध करना है : $a r (Δ A B C) = \frac{\sqrt{3}}{4} a^{2}$
रचना: $A D ⊥ B C$ खींचिये।
उपपत्ति: $Δ A B D$ तथा $Δ A C D$ में
$A B = A C$ [ $∵ Δ$ ABC समबाहु त्रिभुज है ]
$∠ A D B = ∠ A D C$ [ प्रत्येक कोण $90^{\circ}$ ]
तथा $A D = A D$ [उभयनिष्ठ भुजा]
अतः समकोण-विकर्ण-भुजा सर्वांगसमता कसौटी से
$Δ A B D ≅ Δ A C D$
$\Rightarrow B D = D C$
परन्तु $B D + D C = a \Rightarrow B D = D C = \frac{a}{2}$
समकोण त्रिभुज ABD में
$A B^{2} = A D^{2} + B D^{2}$ [ पाइथागोरस प्रमेय का प्रयोग करने पर]
$\Rightarrow a^{2} = A D^{2} + {(\frac{a}{2})}^{2}$
$\Rightarrow A D^{2} = a^{2} - \frac{a^{2}}{4} \Rightarrow A D^{2} = \frac{3 a^{2}}{4} \Rightarrow A D = \frac{\sqrt{3} a}{2}$
$∴ a r (Δ A B C) = \frac{1}{2} (B C \times A D)$
$\Rightarrow = \frac{1}{2} (a \times \frac{\sqrt{3}}{2} a) = \frac{\sqrt{3}}{a} a^{2}$

|

Updated on:21/07/2023

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

Similar Questions

RD SHARMA-समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल -बहु विकल्पीय प्रश्न

Home
Ask Doubt
Profile