यदि α,β बहुपद x2+2x+1 के शून्यक है, तब 1α+1β=
2
-2
0
1
The correct Answer is:B
Step by step video, text & image solution for यदि alpha, beta बहुपद x^(2)+2x+1 के शून्यक है, तब (1)/(alpha)+(1)/(beta)= by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - बहुपद EXERCISE - उदाहरण52videos
बहुपद
- BOOK - KC SINHACHAPTER - बहुपद EXERCISE - अभ्यास 2.118videos
बहुपद
- BOOK - KC SINHACHAPTER - बहुपद EXERCISE - दीर्घ उत्तरीय प्रश्न5videos
बहुपद
- BOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - वस्तुनिष्ठ प्रश्न54videos
प्रायिकता या सम्भावित
- BOOK - KC SINHACHAPTER - रचनाएँ EXERCISE - अभ्यास 11.114videos
रचनाएँ
Similar Questions
निचे दिया गया बहुपद के आलेख को देखकर बतायें कि ये एक-घातीय है या द्विघातीय है अथवा न एक-घातीय है और न द्विघातीय |
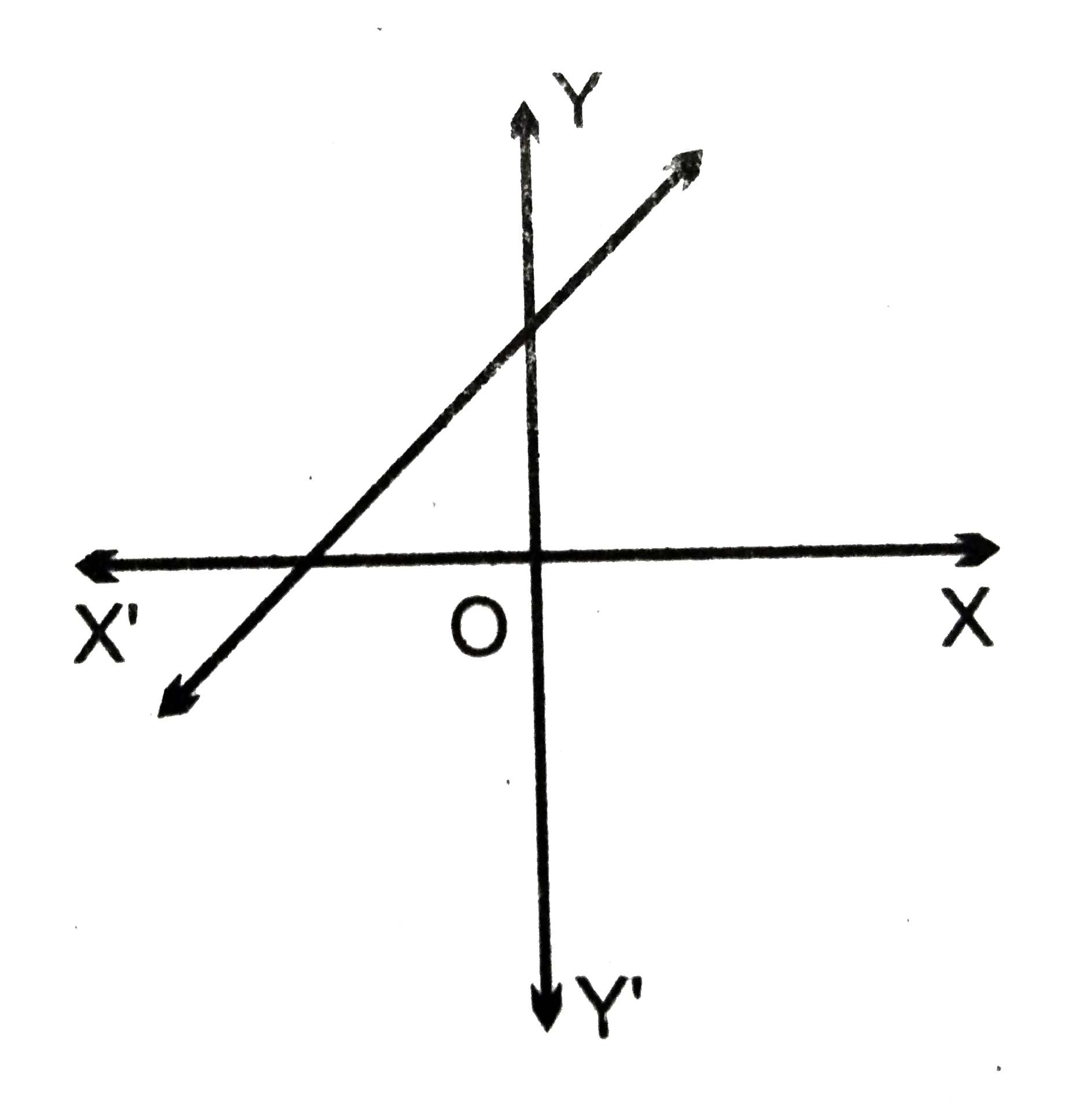 04:24View Solution
04:24View Solutionनीचे दिया गया बहुपद के आलेख को देखकर जाँच करें कि यह एक घातीय है या द्विघातीय या न तो एक घातीय है और न द्विघातीय |
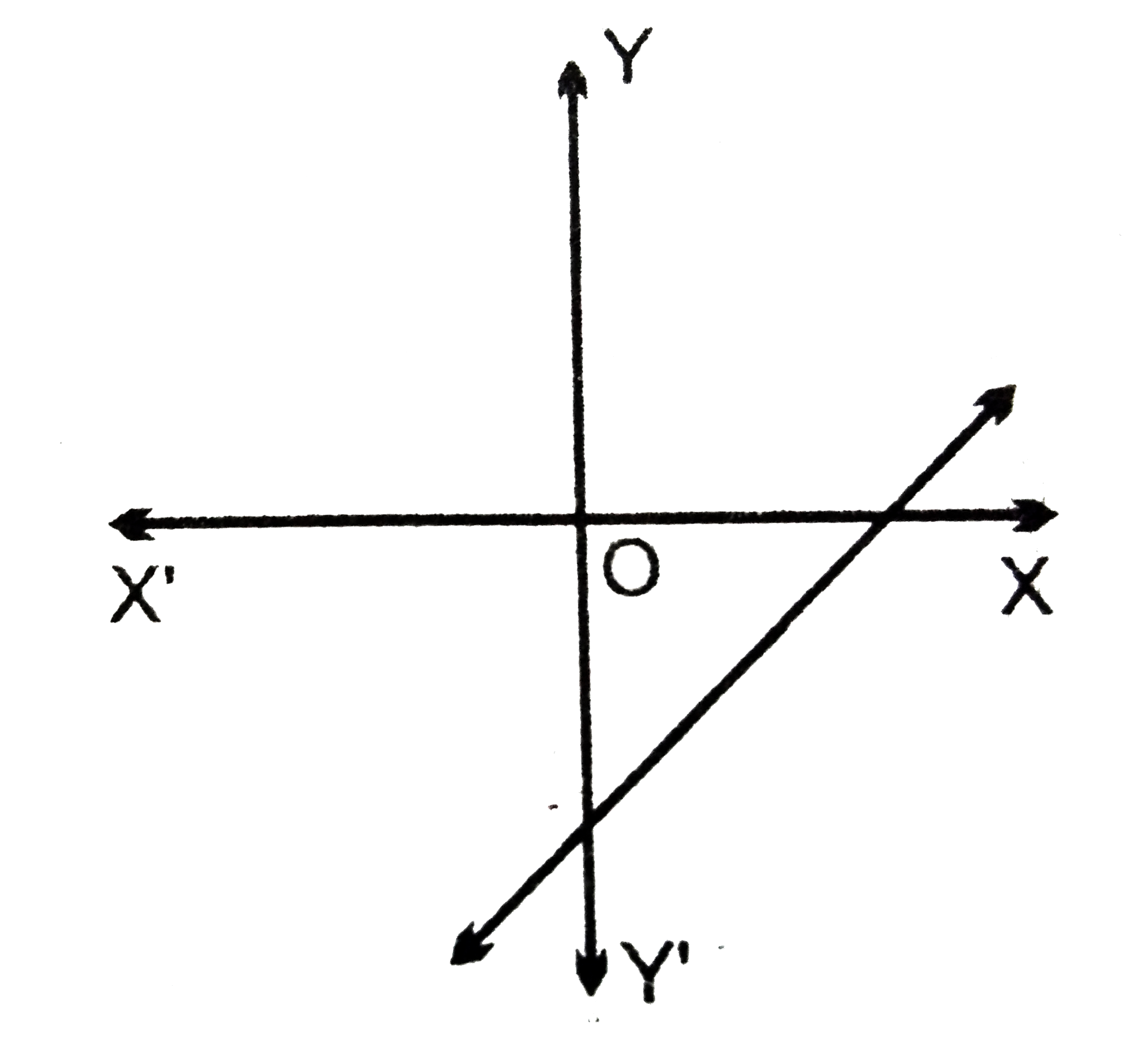 06:09View Solution
06:09View Solutionयदि p(x)=x3+kx2+hx+6और x+1 तथा x−2,p(x) के गुणनखण्ड है तो h और k का मान ज्ञात करे।
02:31View Solutionदो सिक्के उछालने में दो पट आने के प्रायिकता है:
05:41View Solution5.6 cm लम्बा एक रेखाखण्ड खींचे और इसे 5:8 के अनुपात में अतः विभक्त करें | दोनों भागो को मापे |
05:00View SolutionIf alpha and beta are roots of x^(2)-2x+3=0, then the equation whose roots are (alpha-1)/(alpha+1) and (beta-1)/(beta+1) will be
06:40View SolutionIF αandβ are the roots of 2x2+x+3=0 , then the equation whose roots are 1−α1+αand1−β1+β is
04:04View SolutionIf α,β,γ are roots of x3+2x2−1=0 then 1α+1β+1γ=
04:48View SolutionIf α and β are roots of x2+px+2=0 and 1α,1β are the roots of 2x2+2qx+1=0. Find the value of (alpha-1/alpha)(beta-1/beta)(alpha+1/beta)(beta+1/alpha)1
04:15View Solutionयदि समीकरण x2−2x+2=0 के मूल α तथा β हैं, तो n का न्यूनतम मान, जिसके लिए (αβ)n=1 है
03:46View SolutionIf αandβ are roots of the equation x2+px+2=0 and 1αand1β are the roots of the equation 2x2+2qx+1=0, then (α−1α)(β−1β)(α+1β)(β+1α) is equal to :
05:39View Solutionयदि α,β समीकरण x2−3x+1=0 के मूल, हो तो वह समीकरण जिसके 1α−2,1β−2 मूल है, होगी।
03:16View Solutionयदि α,β,γ समीकरण x3−3x2+3x+7=0 के मूल है, एवम् w3=1: तो α−1β−1+β−1γ−1+γ−1α−1 का मान है।
02:50View Solutionयदि समीकरण ax2+bx+c=0 के मूल α व βहै तब αaβ+b+βaα+b बराबर है
06:08View Solutionयदि समीकरण x2−bxax−c=λ−1λ+1 के मूल α व β इस प्रकार है कि α+β=0 तब λ का मान है
06:06View Solutionयदि α,β समीकरणax2+bx+c=0 के मूल हों , तबlimx→α1−cos(ax2+bx+c)(x−α)2 का मान है
02:27View Solution

