यदि बहुपद 2x3+x2−5x+2 के शून्यक α,β,γ हो तो αβ+βγ+γα का मान होगा
−4
−52
14
−14
The correct Answer is:B
Step by step video, text & image solution for यदि बहुपद 2x^(3)+x^(2)-5x+2 के शून्यक alpha, beta, gamma हो तो alpha beta+beta gamma+gamma alpha का मान होगा by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- बहुपद BOOK - KC SINHACHAPTER - बहुपद EXERCISE - उदाहरण
52 Videos
- बहुपद BOOK - KC SINHACHAPTER - बहुपद EXERCISE - अभ्यास 2.1
18 Videos
- बहुपद BOOK - KC SINHACHAPTER - बहुपद EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
- प्रायिकता या सम्भावितBOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - वस्तुनिष्ठ प्रश्न
54 Videos
- रचनाएँ BOOK - KC SINHACHAPTER - रचनाएँ EXERCISE - अभ्यास 11.1
14 Videos
Similar Questions
निचे दिया गया बहुपद के आलेख को देखकर बतायें कि ये एक-घातीय है या द्विघातीय है अथवा न एक-घातीय है और न द्विघातीय |
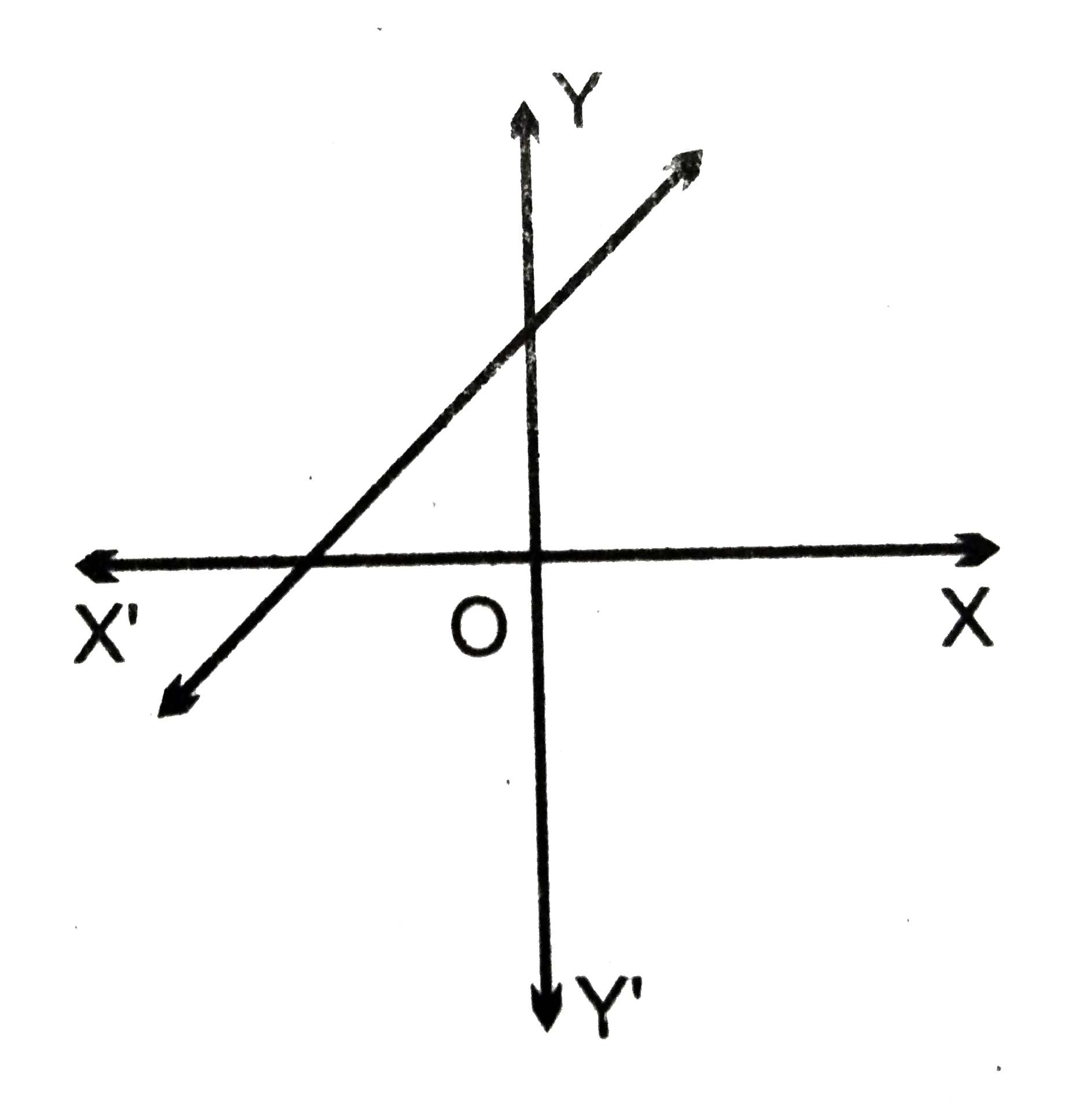
View Solutionनीचे दिया गया बहुपद के आलेख को देखकर जाँच करें कि यह एक घातीय है या द्विघातीय या न तो एक घातीय है और न द्विघातीय |
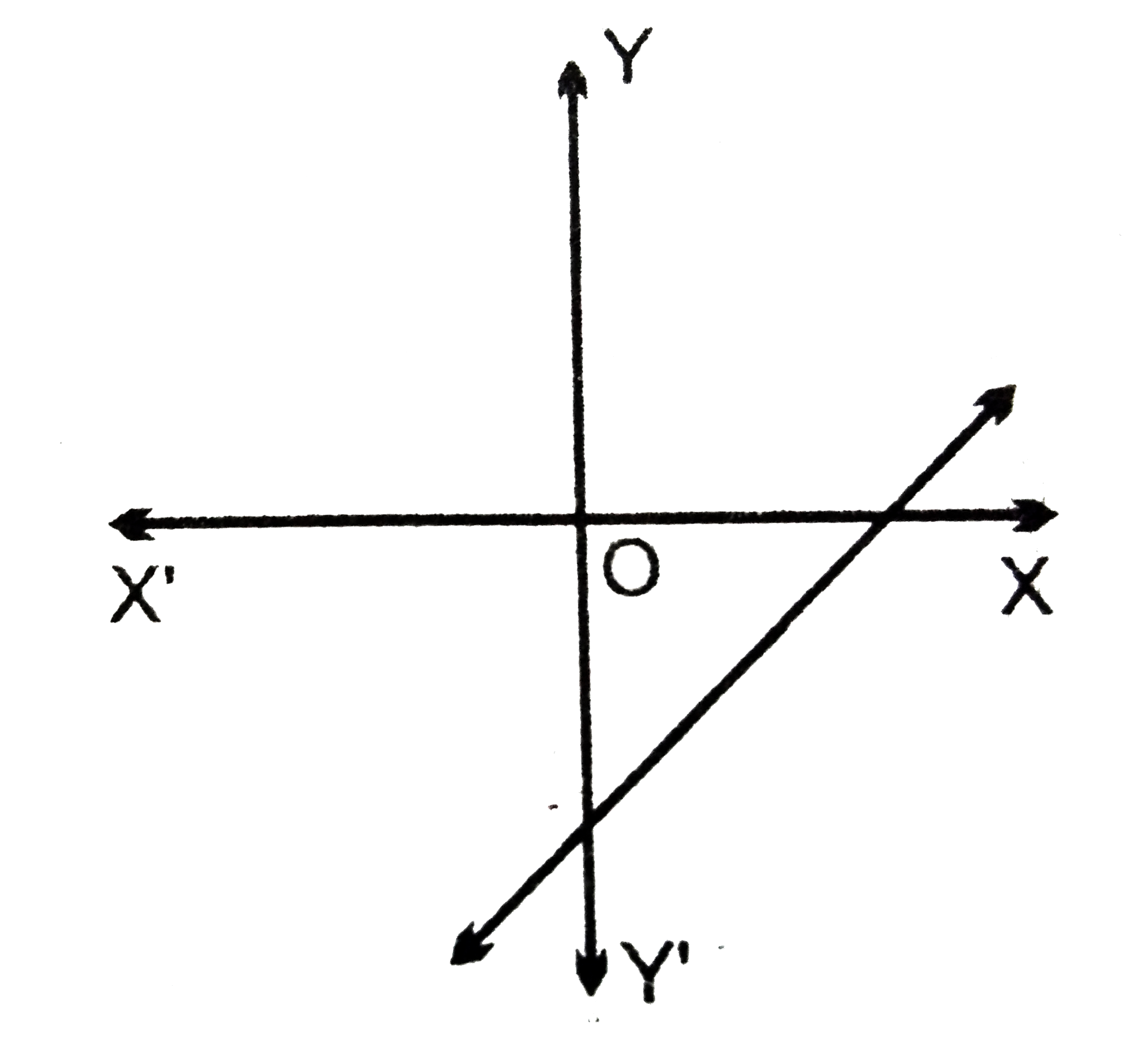
View Solutionयदि p(x)=x3+kx2+hx+6और x+1 तथा x−2,p(x) के गुणनखण्ड है तो h और k का मान ज्ञात करे।
View Solutionदो सिक्के उछालने में दो पट आने के प्रायिकता है:
View Solution5.6 cm लम्बा एक रेखाखण्ड खींचे और इसे 5:8 के अनुपात में अतः विभक्त करें | दोनों भागो को मापे |
View SolutionProve that |[alpha,beta,gamma] ,[alpha^2,beta^2,gamma^2] , [beta+gamma, gamma+alpha, beta+alpha]| = (alpha-beta)(beta-gamma)(gamma-alpha)(alpha+beta+gamma)
View SolutionProve that: ∣∣αβγα2β2γ2β+γγ+αα+β∣∣=(α−β)(β−γ)(γ−α)(α+β+γ) .
View Solutionसाबित करे कि
∣∣ ∣ ∣∣αβγα2β2γ2β+γγ+αα+β∣∣ ∣ ∣∣=(β−γ)(γ−α)(α−β)(α+β+γ).
View Solutionयदि बहुपद 2x3+x2−5x+2 के शून्यक α,β,γ हो तो αβ+βγ+γα का मान होगा
View SolutionProve that, ∣∣ ∣ ∣∣αβγα2β2γ2β+γγ+αα+β∣∣ ∣ ∣∣=(α−β)(β−γ)(γ−α)(α+β+γ)
View Solutionপ্রমাণ করো যে, ∣∣ ∣ ∣∣αβγα2β2γ2β+γγ+αα+β∣∣ ∣ ∣∣=(α−β)(β−γ)(γ−α)(α+β+γ)
View Solutionयदि α,βγ, समीकरण ax3+bx3+c=0 के मूल है | तो सारणिक ∣∣ ∣ ∣∣αββγγαβγγααβγααββγ∣∣ ∣ ∣∣ का मान होगा |
View Solutionयदि बहुपद f(x)=16x2+4x−5के शून्यक α और βहो तो 1α+1βका मान होगा :
View SolutionUsing properties of determinants prove that :
∣∣(α,α2,β+γ),(β,β2,γ+α),(γ,γ2,α+β)|}=(β−γ)(γ−α)(α−β)(α+β+γ)
View SolutionUsing properties of determinants. Prove that∣∣ ∣ ∣∣αα2β+γββ2γ+αγγ2α+β∣∣ ∣ ∣∣=(β−γ)(γ−α)(α−β)(α+β+γ)
View Solution
