ऊँची ध्वज दंड पर एक ऊर्ध्वाधर मीनार एक समकोण बनाती है। यदि उनके बीच की दुरी है , तो मीनार की ऊंचाई ज्ञात करे।
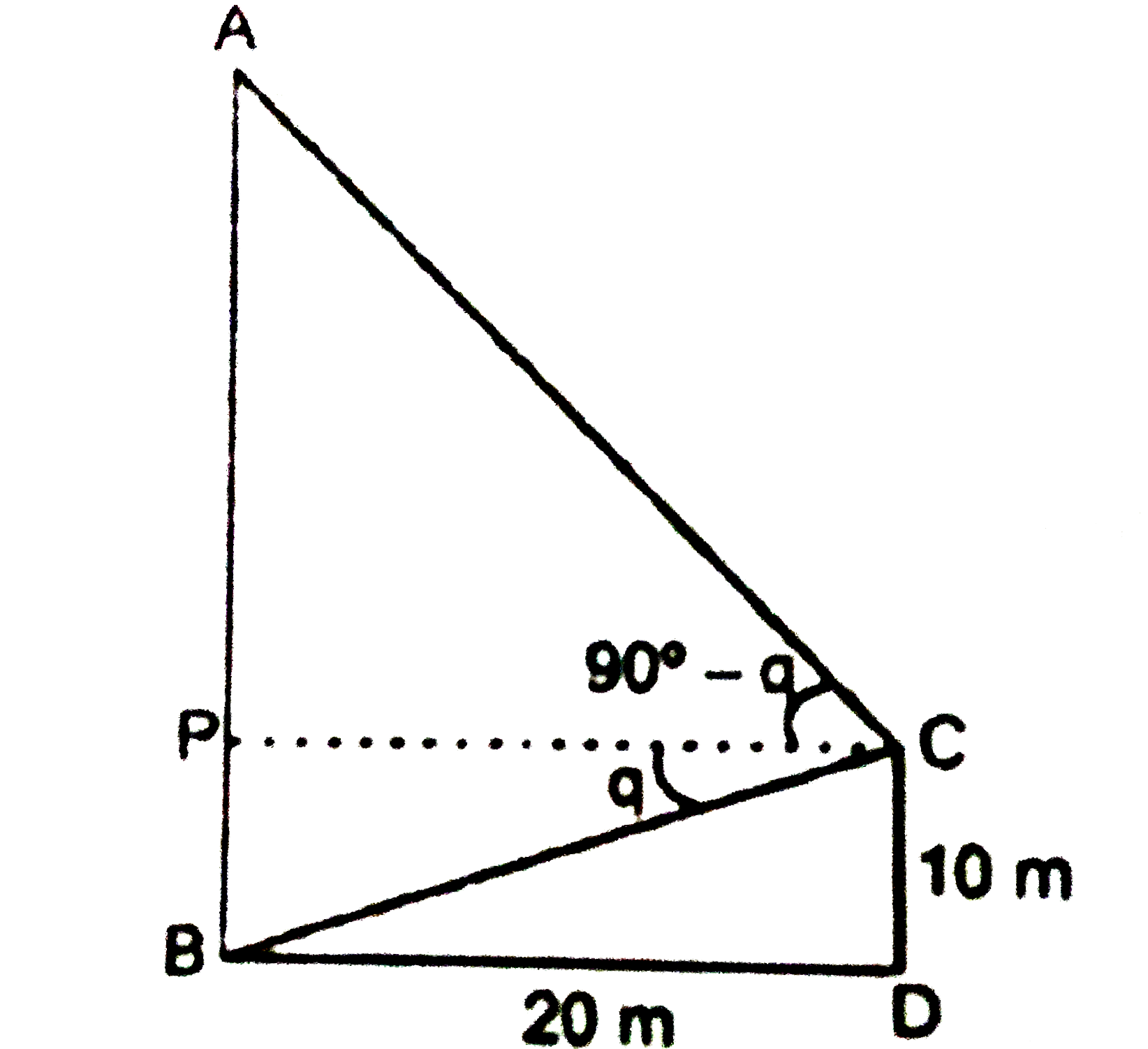
माना की AB, मीनार है CD और ध्वज दंड खींचा
प्रश्नानुसार
समकोण , में,
पुनः समकोण में ,
या
या [ चूँकि समकोण में ]
या
या
या
या
या 20 AB = 1000
या
अतः मीनार की ऊँचाई = 50 m
दूसरी विधि : माना की AB = h m
दिया है ,CD = 10 m तथा BD = 20 ,
C से हम खींचा |
माना की
स्पष्टतः PB = CD = 10 m , PC = BD = 20 m
समकोण में ,
समकोण में ,
या या
या
अतः मीनार की ऊँचाई = 50 m ,
तीसरी विधि : ज्यामिति से
समकोण में ,
या
या m
अतः मीनार की ऊँचाई
Topper's Solved these Questions
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - KC SINHACHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - अतिलघु उत्तरीय प्रश्न
4 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - KC SINHACHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - लघु उत्तरीय प्रश्न
33 Videos
- 2018 BBOOK - KC SINHACHAPTER - 2018 BEXERCISE - प्रश्न
32 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
Similar Questions
△ABC में ∠A=90∘ , AB=12cm और AC=4√3cm, तब ∠B ज्ञात करे।
View Solution△ABC एक समकोण त्रिभुज है जिसमे AB=8 m , ∠BCA=30∘ तब ज्ञात करे :
(i) C से A का उन्नयन कोण ।
(ii) A से C का अवनयन कोण ।
(iii) BC और AB
View Solutionयूक्लिड विभाजन एल्गोरिदम की मदद 870 तथा 225 का महत्तम समावर्तक निकालें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक अनभिनत पास को 6 बार उछाला जाता है। यदि एक समसंख्या प्राप्त करना एक सफलता है , तो
अधिक - से - अधिक 5 सफलताओ की प्रायिकता ज्ञात कीजिए।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionसूर्य और पृथ्वी के बीच की दूरी 1.496×108 km है तथा पृथ्वी और चंद्रमा के बीच की दूरी 3.84×108m है सूर्य ग्रहण होने पर चन्द्रमा पृथ्वी और सूर्य के बीच में आ जाता है इस विशेष समय पर सूर्य और चंद्रमा के बीच की दूरी क्या है ?
View Solutionएक रेखा की दिक्-कोसाइन ज्ञात कीजिए तो निर्देशांक्षो के साथ समान कोण बनाती है |
View SolutionA vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angle of elevation of the bottom of the flag staff is alpha and that of the top of the flag staff is beta . then the height of the tower is एक ऊर्ध्वाधर मीनार एक क्षेतिज समतल पर खड़ी है और उसके ऊपर 1 ऊँचाई का ऊर्ध्वाधर ध्वजखण्ड लगा है। समतल पर एक बिन्दु पर ध्वजदण्ड के तल का उन्नयन कोण alpha है और ध्वजदण्ड के शीर्ष भाग का beta है। मीनार की ऊँचाई बताइए ?
View SolutionThe length of a shadow of a vertical tower is 1/sqrt3 times of its height. The angle of elevation of the Sun is यदि एक ऊर्ध्वाधर मीनार की परछाई की लंबाई उसकी ऊँचाई का 1/sqrt3 गुणा है, तो सूर्य का उन्नयन कोण है-
View SolutionThe base of a pyramid is an equilateral triangle of side is 10m. If the height of the pyramid is 40 sqrt3 m, then the volume of the pyramid is : एक पिरामिड का आधार 10 m भुजा वाला एक समबाह त्रिभुज है। यदि पिरामिड की ऊंचाई 40 sqrt3 मीटर है, तो पिरामिड का आयतन क्या है
View Solution
